3.3 Создание модели адаптивной системы автоматического регулирования

Общепринятый порядок синтеза систем управления состоит в следующем:

– задается математическая модель объекта (на практике это обычно экспериментальная переходная харак­теристика объекта);

– принимается критерий оптимальности системы управления;

– по модели объекта определяются структура и чис­ленные значения параметров алгоритма функциониро­вания контроллера (регулятора), удовлетворяющие принятому критерию оптимальности.

Считается, что если модель достаточно близка к ре­альному объекту, а выбранный метод синтеза и сами расчеты выполнены безукоризненно, то спроектирован­ная система заработает без какой-либо существенной доводки при пуске. Однако опыт свидетельствует о том, что такой оптимистический прогноз, как правило, не оправдывается. Объясняется это двумя причинами:

– системным характером задачи получения математи­ческой модели объекта; это значит, что для формули­ровки критерия приближения последней необходимо располагать алгоритмом функционирования контрол­лера, для определения которого собственно и нужна эта модель [74];

– практической невозможностью учета отклонения принимаемой в расчетах динамической модели кон­троллера от реальной (наличия широтно-импульсного преобразования сигнала на выходе контроллера, зоны нечувствительности, люфтов в механических сочлене­ниях исполнительного механизма и т. п.).

Выход из сложившейся ситуации состоит в том, что системы управления даже относительно стабильными объектами должны проектироваться как адаптивные (с автоматизированной настройкой) [74, 2]. Эффектив­ность таких систем определяется тем, что они оперируют всей системой в целом, причем при соответствующем выборе режима идентификации можно осуществлять автоматическую линеаризацию нелинейности в значительном для каждой конкретной системы диапа­зоне частот и отклонений сигналов [75].

Разработка систем управления должна быть двух­этапной.

1. Выдвижение гипотез о структуре системы и ее ал­горитмах управления и регулирования (в том числе ал­горитмов адаптации), получение начальной (часто эта модель называется априорной) математической модели объекта и расчет по ней оптимальных параметров на­стройки выбранных алгоритмов с последующей провер­кой их работоспособности на имитационных моделях.

2. Окончательная адаптация с помощью специали­зированных сервисных алгоритмов полученной на пре­дыдущем этапе системы к реальным условиям работы на действующем объекте при вводе ее в эксплуатацию. Алгоритмы адаптации включаются в состав общего ал­горитмического обеспечения системы и остаются в ра­боте на весь период ее эксплуатации, поскольку свой­ства элементов системы могут меняться во времени.

В функции адаптации не входит подстройка параметров регуляторов к относительно быстро меняющимся свойствам объекта, вызванным контролируемыми возмущениями, прежде всего – изменениями нагрузки объекта. В этом случае должна применяться обычная коррекция настройки регуляторов по заранее заданным законам, реализуемым в соответствующих корректирующих блоках. Однако в функции адаптации входит настройка этих корректирующих блоков. Вообще возможности теории автоматического управления (как и любой другой теории) ограничены некоторыми пределами. При слишком быстрых изменениях свойств объекта и связанным с этим появлением нелинейных эффектов принципиальная возможность адаптации систем управления достаточно сложными в динамиче­ском отношении объектами оказывается весьма проблематичной.

Обычно структура адаптивной системы управления представляется такой, как показана на рис. 8: к контуру регулирования, состоящему из объекта Об и регулятора Рег, подсоединяются адаптирующее устройство Ад, на вход которого подаются входной (t) и выходной y(t) сигналы объекта. В идентифицирующем устройстве Ид по этим сигналам оценивается модель объекта, а в вычислительном устройстве ВУ рассчитываются оптимальные па­раметры настройки регулятора, которые затем устанавливаются с помощью адаптирующего воздействия a(t).

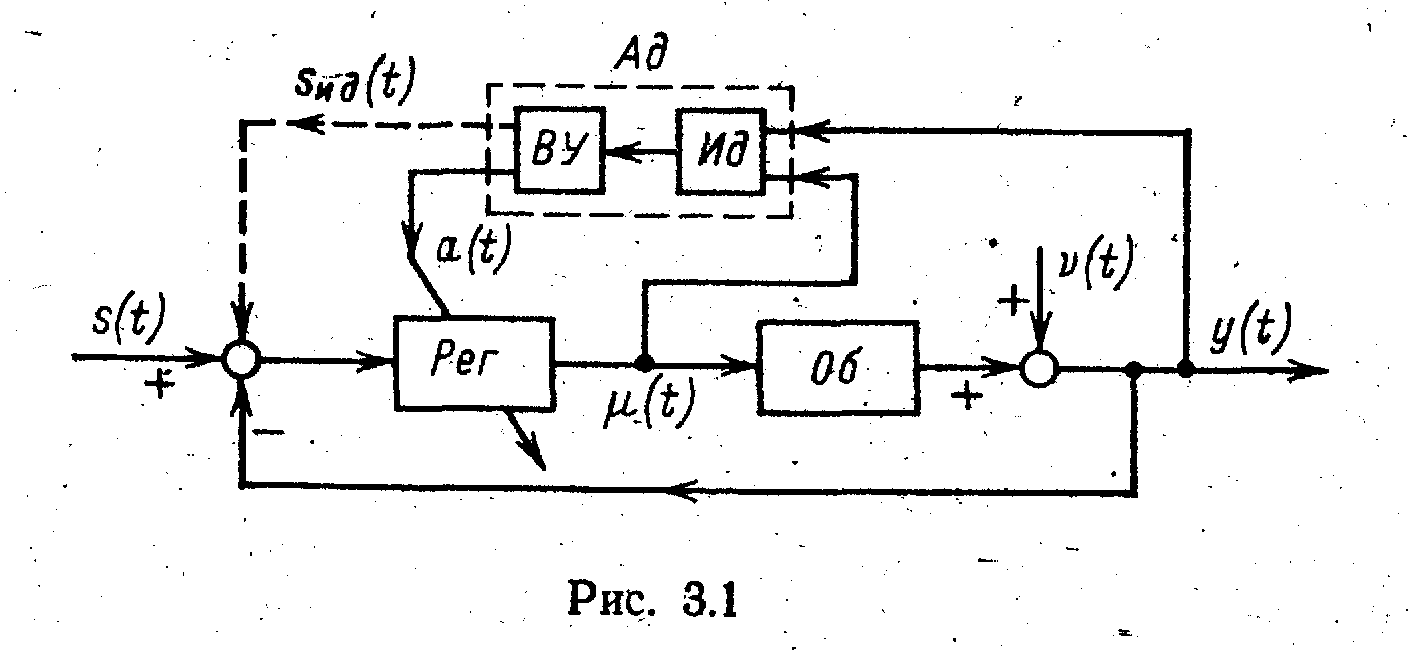
Рис. 8. Структура адаптивной системы

Процесс адаптации должен сопровождаться идентификацией объектов, что в большинстве случаев принципиально невозможно осуществить по условиям нормальной эксплуатации. Поэтому приходится использовать активный эксперимент, сопровождаемый подачей на объект специальных идентифицирующих воздействий. Такими воздействиями могут быть [2]:

– специально организованное возмущение или изменение заданного значения регулируемой величины;

– изменение алгоритма функционирования регулятора;

– изменение структуры системы регулирования.

Далее будет рассмотрен метод адаптации, исполь­зующий сигнальное гармоническое идентифицирующее воздействие. Достоинством такого метода являет­ся возможность обоснованного применения методов математической статистики в процессе проведения итерационной процедуры движения к оптимуму [8]. Практическая значимость этого обстоятельства состо­ит в возможности уменьшения амплитуды воздействий до приемлемого уровня и, несмотря на это, получения удовлетворительных оценок параметров выходных ко­лебаний благодаря увеличению продолжительности адаптации.

Пассивное наблюдение за поведением объекта в процессе нормального функционирования не приводит к успеху.

Объясняется это тем, что поскольку объект находится в составе системы, то и оперировать следует с воздействиями, являющимися входными сигналами всей системы; при этом входной сигнал следует выбрать таким образом, чтобы идентифицируемый канал системы зависел только от одного неизвестного оператора объекта.

Организация процесса оценки модели объекта, структура адап­тивной системы управления, приведенная на рис. 8, должна быть дополнена еще одним, идентифицирующим воздействием, которое должно оказывать адаптирующее устройство Ад на систему с целью идентификации объек­та. На рис. 8 воздействие s_ид(t) показано пунктирной стрелкой в виде сигнального воздействия, подаваемого на задатчик регулятора. Однако такое идентифицирующее воздействие не обязательно должно быть сигнальным. Оно может быть также параметрическим, алгоритмическим, структурным.

Чаще всего автоматическая настройка осуществляется путем включения в канал сигнала ошибки двухпозиционного реле с малым выходным сигналом. Далее по параметрам автоколебаний, возникающих в замкнутой системе, определяются требуемые настройки ПИД-регулятора. В то же время при таком способе самонастройки происходит прекращение процесса регулирования объекта на время настройки, наблюдается высокая чувствительность к шумам в канале измерения, возникает опасность срыва автоколебаний при действии возмущений.

Существует алгоритм настройки ПИД-регулятора в замкнутом контуре путем подачи на вход системы пробного синусоидального сигнала. Однако для этого алгоритма требуется достаточно большое время настройки (около восьми, десяти периодов колебаний на резонансной частоте замкнутой системы).

В данной работе используется метод Циглера - Никольса с частотным разделением каналов управления и самонастройки, что достигается включением двух заграждающих цифровых фильтров в обратную связь контура регулирования.

Для повышения быстродействия процесса самонастройки предлагается работать на первом, начальном этапе самонастройки на двух частотах пробного сигнала, одна из которых больше критической частоты объекта управления. Возможность работы блока адаптации на частотах, больших критической частоты, объясняется тем, что для объектов с запазды­ванием увеличение частоты пробных колебаний сопровождается значительно меньшим снижением амплитуды выходной гармоники по сравнению с объектами без запаздывания.

На рис. 9 приведена структурная схема такой адаптивной системы управления. Основной контур системы состоит из настраиваемого регулятора Р, собственной объекта управления ОУ и двух заградительных фильтров (основного ЗФО и дополнительного ЗФД). Дополнительный фильтр с помощью переключателя П₁ включается лишь на первом этапе либо периодически для определения требуемых по методу Циглера – Никольса настроек. Блоки синхронного детектирования СД₁, СД₂ вычисляют установившиеся значения амплитуд А_б, А₀ и фаз Ф_б, Ф₀ пробных составляющих в выходных сигналах основного заграждающего фильтра у₁ и объекта управления у. Отслеживание заданного фазового сдвига осуществляется с помощью блока фазовой автоподстройки частоты БФАЧ. Путем сравнения установившегося значения фазового сдвига Ф₀ с заданным Ф_з блок корректирует частоты пробных синусоидальных колебаний первого Г₁ и второго Г₂ генераторов. Причем частота генератора Г₂ выбрана вдвое выше частоты генератора Г₁. Вычислительные блоки ВБ₁, ВБ₂, ВБ₃ по командам блока управления БУ проводят вычисления поправочного коэффициента С, параметров настройки регулятора и коэффициентов заграждающих фильтров. В запоминающих устройствах ЗУ₁, ЗУ₂ хранятся значения коэффициента С и фазового сдвига Ф₀ в объекте управления в момент расчета требуемых настроек. По командам блока управления с помощью переключателей П₃, П₄, П₅, П₆ происходит коммутация входных сигналов соответствующих блоков на разных этапах работы системы.

Рис. 9. Структурная схема разрабатываемой адаптивной системы автоматического управления

Процесс самонастройки состоит из двух этапов: двухчастотного, в конце которого вычисляются требуемые настройки и коэффициент С; основного, в котором процесс самонастройки происходит уже на одной повышенной частоте пробных колебаний с одним заграждающим фильтром ЗФО в контуре обратной связи. Именно определение критической частоты и соответствующей ей амплитуды колебаний для блока ОУ+ЗФО позволяет работать с нужными параметрами настроек на втором этапе. Достигается это с помощью поправочного коэффициента С, устанавливающего связь между требуемыми по методу Циглера – Никольса настройками на первом и втором этапах работы системы.

Результаты данного раздела использованы в хоздоговоре №11/02 ТУСУРа с ЗАО «ЭлеСИ» (П.1).