4.2.6 Выбор метода расчета

Описав наиболее распространенные методы расчета параметров настройки регуляторов, отдадим предпочтение методу расширенных амплитудно-фазо-частотных характеристик, т.к. исходные данные получены экспериментальным методом. Метод РАФЧХ позволяет достаточно точно определить параметры настройки регуляторов. Одним из существенных его достоинств, является то что метод наиболее оптимальным с точки зрения предъявляемых требований технологическим процессом к переходным характеристикам в промышленных системах.

4.2.7 Расчет оптимальных параметров настройки пи-регулятора

Структурная схема системы автоматического регулирования температуры горячего дутья доменной печи представлена на рис. 33.

Рис. 33. Структурная схема системы автоматического регулирования

Для дальнейших расчетов используем многофункциональную интегрированную систему автоматизации математических и научно-технических расчетов MATLAB 5.3.1 и пакет ее расширения Control System Toolbox, разработанные фирмой The MatWorks Incorporated (www.mathworks.com).

С помощью разработанной программы в среде MATLAB (П. 5) построены частотные характеристики объекта управления, рассчитаные по методу РАФЧХ, изложенному выше, область оптимальных параметров настройки ПИ- регулятора, построен переходный процесс замкнутой системы автоматического регулирования температуры горячего дутья доменной печи и произведена его оценка качества.

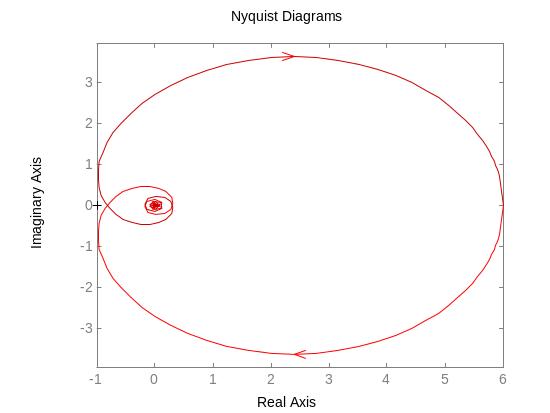
Рис. 34. АФЧХ объекта управления

K_p

K_p/T_и

Рис. 35. Область оптимальных параметров настройки ПИ-регулятора

Точка на графике, соответствующая максимуму (т.е. минимуму первого интегрального критерия), определит параметры настройки ПИ-регулятора К_p = 0,47; Т_и = 49,6 с.

Тогда передаточную функцию ПИ-регулятора можно записать в следующем виде:

.

Рис. 36. Переходный процесс в замкнутой системе регулирования

Любая промышленная АСР кроме устойчивости должна обеспечивать определенные качественные показатели процесса регулирования.

Качество процесса регулирования оценивают по переходной характеристике по отношению к единичному ступенчатому возмущающему воздействию.

Склонность системы к колебаниям, а следовательно, и запас устойчивости могут быть охарактеризованы максимальным значением регулируемой величины h_max или так называемым перерегулированием:

 = A₃/A₁100% = 20,338%.

Время регулирования t_p – время, по истечении которого отклонение регулируемой величины от установившегося состояния не будет превышать некоторой наперед заданной величины . Обычно  = 0,05y() = 0,051 = 0,05.

t_p = 200 c.

Максимальная динамическая ошибка

А₁ = 0,212.

Степень затухания называется отношение разности двух соседних амплитуд, одного знака, к большей из них:

 = (A₁ – A₂)/A₁  0,96.

Результаты данного раздела опубликованы в [112, 115].

4.3 Расчет оптимальных параметров настройки адаптивной системы автоматического регулирования

В теории автоматического управления разработаны различные методы расчета АСР при заданных критериях качества, а также методы оценки качества переходных процессов при заданных параметрах объекта и регулятора. При этом наряду с точными методами, требующими больших затрат времени и ручного труда, разработаны приближенные методы, позволяющие сравнительно быстро оценить рабочие параметры регулятора или качество переходных процессов (метод Циглера – Никольса для расчета настроек регуляторов; приближенные формулы для оценки интегрального квадратичного критерия и т.п.).

При определении настроек регуляторов в качестве показателя оптимальности системы регулирования обычно выбирают интегральный критерий качества (например, интегральный квадратичный критерий) при действии на объект наиболее тяже­лого возмущения с учетом добавочного ограничения на запас устойчивости системы. В практических расчетах запас устойчивости удобно характеризовать показателем колебательности системы; его значение для систем, имеющих интегральную составляющую в законе регулирования, определяется максимумом амплитудно-частотной характеристики замкнутой системы регулирования.

В дальнейшем под оптимальными будем понимать настройки регулятора, обеспечивающие заданную степень колебательности m процесса регулирования при минимуме интегрального квадратичного критерия J_кв.

Среди инженерных методов расчета настроек регуляторов одни являются более точными, но трудоемкими для ручного счета, другие – простыми, но приближенными. Наиболее распространенными способами, отражающими методику точного и приближенного расчета настроек, яв­ляются метод расширенных амплитудно-фазовых частотных характеристик (РАФЧХ) и метод незатухающих колебаний (Циглера – Никольса).

Метод незатухающих колебаний (Циглера—Никольса). В соответствии с этим методом расчет настроек ПИ- или ПИД-регуляторов проводят в два этапа: 1—расчет критической настройки пропорциональной составляющей S₁^кр(S₀ = S₂ = 0), при которой АСР будет находиться на границе устойчивости, и соответствующей ей _кр; 2 – определение по S₁^кр и _кр оптимальных настроек S₁*, S₀*, S₂*, обеспечивающих степень затухания   0,8 – 0,9.

Уравнения для расчета S₁^кр и соответствующей ей частоты при т = 0:

_об() +  = 0; S₁^кр = [A_об(_кр)] ^–1.

Оптимальные настройки ПИ- и ПИД-регуляторов находят по следующим формулам:

для П-регулятора

S₁* = 0,5S₁^кр;

для ПИ-регулятора

S₁* = 0,45S₁^кр;

S₀*/S₁* = 0,19_кр или S₀* = 0,086S₁^кр_кр;

для ПИД-регулятора

S₁* = 0,6S₁^кр;

S₀*/S₁* = 0,32_кр или S₀* = 0,192S₁^кр_кр;

S₂*/S₁* = 0,785/_кр или S₂* = 0,471S₁^кр/_кр.

Метод Циглера – Никольса лежит в основе многих методов настройки дискретных ПИД-регуляторов. В частности, если рекуррентный алгоритм управления, соответствующий аналоговому ПИД-закону, имеет вид

,

то для больших значений периода квантования t₀ параметры настройки K₁*, K₀*, K₂* могут быть найдены по следующим формулам:

для П-регулятора

K₁* = 0,5 K₁^кр;

для ПИ-регулятора

K₁* = 0,45 K₁^кр – 0,5 K₀*;

K₀* = 0,54 K₁^крt₀/T_кр, если   0,25t₀;

для ПИД-регулятора

K₁* = 0,6 K₁^кр – 0,5 K₀*;

K₀* = 1,2 K₁^крt₀/T_кр, если   0,25t₀;

K₂* = 3/40 K₁^кр T_кр/t₀.

В приведенных уравнениях K₁^кр и T_кр – коэффициент при П-составляющей закона управления и период колебаний выходной координаты, соответствующие режиму незатухающих колебаний АСР.

Опишем процесс самонастройки в созданной модели адаптивной системы автоматического управления (П. 6).

Первый этап. Все переключатели находятся в первом положении. В регуляторе устанавливаются настройки, гарантирующие устойчивость замкнутой системы с двумя заграждающими фильтрами: К_р = 0,7; Т_и = 60 с. В генераторы синусоидальных колебаний Г₁, Г₂ вводятся начальные значения амплитуд а₁, а₂ и периодов Р₁, Р₂ колебаний. Нормированный период колебаний низкочастотного генератора Г₁ был принят Р₁ = 28, а генератора Г₂ – соответственно вдвое меньше, т.е. Р₂ = 14. Амплитуда генератора Г₁ а₁ = 5%, а генератора Г₂ выбрана вдвое больше, т.е. а₂ = 10%. Таким образом, генератор Г₁ является ведущим, а Г₂ – ведомым, для которого двукратное соотношение амплитуд и частот сохраняется на протяжении всего этапа работы системы.

Сигнал задания для блоков фазовой автоподстройки частоты с помощью переключателя П₅ устанавливается в соответствии с методом Циглера – Никольса на уровне Ф_з = –.

После проведения таких подготовительных операций в работу включаются генераторы синусоидальных колебаний, и блок фазовой автоподстройки частоты путем изменения нормированного периода колебаний Р₁ начинает отслеживать заданный фазовый сдвиг.

В конце первого этапа для нормированных периодов колебаний Р₁ = 36 и Р₂ = 18 установившееся значение фазового сдвига и амплитуды для низкочастотной составляющей в сигнале у₁ приняли следующие значения: Ф_б = –3,146 рад, А_б = 4,2453% и соответственно Ф₀ = –4,2 рад, А₀ = 3,859% для высокочастотной составляющей в сигнале у.

По этим значениям с помощью вычислительного блока 1 рассчитывается поправочный коэффициент С = А_ба₂/(А₀а₁) и требуемые по методу Циглера – Никольса настройки ПИ-регулятора:

К_р = 0,45а₁/А_б; Т_и = Р₁/0,5.

В данном случае С = 2,2; К_р = 0,53; Т_и = 72. Таким образом, критерием окончания первого этапа является достижение фазой Ф_б установившегося значения, близкого к –.

Второй этап. По команде блока управления проводятся следующие операции: вычисленные настройки вводятся в регулятор Р; поправочный коэффициент С запоминается в ЗУ₁; отключается низкочастотный генератор Г₁ и синхронный детектор СД₁; в высокочастотном генераторе Г₂ сохраняются нормированный период и амплитуда, соответствующая концу первого этапа; в ЗУ₂ запоминается значение фазового сдвига в ОУ; все переключатели устанавливаются в положение 2. Система продолжает работу, непрерывно удерживая с помощью синхронного детектора СД₂ и блока ФАЧ значение фазового сдвига на уровне Ф₀ = –4,2 рад на повышенной частоте пробных колебаний. Настройки регулятора корректируются периодически, через каждые два периода колебаний генератора. Расчет настроек на этом этапе производится по формулам

К_р = 0,45а₂/(А₀С); Т_и = Р₂/0,25.

Отсюда видно, что наличие поправочного коэффициента позволяет оставаться на требуемом уровне.

Построим переходные процессы по каналам задающего воздействия (рис. 37) и возмущения, идущего со стороны регулирующего органа (рис. 38). Переходные процессы построены при настройках регулятора, обеспечивающих устойчивость замкнутой системы (t < 700 c), и при настройках, полученных в процессе адаптации (t  700 c).

h(t), ^oC

t, c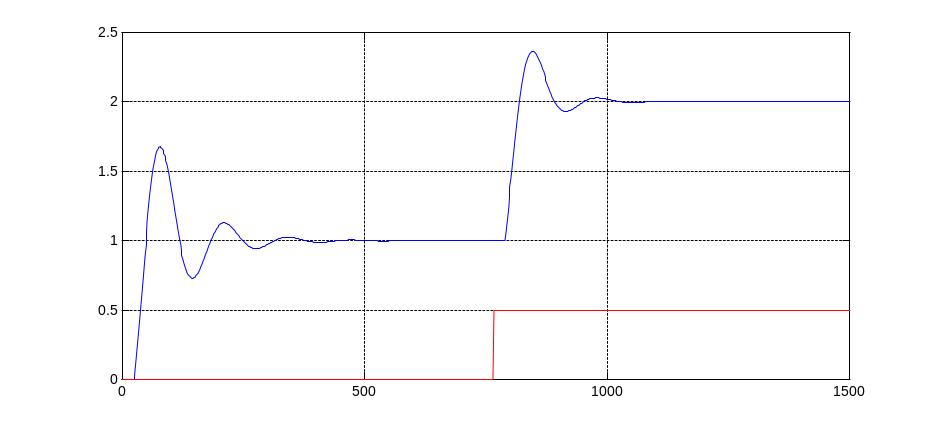

Рис. 37. Переходный процесс в адаптивной системе автоматического регулирования по каналу задающего воздействия

t, c

h(t), ^oC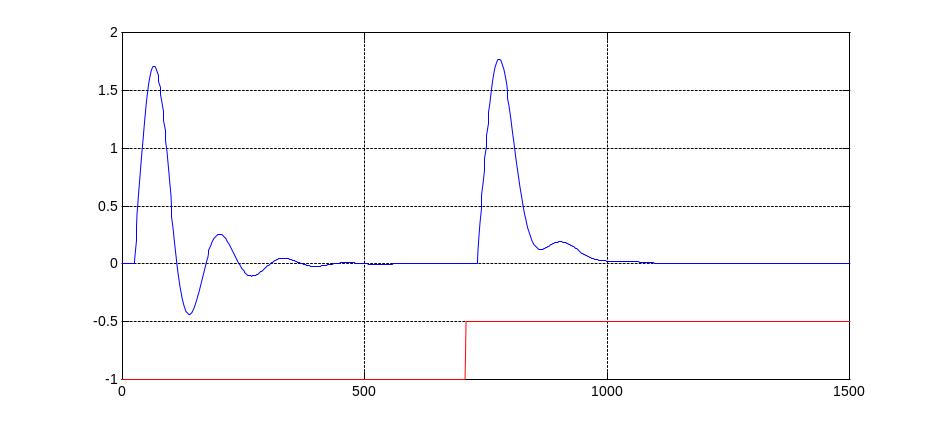

Рис. 38. Переходный процесс в адаптивной системе автоматического регулирования по каналу возмущения, идущего со стороны регулирующего органа

Оценим качество переходного процесса, полученного после процесса адаптации.

Перерегулирование:

 = A₃/A₁100% = 18,5%.

Время регулирования:

t_p = 203 c.

Максимальная динамическая ошибка:

А₁ = 0,32.

Степень затухания:

 = (A₁ – A₂)/A₁  0,95.

Следует заметить, что при изменении коэффициента усиления объекта поправочный коэффициент С остается постоянным. Необходимость повторения первого этапа с целью уточнения значения коэффициента С возникает только при значительных (в 2 раза и более) изменениях постоянных времени и запаздывания в объекте (табл. 7). В этой таблице приведены значения параметров настройки ПИ-регулятора по методу Циглера – Никольса для объекта управления при двукратном изменении относительно номинала (97,7 с) его постоянной времени Т (48,85 и 195,4 с) и значения параметров настройки при тех же вариациях постоянной времени Т на втором этапе самонастройки при фиксированном значении поправочного коэффициента С = 2,2.

Как видно из табл. 7, уход настроек от расчетных значений весьма незначительный и составляет не более 16% по коэффициенту усиления регулятора.

Таблица 7

Значения параметров настройки регулятора при вариации параметров объекта управления

Постоянная времени Т, с	Значения параметров настройки по методу Циглера – Никольса		Значения параметров настройки на втором этапе
	Кр	Ти	Кр	Ти
48,85	0,295	67	0,362	69,1
195,4	1,014	75,83	1,12	72,5