3.5 Разработка элементов устройств управления на основе многофункциональных логических модулей

Одним из весьма перспективных и быстропрогрессирующих направлений в области построения и синтеза цифровых устройств управления является разработка их внутренней структуры. Определенный интерес представляют логические элементы, функциональные возможности которых значительно расширяются за счет переключения имеющихся в них блоков. Это переключение может осуществляться настройкой элемента либо комбинацией соединений выходов. Особенность синтеза устройств управления на основе проблемно-ориентированных быстрых интегральных схем (БИС) состоит в том, что средством реализации алгоритмов функционирования проектируемых устройств управления, либо систем являются многофункциональные логические модули (МЛМ), которые могут настраиваться на реализацию любого конкретного логического алгоритма из заданного класса булевых формул. Таким образом происходит реализация автоматного принципа обработки информации. Последнее определяет структурно сближение модулей обработки информации и управления. Данное направление предполагает модульный принцип построения систем управления на основе принципов многофункциональности и регулярности. Отличной особенностью данного направления является развитие элементной базы проектируемых устройств на основе теории многофункциональных автоматов [57].

Уже первые результаты применения теории многофункциональных автоматов при разработки элементной базы для всевозможных устройств управления и компьютеров показали неоспоримые преимущества данного направления: сокращение типового состава элементной базы; расширение функциональных возможностей элементной базы; уменьшение сложности цифровых систем; сокращение объема резервных комплектов; повышение надежности; возможность создания адаптивных систем.

Согласно проведенным исследованиям [7], основную долю реализуемых в устройствах управления составляют бесповторные булевы формулы – от 93 до 99,7%.

Следовательно, для рассматриваемого класса устройств управления характерно, что описывающие их булевы формулы бесповторны или близки к ним. Таким образом, из результатов проведенного исследования вытекает, что МЛМ для построения управляющих логических устройств, исходя из специфики булевых формул, описывающих алгоритмы их функционирования, должны быть способны реализовать путем настройки не произвольные функции n переменных, а лишь только те из них, для которых булевы формулы бесповторны или обладают малой повторностью переменных, что обеспечивает построение модулей с малой элементной сложностью и числом внешних выводов.

Из сказанного выше определим классы булевых формул, в свете которых предполагается проводить разработку и проектирование.

В настоящее время различают два больших класса булевых функций – бесповторные и повторные [7, 71].

Функцию будем называть бесповторной, если каждый аргумент, взятый в прямой или инверсной форме, входит в нее не более одного раза. Во всех остальных случаях функция является повторной.

Бесповторные булевы функции подвергнем дальнейшей классификации (рис. 13).

Если в записи бесповторной булевой функции f(x_i), где i = 1,2,...,n; n – число аргументов, индекс i при логи­ческих аргументах возрастает слева направо, то будем считать, что эта функция упорядочена. Упорядоченной будем считать функцию и в том случае, если существуют тождественные преобразования, в резуль­тате которых получается запись формулы с возрастающими слева нап­раво индексами аргументов. Если в записи бесповторной булевой функции аргументы с теми или иными индексами отсутствуют, то будем счи­тать, что эта функция содержит пропуски соответствующих аргументов, и назовем ее функцией с пропусками аргументов. С пропусками аргу­ментов будем считать и такие бесповторные булевы функции, для которых  < n, где  – максимальный индекс при логическом аргументе.

Пример 1. Функция зависит от аргументов А₁, А₂, А₃, А₄, является упорядоченной, представлена в дизъюнктивно нормальной форме (ДНФ) и не содержит пропусков аргументов.

Пример 2. Функция

зависит от аргументов А₁, А₂, А₃, А₄, является упорядоченной, представлена в конъюнктивно нормальной форме (КНФ) и не имеет пропусков аргументов.

Пример 3. Функция

зависит от аргументов А₁, А₂, А₃, А₄, А₅, представлена в форме четвёртого порядка, является упорядоченной и не содержит пропусков аргументов.

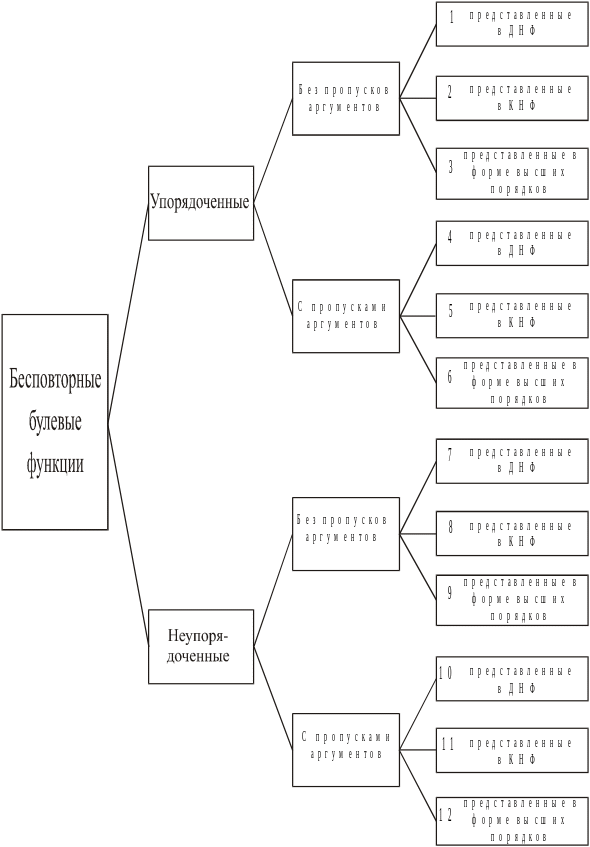
Рис. 13. Классификация бесповторных булевых функций

Пример 4. Функция

f₄ = A₁ + A₃A₄

зависит от аргументов А₁, А₂, А₃, А₄, упорядочена, представле­на в ДНФ с пропуском аргумента А₂.

Пример 5. Функция

зависит от аргументов А₁, А₂, А₃, А₄,...,А₈, является упорядочен­ной, представлена в КНФ с пропуском аргументов А₆, А₇, А₈.

Пример 6. Функция

зависит от аргументов А₁, А₂, А₃, А₄, является неупорядоченной, представлена в ДНФ и не содержит пропусков аргументов.

В дальнейшем будем пользоваться приведенной классификацией и ориентироваться в первую очередь на реализацию бесповторных упорядоченных функций с пропусками аргументов.

Разработанный МЛМ ориентирован на вычисление вышеназванных булевых функций, представленных классами 1 – 6 [116] и подклассом J , определяемым следующим образом. Пусть дана функция, явно или неяв­но зависящая от аргументов x₁, x₂, …, x_n. Запишем эти аргу­менты в порядке возрастания их индексов слева направо. Аргумент, имеющий наименьший индекс, будем называть минимальным, а наиболь­ший – максимальным. Диапазоном функции назовем замкнутый интервал, границы которого образуют индексы минимального и максимального аргументов. Условимся, что интервалы двух различных функций пересе­каются, если минимальный аргумент одной из функций входит в интер­вал другой.

Пусть дана функция, явно или неяв­но зависящая от аргументов x₁, x₂, …, x_n. Запишем эти аргу­менты в порядке возрастания их индексов слева направо. Аргумент, имеющий наименьший индекс, будем называть минимальным, а наиболь­ший – максимальным. Диапазоном функции назовем замкнутый интервал, границы которого образуют индексы минимального и максимального аргументов. Условимся, что интервалы двух различных функций пересе­каются, если минимальный аргумент одной из функций входит в интер­вал другой.

Если функция f представлена в виде

f = l *  *q,

то она входит в подкласс J, где l и  – упорядоченные функ­ции с пересекающимися диапазонами; q – упорядоченная функция, ми­нимальный аргумент которой не входит в диапазон функций l и .

В общем случае функция q может быть тождественно равна нулю; * – знак конъюнкции или дизъюнкции. Функции l и  могут быть любого порядка.

Логическая схема разработанного МЛМ (рис. 14) описывается следующей системой булевых формул:

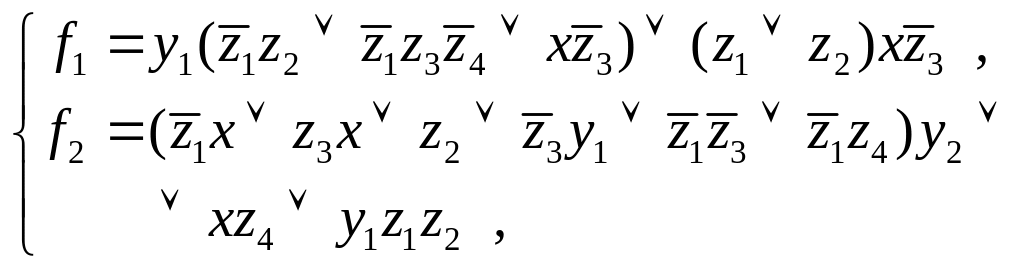
где x, y₁, y₂ – информационные входы; z₁, z₂, z₃, z₄ – наст­роечные входы; f₁, f₂ – выходы МЛМ.

Рис. 14. Ячейка H-структуры

Многофункциональный логический модуль, который в дальнейшем будем называть Н‑ячейкой, реализует следующие системы булевых формул:

1) при z₄ = 0, z₃ = 0, z₂ = 0, z₁ = 0;

2) при z₄ = 0, z₃ = 0, z₂ = 0, z₁ = 1;

1) 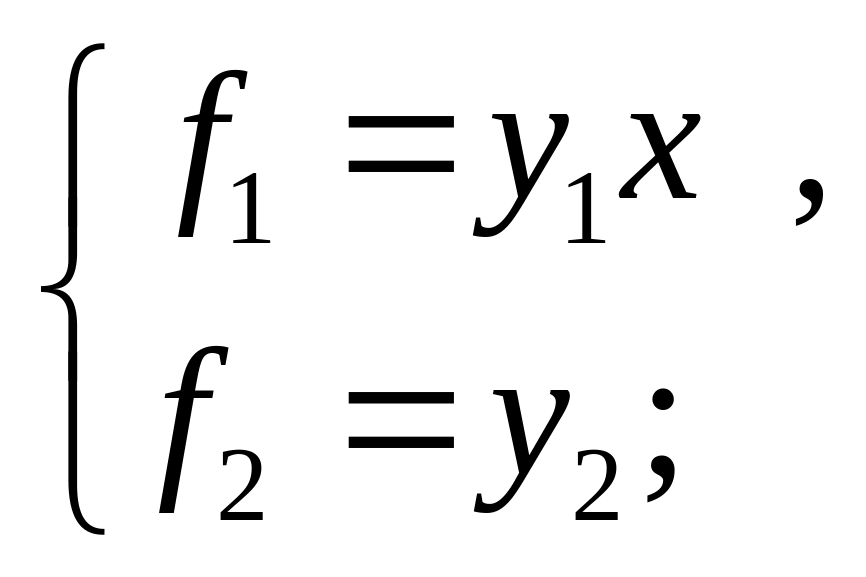(рис. 15, а) 2) (рис. 15, б)

3) при z₄ = 0, z₃ = 0, z₂ = 1, z₁ = 0;

4) при z₄ = 0, z₃ = 0, z₂ = 1, z₁ = 1;

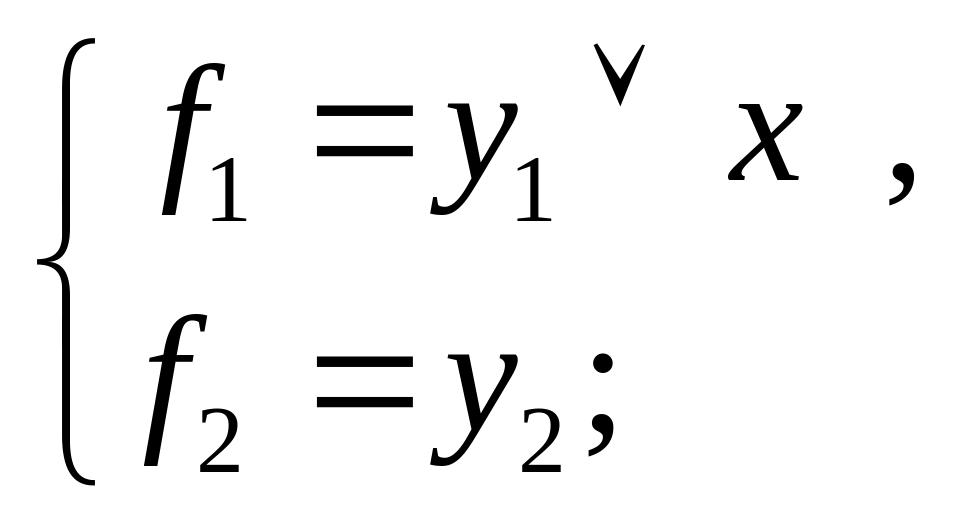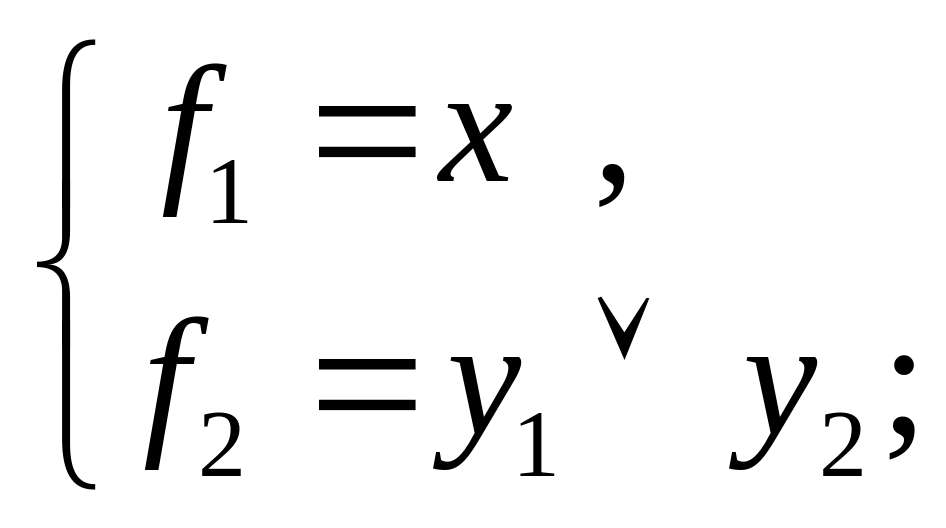3) (рис. 15, в) 4) (рис. 15, г)

5) при z₄ = 0, z₃ = 1, z₂ = 0, z₁ = 0;

6) при z₄ = 0, z₃ = 1, z₂ = 0, z₁ = 1;

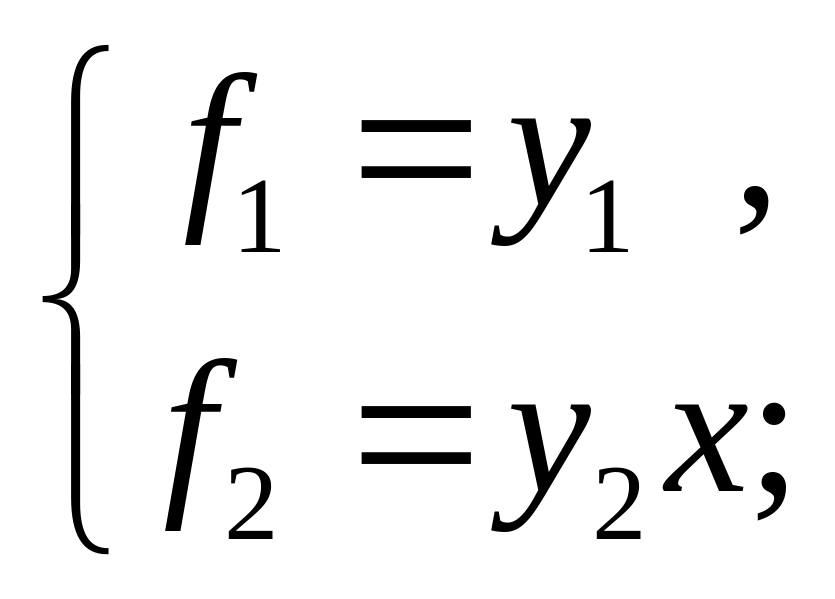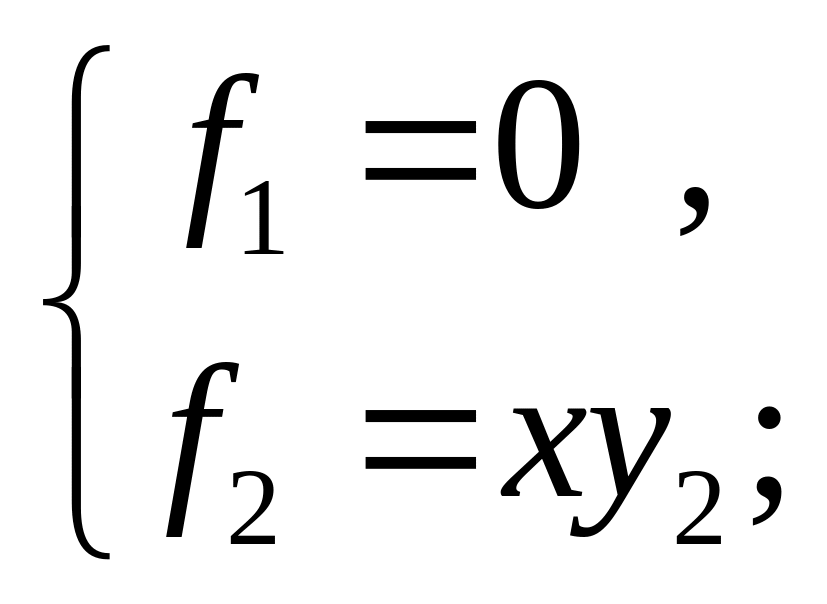5) (рис. 15, д) 6) (рис. 15, е)

7) при z₄ = 0, z₃ = 1, z₂ = 1, z₁ = 0;

8) при z₄ = 0, z₃ = 1, z₂ = 1, z₁ = 1;

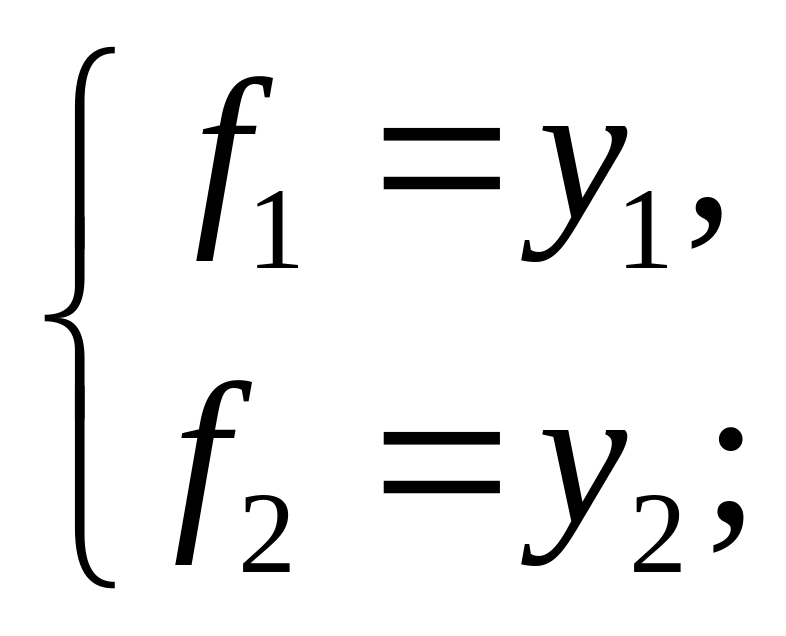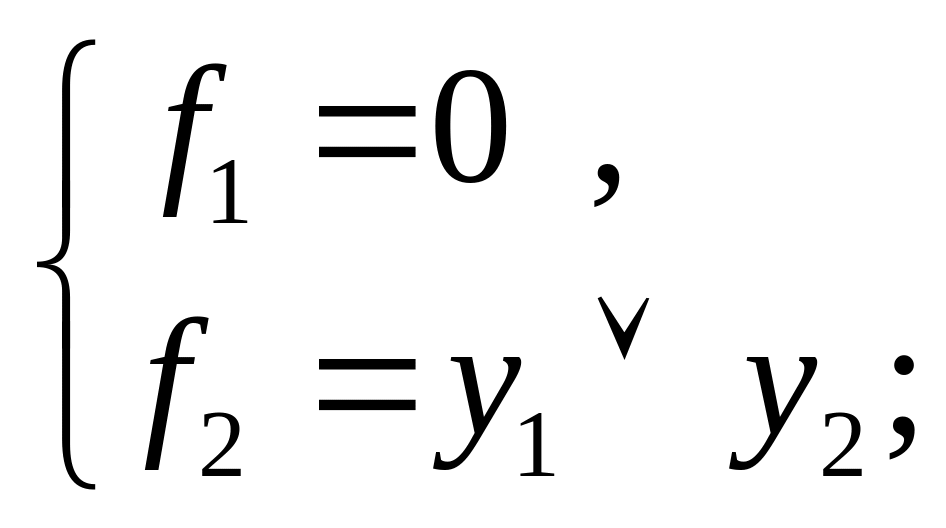7) (рис. 15, ж) 8) (рис. 15, з)

9) при z₄ = 1, z₃ = 0, z₂ = 0, z₁ = 0;

10) при z₄ = 1, z₃ = 0, z₂ = 0, z₁ = 1;

9) 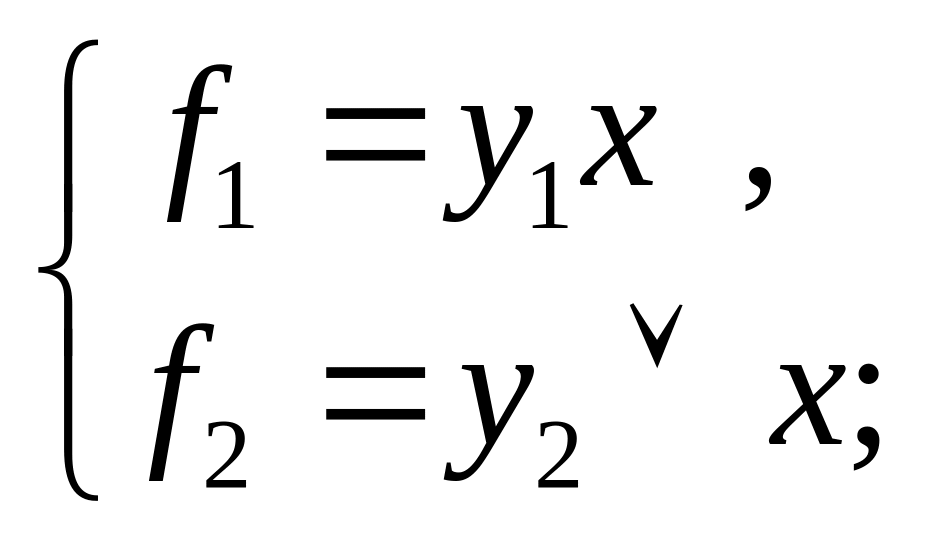(рис. 15, и) 10) (рис. 15, к)

11) при z₄ = 1, z₃ = 0, z₂ = 1, z₁ = 0;

12) при z₄ = 1, z₃ = 0, z₂ = 1, z₁ = 1;

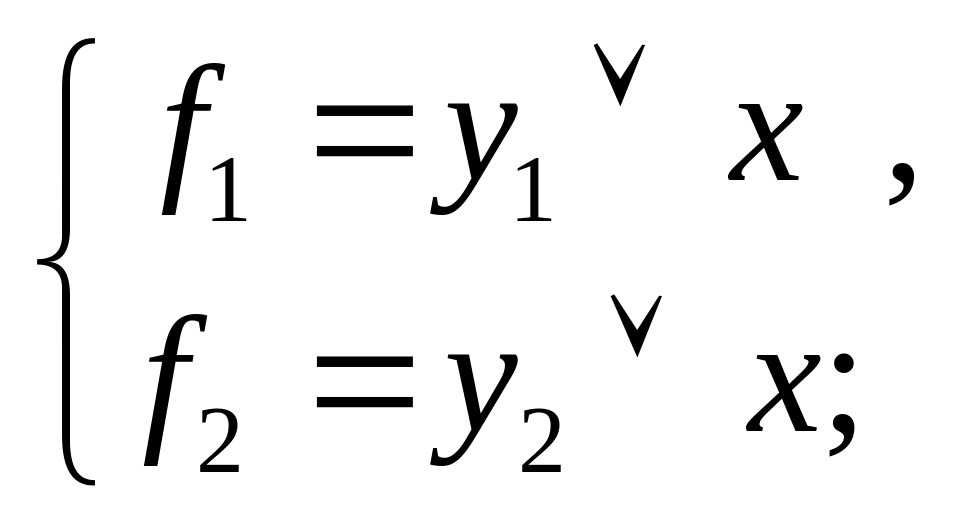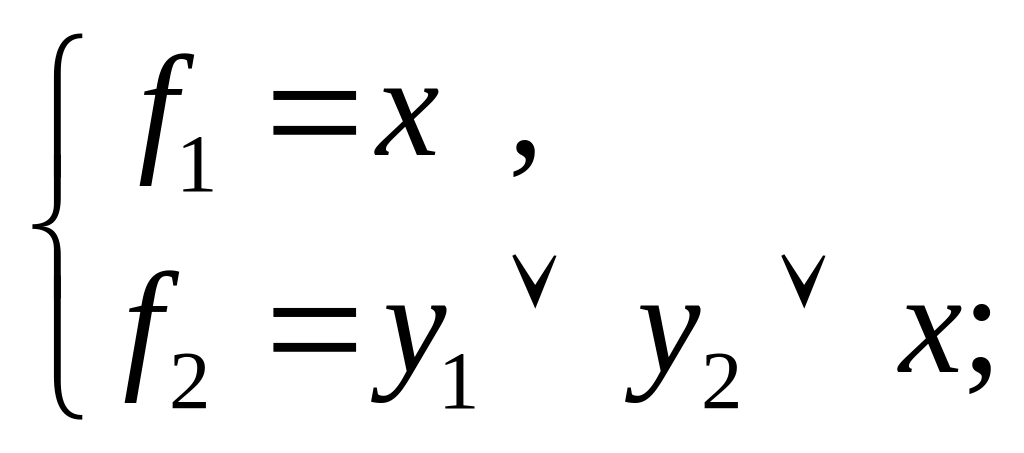11) (рис. 15, л) 12) (рис. 15, м)

13) при z₄ = 1, z₃ = 1, z₂ = 0, z₁ = 0;

14) при z₄ = 1, z₃ = 1, z₂ = 0, z₁ = 1;

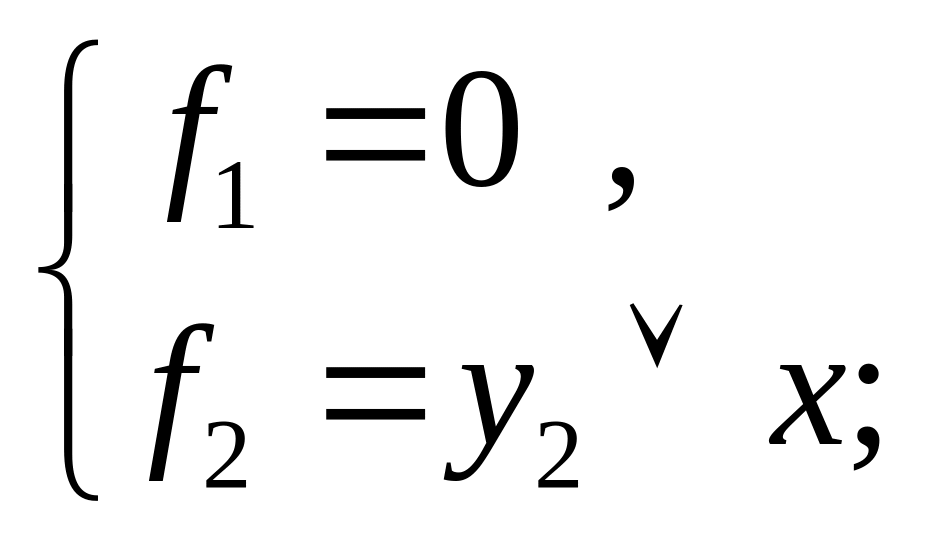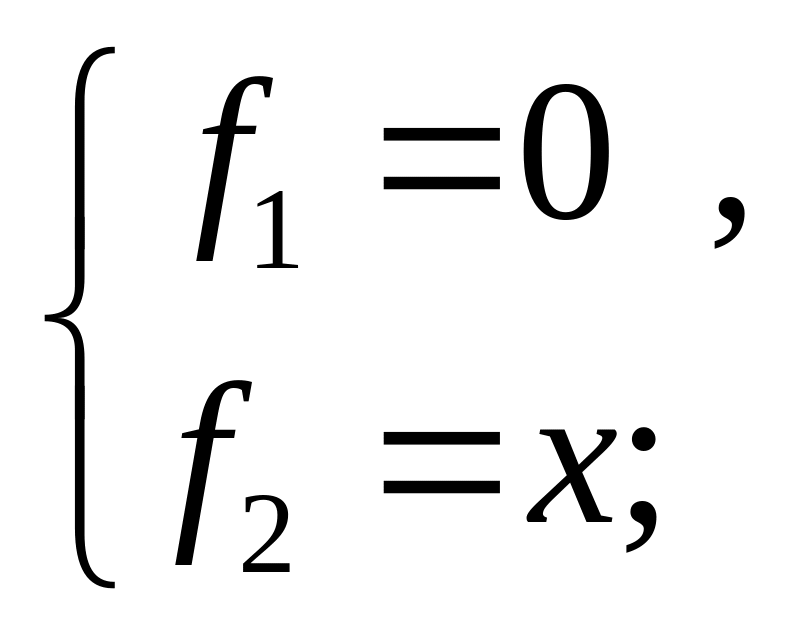13) (рис. 15, н) 14) (рис. 15, п)

15) при z₄ = 1, z₃ = 1, z₂ = 1, z₁ = 0;

16) при z₄ = 1, z₃ = 1, z₂ = 1, z₁ = 1;

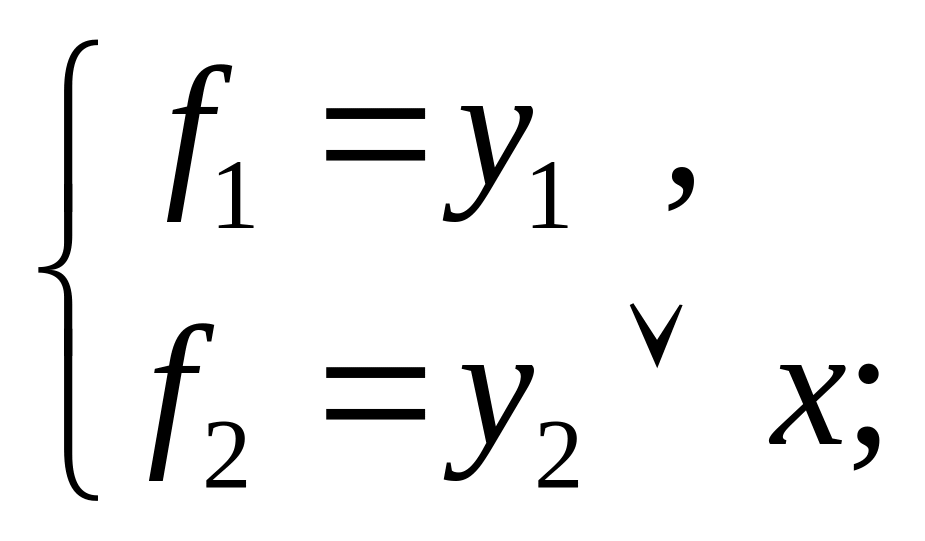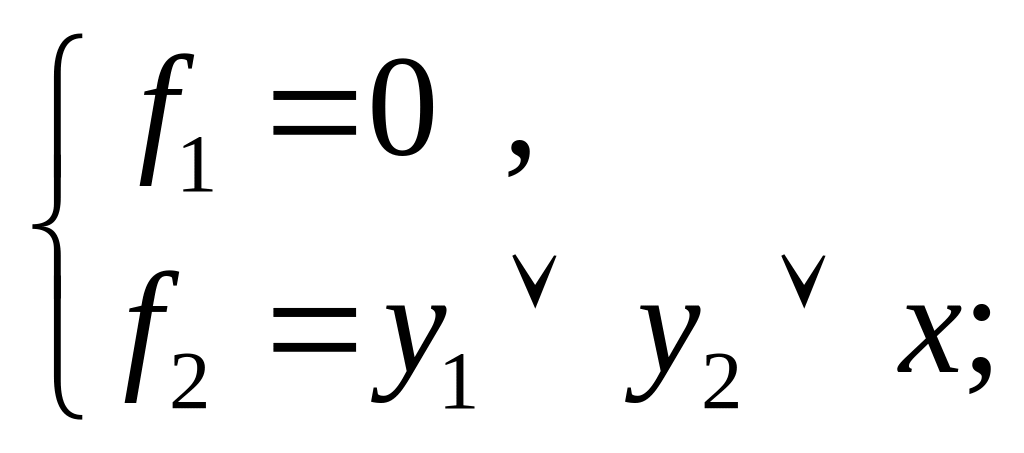15) (рис. 15, р) 16) (рис. 15, с)

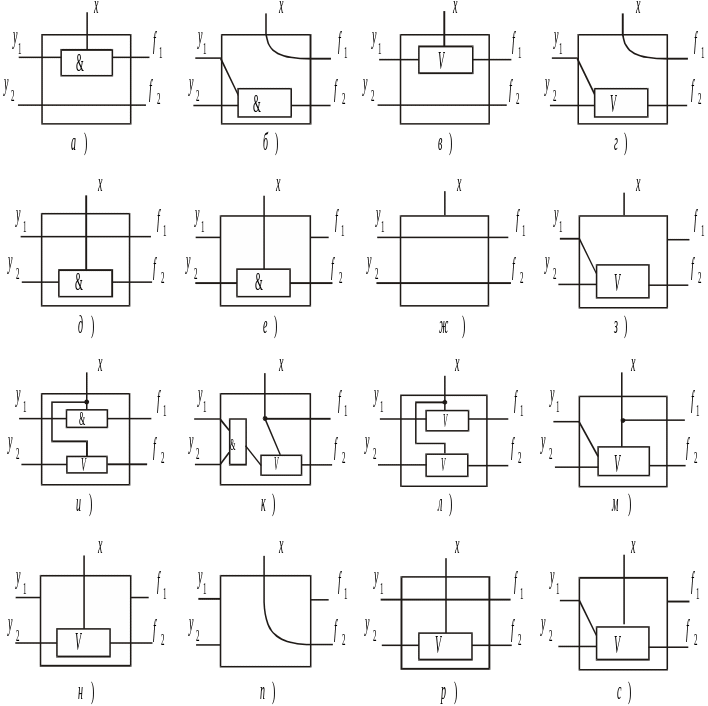
Рис. 15. Структурные схемы, полученные путем настройки

Проиллюстрируем работу изотропных сред (Н-структур), пост­роенных на Н-ячейках, на следующих примерах:

Пример 1. Реализация бесповторной неупорядоченной функции вида

f₁ = (x₁x₃ + x₄) x₂

представлена на рис. 16, где для каждой ячейки указаны настроечные коды, функция f₁ принадлежит подклассу J, поскольку l = x₁x₃ + x₄,  = x₂, q  0, а минимальный аргумент -функции входит в диапазон функции l. Нетрудно убедиться в том, что функция f₁ является неупорядоченной, так как среди всех фор­мул, получаемых путем тождественных преобразований, упорядоченные записи отсутствуют.

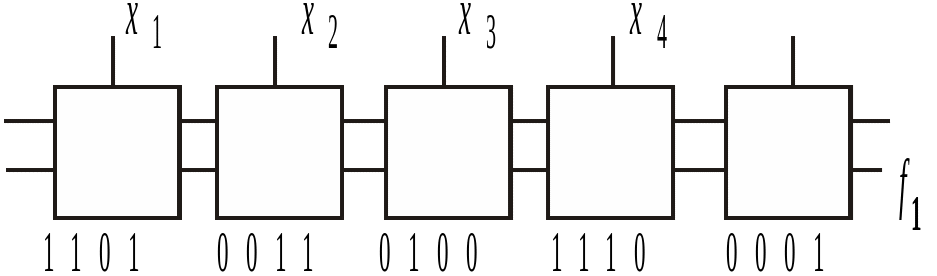
Рис. 16. К примеру 1

Пример 2. Аналогично для бесповторной неупорядоченной ни при каких тождественных преобразованиях функции

f₂ = x₁x₃ + x₂x₄ + x₆x₈ + x₉,

содержащей пропуски аргументов x₅ и x₇, имеем

l = x₁x₃,  = x₂x₄, q = x₆x₈ + x₉ .

Структура и настроечные коды ячеек приведены на рис. 17.

Рис. 17. К примеру 2

Пример 3. Рассмотрим случай реализации функции

f₃ = x₁x₂ + x₁x₃ + x₂x₃ +x₄ + x₅.

Функция f₃ является повторной, так как не существует никаких тождественных преобразований, в результате которых получалась бы за­пись с однократным вхождением в нее каждого аргумента. Настроечные коды для каждой ячейки изотропной среды, реализующей функцию f₃, представлены на рис. 18.

Рис. 18. К примеру 3

Пример 4. Реализация неупорядоченной функции высокого порядка

f₄ = {[(x₁x₆ + x₈)x₁₀ + x₁₁]x₁₂ + x₁₃} {[(x₂x₃x₄ +

+ x₅)x₇x₉ + x₁₄]} + [(x₁₅x₁₆ + x₁₇)x₁₈ + x₂₀] x₂₁

с пропуском аргумента x₁₉, настроечными кодами для каждой ячейки представлена на рис. 19.

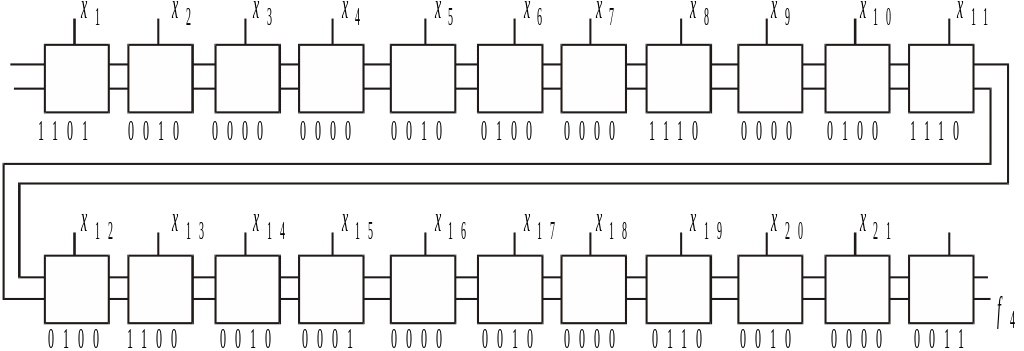
Рис. 19. К примеру 4

Таким образом, изотропные среды, построенные на Н-ячейках, обеспечивают реализацию как класса бесповторных упорядоченных произвольных нормальных формул из h букв (в том числе любых ско­бочных), так и формул из класса неупорядоченных и повторных фор­мул, определяемых подклассом J, и с успехом могут применяться в реализации сложных систем управления и обработки информации, обеспечивающих обработку больших массивов информации, формирование моделей сложных систем в реальном масштабе времени путем распараллеливания и одновременного выполнения сложных операций (быстрого преобразования Фурье, цифровой фильтрации сигналов, вычисления корреляционной функции, векторно-матричных преобразований и д.р.) [6].

Исследования, проводимые по данному направлению, нашли свое отражение в работах автора [108 – 110, 114, 116, 124, 125], и по результатам исследований в данной области получен акт внедрения (П. 2), а также подана заявка по выдаче патента Российской Федерации на изобретение (П. 3).