6. Определение кпд механизма.

Коэффициент полезного действия является показателем степени совершенства механизма.

Мгновенное значение КПД механизма:

где Вт – мощность, затрачиваемая на преодоление производственного (полезного) сопротивленя.

- суммарная мощность, затрачиваемая на преодоление трения во всех КП (“Вредные ” сопротивления).

Моменты трения во вращательных и силы трения в поступательных К.П.:

=260*0,1*0,15*0,09=0,234 Нм

=4440*0,1*0,1*0,32=14,208 Нм

=1590*0,1*0,1*0,3=4,77 Нм

=1590*0,1*0,1*0,3=4,77 Нм

=3435*0,1*0,1*0,045=1,54 Нм

=3382*0,01*0,1*0,045=1,52 Нм

3382*0,1=338,2 Нм

Радиусы цапф (r)определены по методике, изложенной в [3. Стр.12]

Тогда мощность трения в КП будет:

=0,234*20,93=4,897 Вт

=14,208*(20,93-5,2)=22,6 Вт

=4,77*6,2=29,574 Вт

=4,77*(-1,2)= -5,724 Вт

=1,5457*9,2=14,22 Вт

лист

=1,52*(5-9,2)=6,38 Вт

17

=338,2*4,2=1420,44 Вт

=

=4,897+226+29,57-5,72-6,38+14,22+1420,44=1683 Вт

тогда %=0,6%

Пояснительная записка составлена в соответствии с методикой, изложенной в [1. Стр.7-12]

лист

18

Для механизма АА найти числа зубьев колёс при следующих данных:

P=4

Примем:

Зубчатые колёса прямозубые, некоррелированные.

1.1 Определим передаточное отношение обращённого механизма по формуле (24)

1.2 Запишем в таблицу 1 все возможные варианты разложения на самножители.

№ вариантов разложения	1	2	3	4	5	6	7

Определим P, Q, P+Q по формуле 23

где , а значение С_1-3 берутся из таблицы 1 для соответствующего варианта.

Например для варианта 1 (С₁=1, С₂=1, С₂=24, С₃=25)

т.е. Р=49, Q=2, P+Q=51

Аналогично определяем P и Q для других вариантов, а результаты заносим в таблицу 2.

Таблица 2.

	1	2	3	4	5	6	7
Р	49	17	22	16	11	7	14
Q	2	7	9	13	18	17	17
P+Q	51	24	31	29	29	24	31

Из таблицы видно, что P+Q минимальную сумму имеет вариант 2.

1.4 Определим числа зубьев зубчатых колёс для варианта 2 по формуле30.

;

лит

;

П

20

одставив значения (С₁=2, С₂=5, С₂=12, С₃=5, Р=17, Q=7) получим:

;

;

Примем , получим: , , , .

1.5 Для сравнения проводим аналогичные расчёты для вариантов: 4, 5, 7. Результат заносим в таблицу 3.

Таблица 3.

№ варианта разложения	сомножители				Z1	Z2	Z2	Z3	Условие сборки	Габариты (мм)
	С1	С2	С2	С3						Г1	Г2
2	2	5	12	5	34	85	84	35	Не вып	595	595
4	8	5	6	10	64	40	39	65	Вып	520	520
5	8	10	6	5	88	110	108	90	Не вып	990	990
7	12	5	4	10	168	70	68	170	Не вып	1190	1190

По таблице 3 видно, что наименьшие габариты выдаёт вариант: 4

, , , .

6. Проверим выполнение передаточного отношения:

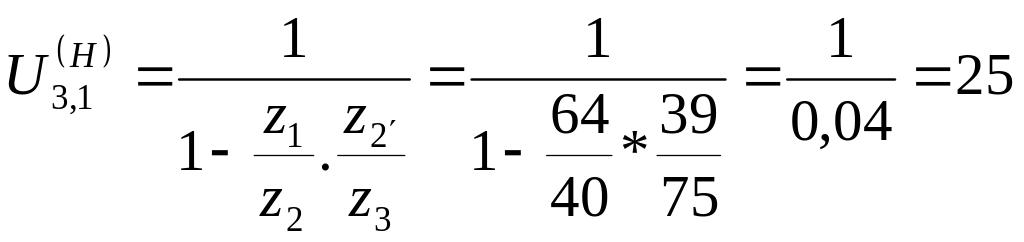
6. Проверим условие сносности:

5*(64+40)=5*(39+65)

520=520

6. Проверим условие сборки по формуле:

где К_2.2=4, D_2.2=1

6. Условие соседства:

0,707>0,4034

Условие сборки удовлетворяется.

Таблица 4.

Исходные данные
Параметры				Обозначение	Величина
Число зубьев		шестерни		Z4	14
		колеса		Z5	35
Модуль зацепления, мм				M	6
Исходный контур по ГОСТ 13755 - 68	Угол профиля, град				20
	Коэффициент высоты головки				1
	Коэффициент радиального зазора			С*	0,25
	Коэффициент радиуса кривизны переходной кривой				0,38
Коэффициент смещения			А	X4	0.68
				X5	0.522
			Б	X1	0
				X2	0

2. Расчёт удельного скольжения выполняется по формуле:

2.1 Расчёт удельного давления выполняется по формуле:

Значения величин удельного скольжения и удельного давления для зацеплений А и В приведены в таблицах 5 и 6.

Значения величин удельного скольжения и удельного давления для неравно смещенного зацепления А

Таблица 5

	N4		P2	П		P1				N5
х	0	25	51.54	76.77	100	133.63	170	200	230	271.43
е-х	271.43	246.43	219.89	194.46	171.43	137.8	101.43	71.43	41.43	0
		-2.942	-0.711	0	0.314	0.587	0.761	0.857	0.927	1
	1	0.746	0.414	0	-0.458	-1.424	-3.19	-5.999	-12.87
		0.22	0.119	0.09	0.0791	0.0737	0.0787	0.0949	0.1424

Значения величин удельного скольжения и удельного давления для равно смещенного зацепления В.

Таблица6.

	N4		П			P1				N5
х	0	25	59.73	80	100	111.85	140	170	190	203.4
е-х	203.4	178.4	143.67	123.4	103.4	91.55	63.4	33.4	13.4	0
		-1.854	0	0.383	0.586	0.672	0.818	0.921	0.971	1
	1	0.649	0	-0.620	-1.41	-2.054	-4.52	-11.72	-34.44
		0,228	0,1185	0,103	0,098	0,099	0,1145	0,179	0,399

3 Коэффициент полезного действия.

Коэффициент полезного действия (КПД) является важным показателем качества планетарного механизма. Он может быть вычислен приближённо по формулам, приведённым в таблице 3 стр.12 методическое пособие «Кинематический синтез типовых планетарных механизмов»

3.1 Значение КПД планетарного механизма:

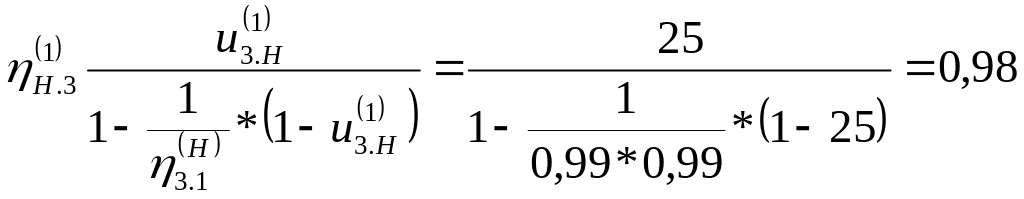
для пары зубчатых колёс можно принять:

3.2 Значение КПД механизма:

4 Частота вращения