
Semestr1-hyper1
.pdf
Последовательность {xk} – ограниченная, поэтому из неё можно выделить сходящуюся подпоследовательность {xkj } : xkj → c, c [a, b]. Заметим, что ykj → c, так как ykj =
1 (ykj − xkj ) + xkj и 0 < |ykj − xkj | < kj
c [a, b], поэтому f(xkj ) − f(ykj ) → f(c) − f(c) = 0, что противоречит (4.4).
Замечание 4.3. Из равномерной непрерывности f(x) на E следует непрерывность f(x) на E. Обратное утверждение, вообще говоря, не верно. Например: f(x) = 1/x, x (0, 1) – непрерывна, но не равномерно непрерывна на
(0, 1). Действительно, если для любого δ > 0 выбрать x = δ > 0 и y = δ/2, то |x − y| < δ, но |f(x) − f(y)| = |x1 − y1 | = 1δ > 1 (считаем, что δ (0, 1)).
Пусть функция f : E → R определена на некотором множестве E R и F E – другое, более широкое, множество в R. Любая функция f˜: F → R, определенная на F и совпадающая с f на E, называется продолжением f с E на F .
Теорема 4.5. Пусть f : E → R равномерно непрерывна на E и E0 – множество всех предельных точек множества E. Тогда f допускает равномерно непрерывное продолжение на множество F = E S E0.
0 ˇ
Доказательство. Пусть a E . Так как a – предельная точка множества E, то любая U(a) содержит бесконечное множество точек из E. Функция f равномерно непрерывна на E, поэтому
ˇ 0 00 ˇ ∩ | 0 − 00 |
ε > 0 U(a) : x , x U(a) E ( f(x ) f(x ) < ε.
Это значит, что для функции f выполняется условие Коши существования предела функции
lim f(x). Определим
x→a
f˜(a) = |
(lim f(x), |
если a |
E0 |
|
E. |
||
|
f(a), |
если a |
E, |
|
|
||
|
x |
→ |
a |
|
|
\ |
|
|
|
|
|
|
|
|
|
Убедимся, что f˜: F → R равномерно непрерывна на F . Пусть ε > 0 – произвольно и δ > 0 такое, что
x0, x00 E : |x0 − x00| < 3δ |f(x0) − f(x00)| < ε/3. |
(4.5) |
Пусть z, y F и |y − z| < δ. Тогда существуют числа δ0, δ00 (0, δ) такие, что |
|
|x0 − y| < δ0 |f(x0) − f˜(y)| < ε/3, |
(4.6) |
|x00 − z| < δ00 |f(x00) − f˜(z)| < ε/3. |
(4.7) |
Действительно, если y, z E F , то (4.6) и (4.7) следуют из (4.5), так как δ0 |
и δ00 < 3δ. |
Если же y, z F \E, то (4.6) и (4.7) следуют из того, что f˜(y) = lim f(x), f˜(z) = lim f(x).
|
|
|
|
|
|
|
|
|
|
|
Uδ0(y) |
E, x00 Uδ00(z) |
x→y |
|
x→z |
|
||||||
Выберем теперь x0 |
E (здесь Uδ0(y) = (y − δ0, y + δ0), Uδ00(z) = |
|||||||||||||||||||||
(z |
− |
δ00, z + δ00) |
) и запишем |
T |
|
|
T |
|
|
|
|
|||||||||||
|
|
|
|
|
|
очевидное неравенство |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|f˜(y) − f˜(z)| = |f˜(y) − f(x0) + f(x0) − f(x00) + f(x00) − f˜(z)| ≤ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
≤ |f˜(y) − f(x0)| + |f(x0) − f(x00)| + |f(x00) − f˜(z)|. |
|
|
(4.8) |
|||||||
Учитывая, что x0 Uδ0(y) |
E, x00 |
Uδ00(z) |
E и что |x0 − x00| = |x0 − y + y − z + z − x00| ≤ |
|||||||||||||||||||
| |
x0 |
− |
| |
| |
|
− |
|
| |
| |
|
− |
x00 |
| T |
|
, используя (T |
|
|
ε > 0 |
|
|
||
|
|
|
y |
+ |
y |
|
z |
+ |
z |
|
< 3δ |
|
4.5) - (4.7), мы получили из (3.1): |
|
|
δ > |
||||||
0 y, z F (|y − z| < δ |f˜(y) − f˜(z)| < ε). Равномерная непрерывность функции f˜ на F доказана. 
4.5Непрерывность обратной функции
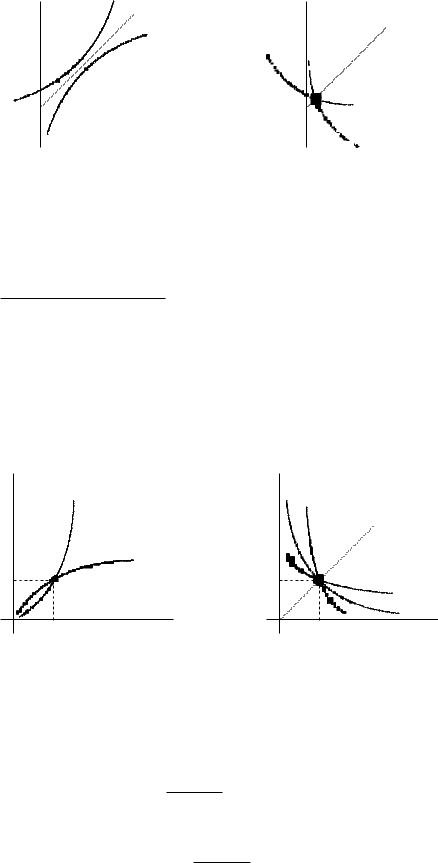
Пусть кривая является графиком функции y = f(x)(x E, y F ). Если кривая определяет x как функцию y, т. е. каждому y ставится в соответствие с помощью (см. рис. 1) единственная точка x, то говорят, что определена x = g(y)(y F ) – функция, обратная к функции f.
31
6
'
y 







 (x, y)
(x, y)
0 x - x
Рис. 1.
Замечание 4.4. Графиком обратной функции x = g(y) (y F ) является кривая 0, являющаяся зеркальным отображением кривой относительно биссектрисы I и III координатных углов. Действительно, если = {(x, f(x)) R2|x E} – график функции f(x), то графиком обратной функции будет кривая 0 = {(y, g(y)) R2|y F } = {(y, x) R2|y F }. Отсюда следует справедливость замечания.
Лемма 4.3. Если y = g(x) (x F ) – функция, обратная к функции y = f(x) (x E), то справедливы два тождества: x ≡ g(f(x)) (x E) и y ≡ f(g(y)) (y F ).
Доказательство. Пусть x E (x, f(x)) (f(x), x) 0 x = g(f(x)). Так как x
произвольно, то доказана справедливость первого тождества. Второе тождество доказывается аналогично. 
Теорема 4.6. (Критерий существования обратной функции) Пусть функция f : E → R строго возрастает (x1 < x2 f(x1) < f(x2)) или строго убывает (x1 < x2 f(x1) > f(x2)) и F = f(E). Тогда существует обратная к f функция g : F → R, которая строго возрастает (соответственно, строго убывает).
Доказательство. Пусть функция f : E → R строго возрастает. Покажем, что тогда существует функция, обратная к функции f, и что она будет так же строго возрастать. Для этого нужно показать, что кривая , являющаяся графиком функции f, определяет x как функцию y(y F ). Это будет выполняться, если любая прямая, параллельная оси Ox, пересекает кривую только в одной точке. Допустим, что этого нет и какая-то прямая, параллельная оси Ox, пересекает кривую в точках x1 < x2. Следовательно, одному значению y = f(x1) = f(x2) соответствуют два значения x1 < x2, а это противоречит строгому возрастанию функции f. Таким образом, любая прямая, параллельная оси Ox, пересекает только в одной точке. Это означает, что определена обратная к f функция x = g(y) (y F ). Обратная функция x = g(y) (y F ) – строго возрастающая, так как из y1 = f(x1) < y2 = f(x2) следует x1 < x2 (в противном случае мы получим противоречие строгому возрастанию функции f). 
Теорема 4.7. Пусть y = f(x) непрерывна и строго возрастает на [a, b]. Тогда образ f([a, b]) = [A, B], A = f(a), B = f(b) и на [A, B] определена обратная к f функция x = g(y), строго возрастающая и непрерывная.
Доказательство. Прежде всего докажем, что f([a, b]) = [A, B]. Так как f строго монотонна, то очевидно f([a, b]) [A, B] и f(a) < f(b). Далее, из непрерывности f в силу теоремы Больцано-Коши о промежуточных значениях следует, что для любого y [A, B] существует x [a, b] : f(x) = y. Таким образом, [A, B] f([a, b]) и в итоге f([a, b]) = [A, B]. Теперь из теоремы 4.6 следует существование обратной строго возрастающей функции g на отрезке
[A, B].
Остается доказать непрерывность g на [A, B]. Пусть y0 [A, B] и yn [A, B] такие, что yn → y0. Положим x0 = g(y0), xn = g(yn). Тогда, из свойства обратной функции, следует y0 = f(g(y0)), yn = f(g(yn)) = f(xn). Непрерывность функции g в точке y0 будет доказана, если мы покажем, что xn → x0. Допустим, что это не так. Тогда существует подпоследовательность xnk → x0, причем x0 [a, b] и x0 6= x0 (существование такой подпоследовательности следует из теоремы Больцано-Вейерштрасса). Так как x0 6= x0, то в силу строгого возрастания функции f: f(x0) 6= f(x0). Последовательность {f(xnk )} является под-
последовательностью {yn}, сходящейся к y0, поэтому f(xnk ) = ynk → y0 = f(x0) 6= f(x0). Получено противоречие, доказывающее, что xn → x0. 
32

Теорема 4.8. Пусть f(x) непрерывна и строго возрастает на (a, b) и пусть
A = inf |
f(x), B = sup f(x), |
x (a,b) |
x (a,b) |
причем допускаются значения a = −∞, A = −∞, b = +∞ и B = +∞. Тогда образ (a, b) есть (A, B), и обратная к f(x) функция x = g(y) строго возрастает и непрерывна на (A, B).
Доказательство. Установим сначала, что f((a, b)) (A, B). Если B < +∞, то по определению супремума f(x) ≤ B для всех x (a, b), а в случае B = +∞ это неравенство очевидно. Докажем, что B / (a, b). Допустим противное, т.е. что существует точка x1 (a, b) такая, что f(x1) = B. Тогда найдется точка x2 : x1 < x2 < b, в которой в силу строгого возрастания функции f значение f(x2) > f(x1) = B, что противоречит определению B. Аналогичные рассуждения можно провести и для A. Итак, доказано включение f((a, b)) (A, B).
Докажем теперь обратное включение. Пусть y (A, B), тогда, в силу определения A и B, существуют x1, x2 (a, b) такие, что y1 = f(x1) < y < f(x2) = y2. А так как f(x) строго возрастает, то должно быть x1 < x2. Функция f(x) непрерывна на [x1, x2] (a, b), поэтому существует единственная точка x [x1, x2] такая, что f(x) = y для любой y (A, B). Это означает, что (A, B) f((a, b)). В итоге f((a, b)) = (A, B).
Из теоремы 4.6 следует существование обратной строго возрастающей функции g на (A, B). Проверим, что g(y) непрерывна в любой точке интервала (A, B). Пусть y (A, B). Очевидно функцию g(y), считая её определенной при y [f(x1), f(x2)] можно рассматривать как функцию, обратную к функции f(x), определенной на [x1, x2] (существование точек x1 и x2 мы доказывали выше для любой точки y (A, B)). Так как f(x) непрерывна на [x1, x2], то по теореме 4.7 g(y) будет непрерывна на [f(x1), f(x2)], т. е. в точке y [f(x1), f(x2)] (A, B). Точка y – произвольная точка из (A, B), поэтому g(y) – непрерывна на (A, B). 
Замечание 4.5. В теоремах 4.7 и 4.8 можно заменить "возрастающая" на "убывающая", и тогда в их заключениях надо заменить, соответственно,
[A, B] на [B, A] и (A, B) на (B, A).
Замечание 4.6. В теореме 4.8 интервалы (a, b), (A, B) можно, соответственно, заменить на полуинтервалы, например, на [a, b), [A, B), и тогда a и A – конечные числа.
4.6 Элементарные функции
Показательная функция
Пусть n N, a R, a > 0. Число an = a · · · a (по определению). Число a1/n
| {z
{z }
}
n раз
– арифметический корень n-й степени из числа a. Если n/m – неотрицательное рациональное число, то (по определению) полагаем an/m = (a1/m)n = (an)1/m. Таким образом, мы определили функцию f(p) = ap, p Q. Из элементарной алгебры известно, что ap (p Q) обладает свойствами:
1.ap+q = ap · aq.
2.ap строго возрастает при a > 1 и строго убывает при a < 1.
Возникает вопрос, можно ли доопределить функцию f(p) = ap (p Q) на иррациональных числах так, что, определенная уже на всей числовой прямой R, продолженная функция будет непрерывной на R и удовлетворять свойствам 1. и 2. Докажем существование такой функции. Начнем с того, что докажем равномерную непрерывность f(p) = ap на любом отрезке [−N, N] T Q, n N.
T
Пусть для определенности a > 1. Если p < q (p, q [−N, N] Q), то 0 < aq − ap = ap(aq−p − 1) < aN (aq−p − 1). Пусть ε > 0 - произвольное число и n0 N такое, что если n > n0, то
|a1/n − 1| < ε · a−N |
(1) |
(этого можно добиться, так как lim a1/n = 1).
33

Таким образом, если 0 < q − p ≤ |
|
1 |
, то мы получим, используя (1), что |
||||||||||||||||||||||||||
n0+1 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 < aq − ap < aN (a |
|
− 1) < ε. |
|
|
|
|
|
|
|
|
|
|
(2) |
|||||||||||||
|
|
n0+1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Далее, если p > q, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
0 < ap − aq = aq(ap−q − 1) < aN (ap−q − 1). |
|
|
|
|
|
|
|||||||||||||||||||||
Отсюда, используя (1), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
0 < ap − aq < aN (a |
n0+1 |
− 1) < ε, если 0 < p − q ≤ |
|
|
. |
|
|
(3) |
|||||||||||||||||||||
n0 + 1 |
|
|
|||||||||||||||||||||||||||
Перепишем (2) следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
если |
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ |
p |
− |
q < 0, |
то − |
ε < ap |
− |
aq |
< 0. |
|
|
|
|
|
|
|
(4) |
|||||||||
|
|
|
n0 + 1 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
p |
|
q |
|
||
Из (4) и (3) p, q [−N, N] Q справедливо: |p−q| ≤ |
|
|a |
−a |
| < ε, |
|||||||||||||||||||||||||
n0+1 |
|||||||||||||||||||||||||||||
что означает равномерную непрерывность ap на любом отрезке [ |
− |
N, N] . |
|||||||||||||||||||||||||||
Любая точка |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
R |
|
T |
определить функцию f(x) следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
ax, |
|
если x |
Q, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
f(x) = (lim ap, |
|
если x R |
Q. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
p→x |
|
|
|
|
|
|
\ |
|
|
|
|
|
|
|
|
|
|
|
|
||
Докажем, что это и есть искомая нами функция. Пусть x R\Q. Накроем эту точку некоторым отрезком [−N, N], N N. Выше была доказана равномерная непрерывность функции ap, p Q на множестве [−N, N] T Q. Так как функция f(x) является продолжением функции ap, p [−N, N] T Q, то по теореме "Продолжение по непрерывности" (см. § 4.4), f(x) будет равномерно непрерывна на [−N, N], а следовательно, просто непрерывна в точке x R\Q. Любая точка x R\Q может быть накрыта отрезком [−N, N], поэтому f(x) будет непрерывна в любой точке x R.
Вновь определенную функцию обычно обозначают f(x) = ax, x R и называют показательной функцией. Докажем справедливость свойств 1. и 2. для показательной функции ax, x R. Пусть x, y R\Q, причем x < y. Существуют рациональные числа p, q такие, что x < p < q < y (см. § 1.3 "Свойства порядка действительных чисел" ). Пусть pn, qn Q такие, что pn → x (возрастая), а qn → y (убывая) apn < ap < aq < aqn . Переходя к пределу, получим ax ≤ ap < aq ≤ ay. Таким образом, мы доказали свойство 2. Свойство 1. следует из равенства apn+qn = apn · aqn после перехода к пределу.
Если a < 1, то полагаем ax = (1/a1 )x . Функция (1/a)x, по доказанному выше, будет непрерывна на R, (1/a)x > 0 при x R, поэтому функция ax (a < 1) будет непрерывна на R. Заметим, что при a < 1 функция ax будет строго убывать.
При a = 1 полагаем: 1x = 1 при любом x R.
Логарифмическая функция
Определение 4.9. Функция, обратная к показательной y = ax (x R), a > 0, a 6= 1, называется логарифмической и обозначается y = loga x, x > 0.
34
y 6 |
|
|
|
|
|
y 6 |
||||||||||||||||||||
|
|
|
|
y=ax |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y= loga x |
|
y=a |
x |
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y= loga x |
x |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Рис. 1. (a > 1) |
|
|
Рис. 2. (a < 1) |
|
||||||||||||||||||||
Логарифмическая функция будет непрерывной как функция, обратная к показательной (непрерывной) функции.
Из свойства обратной функции следует:
1.aloga x = x (x > 0).
2.loga(ax) = x (x R.
Степенная функция
y = xb (b – постоянная, x – переменная, x > 0) – степенная функция. Согласно свойствам логарифмической функции xb = eb ln x(x > 0), ln x – непре-
рывная функция, показательная функция - непрерывна, суперпозиция двух непрерывных функций есть функция непрерывная, поэтому степенная функция будет непрерывной.
Из |
xb |
= |
eb ln x |
x > |
lim |
xb = 0, |
lim |
xb = + , |
(b > 0) |
, а также |
|
|
( |
|
0) x 0+0 |
x |
+ |
∞ |
∞ |
|
|||
|
|
|
|
|
→ |
|
→ |
|
|
|
|
тождество: (xy)b = xb · yb (b – произвольно). |
|
|
|
|
|
||||||
y |
|
|
|
|
|
y |
|
|
|
|
|
6 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
β=2 |
|
|
|
|
|
|
|
|
|
|
|
β=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β=1/2 |
|
1 |
|
1 |
|
|
|
β=1/2 |
|
|
|
|
|
β=1 |
|
|
- |
|
β=2 |
|
|
|
|
|
- |
|
0 |
1 |
x |
0 |
1 |
x |
|
Рис. 1. (β > 0) |
|
|
Рис. 2. (β < 0) |
|
Гиперболические функции |
|
|
|
|||||||||||
|
sinh x = |
ex − e−x |
– гиперболический синус, |
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
cosh x = |
ex + e−x |
|
– гиперболический косинус, |
||||||||||
|
|
|
|
|||||||||||
|
|
sinh x |
2 |
ex − e−x |
|
|||||||||
tanh x = |
= |
– гиперболический тангенс, |
||||||||||||
|
|
|
|
|||||||||||
|
cosh x |
|
ex + e−x |
|||||||||||
|
cosh x |
|
ex + e−x |
|
|
|||||||||
coth x = |
|
= |
|
(x 6= 0) – гиперболический котангенс. |
||||||||||
sinh x |
ex − e−x |
|||||||||||||
Из непрерывности показательной функции и арифметических свойств непрерывных функций следует непрерывность гиперболических функций: sinh x (x
R), cosh x (x R), tanh x (x R), coth x (x R, x 6= 0).
35

y 6 |
|
y 6 |
|
ch x |
sh x |
|
|
|
|
|
|
|
|
|
coth x |
1 |
- |
1 |
tanh-x |
|
|
||
0 |
x |
0 |
x |
|
|
−1 |
|
|
|
coth x |
|
Замечание. Для гиперболических функций имеют место формулы, аналогичные формулам для тригонометрических функций. Например, cosh2 x − sinh2 x = 1, 2 cosh x sinh x = sh 2x, sinh(x ± y) = sinh x cosh y ± cosh x sinh y
и т. д.
Упражнения
1.Что можно сказать о непрерывности в точке x0 функций f(x) + g(x), f(x)g(x), если
a)функция f(x) непрерывна в точке x0, а функция g(x) разрывна в точке x0?
b)обе функции разрывны в точке x0?
2.Пусть нечетная функция f непрерывна в нуле. Доказать, что f(0) = 0. Какие значения может принимать f(0), если снять условие непрерывности?
3.Существует ли функция, непрерывная на отрезке и отображающая его на [0, +∞) ?
4. |
Существует ли функция, непрерывная на отрезке и отображающая его на [0, 1] [3, 4] |
|
|
? |
|
5. |
Пусть функция f(x) > 0 и непрерывна на отрезке [a, b]. Доказать, что существует |
|
|
m > 0 : |
x [a, b] |
|
f(x) ≥ m |
|
6. |
Пусть функция f(x) удовлетворяет условию Гельдера на интервале (a, b): |
|
|
|f(x) − f(y)| ≤ k|x − y|α x, y (a, b) |
|
где k, α - положительные постоянные. Доказать, что f(x) равномерно непрерывна на
(a, b).
7.Пусть функция f монотонна на [a, b], f(a) и f(b) – конечные числа и f принимает все промежуточные значения между f(a) и f(b). Доказать, что f непрерывна.
8.Пусть f непрерывна в точке a и для каждого δ > 0 существуют точки xδ, yδ Uδ(a) (из δ-окрестности точки a) такие, что f(xδ) f(yδ) < 0. Доказать, что f(a) = 0.
9. Пусть f непрерывна на [a, b) и имеет конечный левый предел в точке b. Доказать, что
f ограничена на [a, b].
10.Пусть функция f непрерывна на [a, b]. Доказать, что функции
|
|
|
m(x) = inf f(x), |
M(x) = sup f(x) |
|
|
|
|
|
a≤x |
a≤x |
|
|
также непрерывны на [a, b]. |
|
|
|
|||
11. Пусть функция f непрерывна на [a, b]. Доказать, что функции |
|
|||||
| |
f(x) |
, f+(x) = max(f(x), 0), f−(x) = max( |
− |
f(x), 0) |
||
|
| |
|
|
|
||
также непрерывны на [a, b]. |
|
|
|
|||
12. Пусть функции f, |
g непрерывны на [a, b]. Доказать, что функции |
|||||
|
|
|
max(f(x), g(x)), |
min(f(x), g(x)) |
|
|
также непрерывны на [a, b]. |
|
|
|
|||
36
13.Доказать, что если функция непрерывна на некотором отрезке и не имеет локальных экстремумов, то она монотонная.
14.Доказать, что если функция непрерывна и обратима на некотором отрезке, то она строго монотонна на этом отрезке.
37

§5 Дифференциальное исчисление функций одной переменной
5.1Производная и дифференциал первого порядка
Пусть функция f(x) определена в некоторой окрестности U(x0) точки x0 R и x0 + x U(x0) при | x| < δ. Тогда в проколотой δ-окрестности нуля (−δ, 0) (0, δ) определена функция
ψ(Δx) = f(x0 + x) − f(x0). x
Определение 5.1. Если существует предел
lim ψ(Δx) = |
lim |
f(x0 + |
x) − f(x0) |
, |
|
||||
|
x |
|||
x→0 |
x→0 |
|
||
то он называется производной от функции f в точке x0 и обозначается f0(x0). Производная может быть конечной, +∞ или −∞.
Определение 5.2. Если существует односторонний предел
f+0 (x0) = lim |
f(x0 + |
x) − f(x0) |
, |
|
|||
|
x |
||
x→+0 |
|
||
то он называется правой производной от функции f в точке x0. Аналогично, если существует односторонний предел
f0 |
(x0) = |
lim |
f(x0 + |
x) − f(x0) |
, |
|
|||||
|
x |
||||
− |
|
x→−0 |
|
||
то он называется левой производной от функции f в точке x0. Односторонние производные f+0 (x0) и f−0 (x0) могут быть конечными или
±∞.
Лемма 5.1. Если функция f имеет конечную производную f0(x0) в точке x0, то она непрерывна в этой точке.
Доказательство. Из существования конечного предела lim ψ(Δx) следует ограниченность
x→0
ψ(Δx) при малых | x| ≤ δ, т.е.
f(x0 + x) − f(x0)
≤ C = const при | x| ≤ δ
x
откуда
|f(x0 + x) − f(x0)| ≤ C| x| → 0 при x → 0.
Лемма 5.2. Для того, чтобы существовала производная f0(x0), необходимо и достаточно, чтобы существовали правая и левая производные от f в точке x0 и были равны между собой, при этом f0(x0) = f+0 (x0) = f−0 (x0).
Доказательство. Справедливость сформулированного утверждения следует из леммы 3.2:
предел lim |
f(x0 + |
x) − f(x0) |
= f0 |
(x0) существует тогда и только тогда, когда существу- |
|||||||
|
|||||||||||
x→0 |
x |
|
|
|
|
|
|
|
|||
ют односторонние пределы lim |
f(x0 + |
x) − f(x0) |
и |
lim |
f(x0 + |
x) − f(x0) |
и они |
||||
|
|
||||||||||
|
x |
|
x |
||||||||
|
|
x→+0 |
|
|
x→+0 |
|
|||||
равны.
Примеры и иллюстрации
1. Если f непрерывна в точке x, то она может и не иметь производной в этой точке. Примером является функция f(x) = |x|, непрерывная во всех точках, но не имеющая
38

производной в точке 0. В этой точке существуют односторонние производные f+0 (0) = 1 и f−0 (0) = −1.
2. Функция, имеющая в точке бесконечную производную, может иметь в этой точке разрыв. Например, функция y = sgnx = {1 при x > 0; 0 при x = 0; −1 при x < 0} имеет бесконечные односторонние производные в точке 0:
y0 |
(0) = |
lim |
|
y(0 + h) − y(0) |
= y0 |
(0) = |
lim |
y(0 + h) − y(0) |
== + |
∞ |
. |
|||
− |
|
h |
→− |
0 |
h |
+ |
|
h |
→ |
+0 |
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда y0(0) = +∞, но при этом функция y = sgnx в точке x = 0 имеет разрыв 1-го рода.
|
|
1 |
|
|
|
|
|
|
|
|
x = 0 |
|
|
0, |
|||
3. Другим примером является функция f(x) = x, |
x 6= 0,, которая имеет в точке x = 0 |
||||
бесконечный разрыв. В то же время в этой |
точке существует бесконечная производная: |
||||
|
|
||||
y0(0) = +∞. |
|
|
|
|
|
4. Функция |
|
|
|
|
|
0 |
если x- рациональное число, |
||||
f(x) = (x2 |
если x- иррациональное число |
||||
имеет разрывы всюду, кроме точки x = 0, в которой она не только непрерывна, но и имеет производную f0(0) = 0.
Доказательство. Поскольку |
|
|
|
|
|
|
f(Δx) f(0) = |
0 |
если |
x − рациональное число, |
|||
− |
((Δx)2 если x |
− |
иррациональное число, |
|||
|
||||||
то существует производная |
|
|
|
|
|
|
|
f0(0) = |
lim |
f(Δx) − f(0) |
= 0. |
||
|
|
x→0 |
|
x |
||
В силу леммы 5.1 функция f(x) и непрерывна в точке x = 0
Сдругой стороны, функция f(x) разрывна во всех точках x 6= 0. Действительно, пусть x 6= 0 и x – рациональное число, так что f(x) = 0. Возьмем последовательность иррацио-
нальных чисел {xn}, сходящуюся к x. Тогда f(xn) = x2n → x2 6= f(x). Если же x 6= 0 и x
– иррациональное число, то f(x) = x2. Возьмем последовательность рациональных чисел
{xn}, сходящуюся к x. По определению f(xn) = 0 n, поэтому f(xn) → 0 6= f(x).
y 6 |
y 6 |
|
y 6 |
y 6 |
y 6 |
y 6 |
|
|
|
E |
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
- |
|
- |
- |
- |
- |
- |
0 x0 |
x 0 |
x0 |
x 0 x0 |
x 0 |
x0 x 0 |
x0 x 0 |
x0 x |
Рис. 1 |
Рис. 2 |
Рис. 3 |
|
Рис. 4 |
Рис. 5 |
Рис. 6 |
|
Рис. 1. Функция имеет конечную производную f0(x0) (график в этой точке имеет касательную, причем единственную).
Рис. 2. Функция не имеет производной, но существуют конечные левая f−0 (x0) и правая f+0 (x0) производные, не равные друг другу.
Рис. 3. Функция имеет бесконечную производную f0(x0) = +∞. Рис. 4. Функция имеет бесконечную производную f0(x0) = −∞. Рис. 5. Функция не имеет производной, f−0 (x0) = +∞, f+0 (x0) = −∞. Рис. 6. Функция не имеет производной, f−0 (x0) = −∞, f+0 (x0) = +∞.
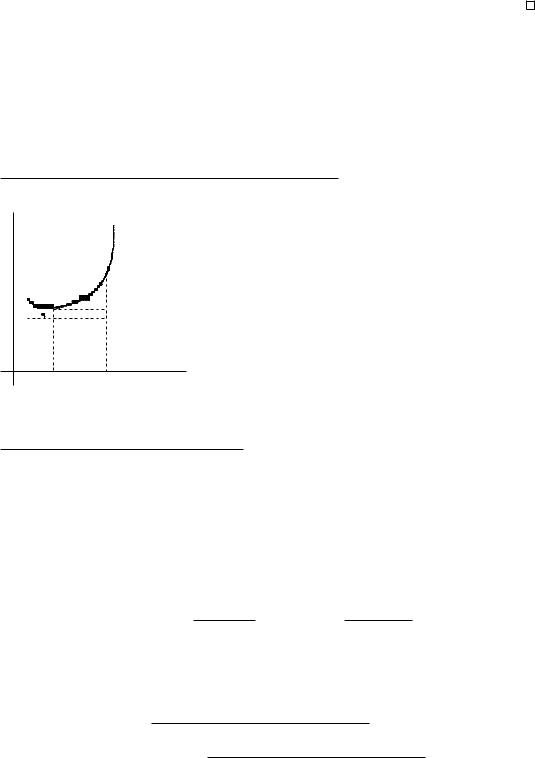
Определение 5.3. Функция y = f(x) называется дифференцируемой в
точке x0, если она определена в окрестности U(x0) и
y = f(x0 + x) − f(x0) = A x + o(Δx), x → 0, |
(5.1) |
39
где A – некоторая постоянная, не зависящая от |
x. |
Главный линейный член приращения функции A |
x называется диффе- |
ренциалом функции f (дифференциалом первого порядка, или первым дифференциалом) и обозначается символом dy или df(x0).
Лемма 5.3. Для того, чтобы функция y = f(x) имела производную в точке x0, необходимо и достаточно, чтобы она была дифференцируема в этой точке.
Доказательство. Необходимость. Пусть существует f0(x0) = lim |
y |
|
. Тогда |
y |
|
= f0(x0)+ |
|
x |
x |
||||||
x→0 |
|
|
|||||
ε(Δx), где ε(Δx) → 0 при x → 0, или y = f0(x0) · x + o(Δx), |
x → 0. Так как f0(x0) не |
||||||
зависит от x, то это означает дифференцируемость f в точке x0, причем постоянная A в дифференциале функции равна f0(x0).
Достаточность. Пусть f дифференцируема в точке x0, т. е. y = A · x + o(Δx). Тогда
lim |
y |
|
= A, т. е. производная f0(x0) существует и равна A. |
|
x |
||||
x→0 |
|
|||
Из определения 5.1 дифференциала и равенства A = f0(x0), доказанного в лемме, следует df(x0) = f0(x0)Δx.
По соглашению x обозначается через dx, что не противоречит выражению dx = x0 x =
x. Поэтому dy = f0(x)dx (или df = f(x)dx). Отсюда следует f0(x) = dxdy , т. е. производная функции f в точке x равна отношению дифференциала функции f к дифференциалу
независимой переменной x. Следует иметь в виду, что дифференциал dx независимой переменной не зависит от x, он равен x – произвольному приращению аргумента x. Что же касается дифференциала dy функции y (отличной от x), то он зависит от x и dx.
Геометрический смысл дифференциала в точке |
||||||
y |
6 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
α |
B |
|
|||
|
|
q |
|
|
||
|
q |
|
q |
|
|
|
|
|
q |
|
|
||
|
A |
|
|
|
|
|
|
|
D |
|
|
||
|
|
|
|
|
||
|
x |
x+Δx |
- |
|||
0 |
x |
|||||
|
|
|
|
|||
y = BC + CD, где CD = f0(x) · x = dy, f0(x) = tg α
CD = dy – главный линейный член приращения y, BC = o(Δx).
Техника дифференцирования
1.(Арифметические операции) Пусть функции f и g дифференцируемы в точке x, тогда в точке x дифференцируемы функции f ± g, fg, f/g (если g(x) 6= 0), причем
(f ± g)0 = f0 ± g0 |
, |
d(f ± g) = df ± dg, |
|||||||||||
(f g)0 |
= f0g + fg0 |
, |
d(f g) = gdf + fdg, |
||||||||||
|
f |
|
0 |
= |
f0g − fg0 |
, d |
f |
|
= |
dfg − fdg |
. |
||
g |
|
|
|
|
|
||||||||
|
|
g2 |
|
|
g |
|
g2 |
||||||
Доказательство. Для доказательства достаточно использовать определение производных и известные арифметические свойства пределов:
(f(x) ± g(x))0 = lim
h→0
(f(x + h) ± g(x + h)) − (f(x) ± g(x)) = h
(f(x + h) − f(x)) ± (g(x + h) − g(x)) = f0(x) ± g0(x), h
40
