
Semestr1-hyper1
.pdf
Определение 3.3. (Определение Коши) Число α называется пределом функции f(x) в точке a, если:
ˇ |
(3.1) |
ε > 0 δ > 0 : x E ∩ Uδ(a) (|f(x) − α| < ε). |
Используемые обозначения для предела: α = lim f(x) или f(x) → α при
x→a
x → a. Подчеркнем, что понятие предела функции в точке a вводится только для предельных точек a области определения функции, при этом функция может быть и не определена в точке a.
Лемма 3.1. Определения 1 и 2 эквивалентны.
Доказательство. Пусть α = lim f(x) в смысле определения 3.2, а (3.1) не выполняется.
x→a
Это значит, что существует хотя бы одно ε > 0 (обозначим его ε0), такое, что для любого
∩ ˇ | − | ≥
δ > 0 существует x E Uδ(a), для которого f(x) α ε0. Будем брать в качестве δ числа
∩ ˇ \{ }
вида δ = 1/n, n = 1, 2, 3, . . . , и для каждого из них найдем точку xn E U1/n(a) E a , для которой |f(xn) − α| ≥ ε0. Но это противоречит определению 3.2.
Пусть теперь α = lim f(x) в смысле определения 3.3, т.е. справедливо (3.1). Возьмем
x→a
произвольную последовательность {xn} E \ {a}, сходящуюся к a. Подберем натуральное число N так, чтобы |xn−a| < δ для любых n > N. Тогда, согласно условию (3.1) |f(xn)−α| <
ε для любых n > N, т. е. f(xn) → α. Это означает, что α = lim f(x) и в смысле определения
x→a
3.2.
Свойства пределов функций
1. Если определена в некоторой проколотой окрестности ˇ точки , f(x) V (a) a
то существует ˇ , в которой ограничена.
U(a) f(x)
Доказательство. Так как lim f(x) = α, то для ε = 1 существует δ > 0 такое, что
x→a
если 0 < |x − a| < δ, то |f(x) − α| < 1. Таким образом, для некоторой проколотой
ˇ |
|f(x)| − |α| ≤ |f(x) − α| < 1, |
окрестности U(a) точки a справедливы неравенства |
|
ˇ |
|
откуда |f(x)| < |α| + 1 для x U(a). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˇ |
|
|
|
|
|
|
|
|
2. Если f(x) определена в некоторой проколотой окрестности V (a) точки a |
||||||||||||||||||||||||||||||||||||||||||
lim f(x) = α = 0 |
|
|
|
|
|
|
|
|
|
Uˇ |
(a) |
|
|
|
|
|
|
|
|
|
|
f(x) > |
|α|, x |
|
|
Uˇ |
(a) |
|
||||||||||||||
и x a |
|
|
|
6 |
|
, то существует |
|
|
|
такая, что |
| |
|
| |
|
2 |
|
|
|
|
|
|
. |
||||||||||||||||||||
→ |
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При этом f(x) > |
если α > 0 и f(x) < |
если α < 0. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
lim f(x) = α = 0 |
|
ε = |
|α| > 0 |
|
|
|
|
|
|
|
Uˇ |
(a) |
|
|
|
|||||||||||||||
Доказательство. Пусть x |
→ |
a |
6 |
|
и |
|
|
|
2 |
|
|
|
. Тогда существует |
|
|
|
|
такая, |
||||||||||||||||||||||||
|
|
|
Uˇ (a) : |
|
f(x) |
|
|
|
|
|α| |
|
|
f(x) > |α| |
|
|
α > 0 |
|
f(x) > |
|
α |
|
|
|
|||||||||||||||||||
|
x |
|
|
|
|
α |
|
< |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
что |
|
|
|
| |
α |
|
− |
|
| |
|
|
2 |
|
, поэтому | |
|
|
| |
|
2 |
|
. Если |
|
|
, то |
|
|
|
|
|
2 |
, а если |
|||||||||||
α < 0, то f(x) < |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. (Арифметические свойства) Пусть f(x) и g(x) определены в некоторой
проколотой окрестности ˇ точки . Тогда справедливы равенства:
V (a) a
lim(f(x) |
± |
g(x)) = lim f(x) |
lim g(x), |
|
|||||||||||||
x→a |
|
|
|
x→a |
|
|
|
|
± x→a |
|
|||||||
lim f(x) |
· |
g(x) = lim f(x) |
· |
lim g(x), |
|
||||||||||||
x |
→ |
a |
|
|
|
|
x |
→ |
a |
|
|
|
x |
a |
(3.2) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|||
|
|
|
f(x) |
|
|
|
lim f(x) |
|
|
|
|
|
|
|
|
||
lim |
|
= |
x→a |
|
, |
(lim g(x) = 0), |
|
||||||||||
g(x) |
|
|
|||||||||||||||
x |
a |
|
|
lim g(x) |
|
x |
→ |
a |
|
6 |
|
||||||
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x→a
в том смысле, что если определены правые части, то определены левые, и они равны.
21

Доказательство. Пусть определены правые части равенств (3.2): lim f(x) = α и
x→a
lim g(x) = β. Пусть {xn} – произвольная последовательность чисел xn 6= a, сходя-
x→a
щаяся к a. Тогда lim f(xn) = α, lim g(xn) = β. Но для числовых последовательностей {f(xn)} и {g(xn)} арифметические свойства доказаны ранее, именно,
|
|
lim(f(xn) ± g(xn)) = lim f(xn) ± lim g(xn), |
|
||||
|
|
lim f(xn) · g(xn) = lim f(xn) · lim g(xn), |
|
||||
lim |
f(xn) |
lim f(xn) |
lim g(x) = 0). |
||||
|
|
|
|
||||
g(xn) |
= lim g(xn) , (lim g(xn) 6= 0, так как |
||||||
|
x→a |
6 |
|||||
Поскольку эти равенства выполняются для любой последовательности xn → a, xn 6= a, то равенства (3.2) также справедливы. 
4.Пусть f(x), g(x) и ϕ(x) определены в некоторой окрестности точки a, за исключением, может быть, самой точки a, и удовлетворяют неравенствам
f(x) |
≤ |
ϕ(x) |
≤ |
g(x) |
|
lim f(x) = lim g(x) = α |
lim ϕ(x) = α |
. |
|||
|
|
|
. Пусть x a |
x |
→ |
a |
. Тогда x a |
||||
|
|
|
|
|
|
→ |
|
|
→ |
|
|
Доказательство. Пусть xn → a, |
xn 6= a – произвольная последовательность. При |
||||||||||
достаточно больших n f(xn) |
≤ ϕ(xn) ≤ g(xn). Так как при этом lim f(xn) = |
α и |
|||||||||
lim g(xn) = α, то lim ϕ(xn) = α. В силу того, что {xn} является произвольной последовательностью, сходящейся к a, утверждение теоремы доказано. 
Первый замечательный предел
lim |
sin x |
= 1. |
|
x→0 |
x |
|
|
y 6 |
N |
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
TT |
|
|
|
x |
T |
- |
|
TM |
||
0 |
|
|
x |
Доказательство. Рассмотрим часть единичного круга. Из обозначений на рисунке легко видеть, что площадь 4AOM < площади сектора OAM < площади 4OMN, т. е.
|
|
|
1 |
sin x < |
1 |
x < |
1 |
tg x |
||||||||
|
|
2 |
2 |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(здесь x – радианная мера AOM). Отсюда |
|
|
|
|
|
|
|
|
|
|
||||||
|
sin x < x < tg x 1 < |
x |
< |
|
1 |
|
при x (0, π/2). |
|||||||||
|
|
|
|
|
|
|||||||||||
|
sin x |
cos x |
||||||||||||||
Поскольку lim cos x = 1, то lim |
sin x |
= lim |
|
x |
|
= 1. |
|
|
||||||||
x |
|
|
|
|
|
|
|
|||||||||
x→0 |
x→0 |
x→0 sin x |
|
|
|
|
||||||||||
3.3Критерий Коши существования конечного предела функции
Пусть f – некоторая числовая функция, определенная на множестве E, и a – предельная точка E.
Теорема 3.2. Для того, чтобы существовал конечный предел lim f(x), необ-
x→a
ходимо и достаточно выполнения следующего условия Коши:
ˇ |
0 |
, x |
00 |
ˇ |
0 |
00 |
)| < ε. |
(3.3) |
ε > 0 U(a) : |
x |
|
U |
(a) ∩ E (|f(x |
) − f(x |
Доказательство. Необходимость. Пусть существует конечный предел lim f(x) = α. Тогда
ˇ |
ˇ |
x→a |
любого ε > 0 существует U |
(a) такая, что для x U |
(a) ∩E : |f(x) −α| < ε/2. Таким образом, |
0 00 ˇ ∩ | 0 − 00 | ≤ | 0 − | | 00 − |
если x , x U(a) E, то f(x ) f(x ) f(x ) α + f(x ) α < ε, т. е. выполняется условие Коши (3.3).
22

Достаточность. Пусть выполнено (3.3). Возьмем произвольную последовательность {xn}, xn E \ {a}, сходящуюся к a. Тогда, согласно критерию Коши для числовой последова-
ˇ
тельности, найдется N N такое, что для любых n, m > N : xn, xm U(a). Но тогда |f(xn) − f(xm)| < ε при любых n, m > N, т. е. числовая последовательность {f(xn)} удовлетворяет условию Коши и, следовательно, имеет предел. Таким образом, мы доказали следующее свойство рассматриваемой функции: для любой сходящейся к a последователь-
ности xn 6= a существует lim f(xn). Для завершения доказательства существования lim f(x)
x→a
необходимо показать, что lim f(xn) будет один и тот же для любой последовательности
xn → a, xn 6= a. Пусть xn → a, x0n → a (xn, x0n 6= a, n = 1, 2, . . .). По доказанному выше, существуют lim f(xn) и lim f(x0n). Предположим, что lim f(xn) = α, lim f(x0n) = α0. Составим
новую числовую последовательность: {x1, x01, x2, x02, . . .}. Очевидно, что x00n → a. Но тогда должен существовать lim f(x00n), что возможно только тогда, когда α = α0. Итак, для любой последовательности x→a, xn 6= a, существует lim f(xn) = α, что означает: существует
lim f(x) = α.
x→a
3.4Обобщения и модификации понятия предела функции в точке
Пределы в бесконечных точках и бесконечные пределы
Понятия предела функции можно обобщить на случай, когда α – несобственная точка.
Определение 3.4. lim f(x) = ∞, если a – предельная точка множества E
x→a
и
|
lim f |
x |
M > 0 U(a) : x Uˇ (a) \ E (|f(x)ˇ| > M). |
f |
x |
|
> |
|
|||
Если |
) = ∞ и в некоторой окрестности |
U a |
) функция |
) |
0 |
||||||
x a |
( |
|
( |
( |
|
|
|||||
|
→ |
|
|
|
|
|
|
|
|
|
|
(соответственно f(x) < 0), то пишут: lim f(x) = +∞ (соответственно
x→a
lim f(x) = −∞).
x→a
Определение 3.5. Число α называется пределом функции f в ∞ (обозна-
ˇ ∞
чение lim f(x) = α), если f(x) определена в некоторой окрестности U( ) и
x→∞
для любой сходящейся к ∞ последовательности {xn} справедливо f(xn) → α. Последнее условие можно заменить эквивалентным условием:
ˇ |
ˇ |
|
|
|
ε > 0 U(∞) : x U(∞) (|f(x) − α| < ε). |
||||
Аналогично определяются lim |
f(x) |
и lim |
f(x). Единственное отличие |
|
x→+∞ |
|
x→−∞ |
ˇ |
ˇ |
состоит в том, что используются, соответственно, U(+∞) и U(−∞)
Односторонние пределы
Пусть f – некоторая числовая функция, определенная на множестве E.
Определение 3.6. Число α R называется пределом функции в точке a
справа (обозначение lim f(x) = α), если a – предельная точка множества
x→a+0
E ∩ (a, +∞) и
для любой последовательности {xn}, xn > a, xn E : xn → a f(xn) → α.
(3.4)
Условие (3.4) эквивалентно следующему условию:
для любой окрестности V (α) δ > 0 : x E ∩(a, a+δ) : f(x) V (α). (3.40)
Определение 3.7. Число α R называется пределом функции в точке a
слева (обозначение lim f(x) = α), если a – предельная точка множества
x→a−0
E ∩ (−∞, a) и
для любой последовательности {xn}, xn < a, xn E : xn → a f(xn) → α.
(3.5)
23
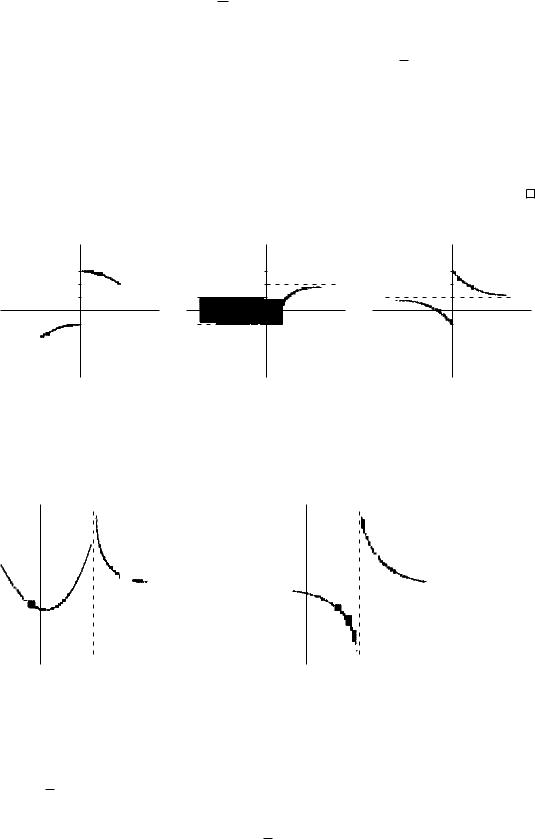
Условие (3.5) эквивалентно следующему условию:
для любой окрестности V (α) δ > 0 : x E ∩(a−δ, a) : f(x) V (α). (3.50)
Лемма 3.2. Пусть f(x) определена в некоторой проколотой окрестности
ˇ
U(a) точки a. Предел lim f(x) в R существует тогда и только тогда, когда
x→a
существуют оба односторонних предела lim f(x) и lim f(x) и они равны.
x→a−0 x→a+0
Доказательство. Необходимость. Пусть существует lim f(x) = α R, т. е.
x→a
для любой окрестности V (α) δ > 0 : x E ∩ (a − δ, a) ∩ (a, a + δ)
Тогда очевидно выполнены условия (3.40) и (3.50), так что существуют
α
Достаточность. Пусть существуют lim f(x) = lim f(x) = α, т. е. выполнены условия
x→a−0 x→a+0
(3.40) и (3.50). Выбирая в этих условия одинаковые δ, получим как следствие условие (3.6),
т.е. существование двухстороннего предела lim f(x) = α.
x→a
y 6 |
y |
6 |
y 6 |
3 |
3 |
|
3 |
2 |
2 |
- |
2I |
|
1 |
|
1 |
|
- |
|
|
1 |
|||
-0 |
- |
|
- |
R0 |
- |
x |
0 |
x |
x |
||
−1 |
−1 |
−1 |
|
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
|
|
|
|
|
|
|
Рис. 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
lim |
f(x) = 2, |
|
|
lim f(x) = |
− |
1 |
|
|
|
|
|
|
|
|
|
|
lim f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
Рис. 1. x→0+0 |
|
|
|
|
|
|
|
|
|
|
x→0−0 |
|
(существуют), x→0 |
|
|
|
|
|
|
|
|
|
|
|
– не существует. |
|
||||||||||||||||||||||||||||||||||||||
|
Рис. 2. |
|
lim |
f(x) = 2 (существует), |
lim f(x) – не существует. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
lim |
|
f(x) = |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim f(x) |
|
|||||||||||||||
|
Рис. 3. |
lim f(x) = 1, |
|
|
|
lim f(x) = 3, |
|
− |
|
(существует), |
– не |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
x |
→ |
0+0 |
|
|
x |
0 |
− |
0 |
|
|
|
|
|
|
|
|
x |
→ |
0 |
|||||||||||||||||||||||||||||||
существует. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
y 6 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
y 6 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
a |
|
|
|
|
x |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 ?
?
x a 0 f(x) = +∞, x a+0 |
−∞ x a 0 |
x a+0 |
−∞ |
|
lim |
lim f(x) = |
lim f(x) = |
lim f(x) = |
|
→ − |
→ |
→ − |
→ |
|
3.5Второй замечательный предел
Ранее было определено число e как предел числовой последовательности: e = lim 1 + n1 n . Теперь мы установим более общий результат:
lim 1 + 1 x = e.
x→∞ x
Очевидно, достаточно доказать это равенство для случаев x → +∞ и x → −∞. Пусть x → +∞. Тогда справедливы неравенства:
|
1 |
|
[x] |
1 |
|
x |
|
1 |
|
[x]+1 |
|
|
1 + |
|
|
|
< 1 + |
|
|
|
< 1 + |
|
|
, |
(3.7) |
[x] + 1 |
|
x |
|
[x] |
||||||||
24
|
1 |
|
[x] |
1 |
|
где [x] – целая часть числа x. Последовательности 1 + |
|
и 1 + |
|||
|
|
||||
[x] + 1 |
[x] |
вые и их пределы равны числу e. Отсюда и из неравенств (3.7) следует lim
x→+∞
Пусть теперь x → −∞. Тогда
[x]+1
– число-
1 + x1 x = e.
x→−∞ |
1 |
|
|
x |
1 |
|
−y |
|
y |
|
y |
|
|
|
|
|
|
|
|
|
|||
x |
|
= y→+∞ 1 − y |
|
y→+∞ y − 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
lim |
1 + |
|
|
|
|
lim |
|
|
|
= lim |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= y→+∞ |
|
1 |
|
y−1 |
· |
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
y − 1 |
|
y − 1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
lim |
|
1 + |
|
|
|
|
|
1 + |
|
|
= e. |
|
3.6Порядок функции. Эквивалентность функций (асимптотика)
Определение 3.8. Функция f имеет порядок функции ϕ на множестве E, или f есть O большое от ϕ на E (обозначение: f(x) = O(ϕ(x)), x E), если
|f(x)| ≤ C|ϕ(x)|, x E,
где C – не зависящая от x постоянная.
Определение 3.9. Пусть функции f и g определены в некоторой проколо-
ˇ
той окрестности U(a) точки a.
Функция f есть "o малое от функции g"при x → a (обозначение f(x) = o(g(x)), x → a), если
f(x) = ε(x)g(x), где функция ε(x) → 0 при x → a.
|
|
g(x) = 0 |
|
ˇ |
f(x) |
= 0. |
||||
|
|
|
U(a) |
lim |
||||||
(если |
|
|
6 |
в |
|
, то эквивалентная запись x→a |
g(x) |
|
|
|
Функция f есть "O большое от функции g(x)"при x → a (обозначение |
||||||||||
|
|
|
|
|
|
|
ˇ |
ˇ |
||
f(x) = O(g(x)), x → a), если существует U(a) такая, что f(x) = O(g(x)), x U(a). |
||||||||||
Функции f(x) и g(x) называются эквивалентными при x → a (обозначение |
||||||||||
|
|
|
|
|
|
|
|
|
|
ˇ |
f(x) ' g(x), x → a), если f и f не равны нулю в некоторой U(a) и если |
||||||||||
lim |
f(x) |
|
= 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x→a g(x) |
|
|
|
|
|
|
|
|||
Лемма 3.3. f(x) ' g(x), x → a, тогда и только тогда, когда f(x) = g(x) + o(g(x)), x → a.
Доказательство. Пусть f(x) ' g(x), x → a и r(x) = f(x) − g(x). Тогда
|
|
|
|
|
|
|
|
|
|
|
|
lim |
r(x) |
= lim |
f(x) |
− |
1 |
= 0, |
|||||
x |
→ |
a g(x) |
x |
→ |
a |
g(x) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
поэтому r(x) = o(g(x)), x→a и, следовательно, f(x) = g(x) + o(g(x)), x → a. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
f(x) |
|
Обратно, пусть f(x) = g(x) + o(g(x)), x → a Тогда |
|
= 1 + o(1), x → a, т. е. f(x) ' |
|||||||||
g(x) |
|||||||||||
g(x), x → a
Лемма 3.4. Если f(x) ' ϕ(x), x → a и функция ψ(x) определена в некоторой
ˇ |
|
U(a), то lim f(x)ψ(x) = lim ϕ(x)ψ(x) в том смысле, что если определена одна |
|
x→a |
x→0 |
из частей равенства, то определена и другая и они равны.
Доказательство. Пусть, например, определена правая часть равенства. Тогда lim f(x)ψ(x) =
x→a
lim f(x)
x→a ϕ(x)
· ϕ(x)ψ(x) = lim ϕ(x)ψ(x).
x→a
Примеры.
1.sin x ' x, x → 0 (эквивалентная запись 1-го замечательного предела).
2.1 − cosx ' 12 x2, x → 0. 3. x2 = o(x), x → 0.
4.x = o(x2), x → ∞.
5.x = O(sin x), x → 0.
Упражнения
25

1.Пусть f(x) > g(x) в некоторой проколотой окрестности точки a R и существуют пределы f(x) и g(x) в точке a. Доказать, что lim f(x) ≥ lim g(x). Можно ли последнее
x→a x→a
неравенство заменить на строгое?
2.Является ли произведение двух монотонных функций монотонной функцией?
3.Пусть lim f(x) 6= 0, а lim g(x) не существует. Доказать, что lim f(x)g(x) не суще-
x→x0 |
x→x0 |
|
|
|
|
x→x0 |
|
ствует. |
|
|
|
|
|
|
|
4. Пусть lim f(x) = 0, а |
lim g(x) не существует. Когда существует lim f(x)g(x)? |
||||||
x→x0 |
x→x0 |
|
|
|
|
x→x0 |
|
5. Функции f и g неотрицательны. Доказать, что |
|
|
|
||||
|
sup(f(x)g(x)) ≤ sup f(x) · sup g(x), |
||||||
|
x A |
x A |
x A |
||||
|
inf (f(x)g(x)) |
inf f(x) |
inf g(x). |
||||
|
x |
|
A |
|
· x |
|
A |
|
|
≥ x A |
|
||||
Можно ли здесь знаки неравенства заменить на равенство?
26
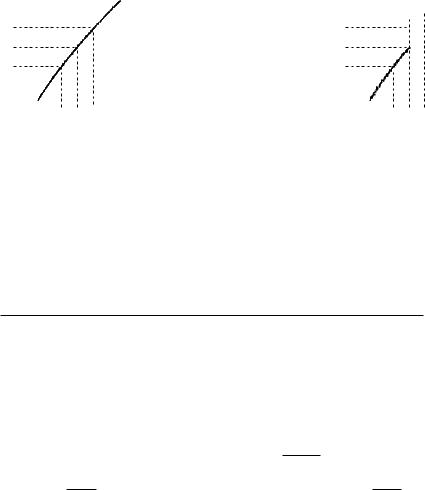
§4 Непрерывные функции
4.1Определение и основные свойства функций, непрерывных в точке
Определение 4.1. Функция f называется непрерывной в точке a, если
она определена в некоторой окрестности U(a) точки a и lim f(x) = f(a).
x→a
Мы имеем два эквивалентных определения предела функции в точке, поэтому данное определение можно развернуть двумя эквивалентными способами:
Определение 4.2. Функция f называется непрерывной в точке a, если она определена в некоторой U(a) точки a и выполнено одно из следующих условий:
ε > 0 δ > 0 : x (a − δ, a + δ) (|f(x) − f(a)| < ε), |
(4.1) |
для любой последовательности {xn} : xn → a f(xn) → f(a). |
(4.2) |
Если функция не является непрерывной в точке a, то говорят, что она разрывна в точке a. В случае, когда функция определена на U(a), разрывность в точке a можно определить на языке (ε, δ) следующим образом:
ε > 0 : δ > 0 x (a − δ, a + δ) (|f(x) − f(a)| ≥ ε).
y |
|
6 |
|
|
|
|
y |
|
6 |
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
f(a)+ε |
|
|
|
|
|
f(a)+ε0 |
|
|
|
|
|
|
|
|
|
r |
|
|||
) |
|
|
|
|
|
f(a) |
|
|
|
|
|
|
|
|
|
|
||||
f(af)(aε |
|
|
|
|
|
f(a) |
ε0 |
|
|
|
|
|
|
|
|
|
|
|||
− |
|
|
|
- |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
a−δ a a+δ |
x |
|
0 |
|
|
|
|
|
|
|
a−δ a a+δ |
x |
|||||
|
|
|
|
Рис. 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2. |
|
На рис. 1 изображена непрерывная кривая ("непрерывность" понимается в интуитивном смысле – кривую можно начертить, не отрывая карандаша от бумаги). Пусть эта кривая является графиком некоторой функции f(x). Тогда ε > 0 δ > 0 x (a −δ, a + δ) (|f(x) − f(a)| < ε) (все это видно на рисунке) и, следовательно, математическое определение непрерывности функции отвечает интуитивному понятию непрерывности кривой.
На рис. 2 изображена разрывная кривая, состоящая из двух кусков. Разрыв имеет место в точке a. На рисунке видно, что существует ε0 > 0 такое, что для любых δ > 0 существует x (a − δ, a + δ) такое, что |f(x) − f(a)| ≥ ε0. Таким образом, разрывному графику соответствует разрывная функция.
Основные свойства функций, непрерывных в точке
Перечисленные ниже свойства являются простым следствием соответствующих свойств пределов функций.
1. Если функция f непрерывна в точке, то она ограничена в некоторой окрестности этой точки.
2. Если функция f(x) непрерывна в точке a и f(a) 6= 0, то существует
окрестность U(a), в которой |f(x)| > |f(a)|. Более того, если f(a) > 0, то
2
f(x) > f(2a), x U(a), а если f(a) < 0, то f(x) < f(2a), x U(a).
3.(арифметические свойства). Пусть функции f и g непрерывны в точке a, тогда в точке a непрерывны также функции: f(x) ± g(x), f(x) · g(x), f(x)/g(x), если g(x) 6= 0.
27

Лемма 4.1. (непрерывность суперпозиции функций) Если функция ϕ(x) непрерывна в точке a и функция f(y) непрерывна в точке b = ϕ(a), то функция F (x) = f(ϕ(x)) – непрерывна в точке a.
Доказательство. Зададим ε > 0. Вследствие непрерывности функции f в точке b существует δ1 > 0 такое, что f(y) определена на интервале (b−δ1, b+ δ1) и выполняется неравенство:
|f(y) − f(b)| < ε, если |y − b| < η.
А в силу непрерывности функции ϕ в точке a существует δ > 0 такое, что ϕ(x) определена на интервале (a − δ, a + δ) и
|ϕ(x) − ϕ(a)| < η для |x − a| < δ.
Из этих двух неравенств при y = ϕ(x) и b = ϕ(a) следует
|f(ϕ(x)) − f(ϕ(a))| < ε для |x − a| < δ,
что и означает непрерывность F (x) = f(ϕ(x)) в точке a.
Определение 4.3. Обозначим |
f(a + 0) = |
|
lim |
f |
( |
x |
) и |
f |
( |
a |
lim |
|
f(x) |
. |
|
|
x |
→ |
a+0 |
|
|
|
|
− 0) = x a |
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
→ − |
|
|
|
|
Функция f называется непрерывной справа в точке a, если существует f(a+ 0) = f(a). Функция f называется непрерывной слева в точке a, если существует f(a − 0) = f(a).
Лемма 4.2. Если f непрерывна в точке a тогда и только тогда, когда она непрерывна как справа, так и слева в точке a.
Доказательство. Следует из леммы 3.2 параграфа §3.
4.2Классификация разрывов
Определение 4.4. Если функция f не является непрерывной в точке a, но
существует конечный предел lim f(x), то говорят, что f имеет устрани-
x→a
мый разрыв в точке a.
y |
|
6 |
|
|
|
|
y |
|
6 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
f(a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
α |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
- |
0 |
|
|
a |
x |
0 |
|
|
a |
x |
|||
|
|
|
Рис. 1. |
|
|
|
|
|
|
Рис. 2. |
|
|
|
|
lim |
f(x)=lim f(x)=α |
|
|
|
|
|
lim |
f(x)=lim f(x)=α |
|
|
|
|
x→a+0 |
x→a−0 |
|
|
|
|
|
x→a+0 |
|
x→a−0 |
|
|
|
f(x) - не определена в точке a |
|
|
|
|
f(a) 6= α |
|
||||
В обоих случаях lim f(x) существует, но f разрывна в a, так как (см. рис. 1) f – не определена
x→a
в a и (см. рис. 2) f(a) 6= α = lim f(x). Разрывы функций в точке a легко устраняются. В первом
x→a
случае f нужно доопределить в точке a, а во втором – видоизменить, положив f(a) = lim f(x) = α.
x→a
Определение 4.5. Точка a называется точкой разрыва 1-го рода для
функции |
f |
, если существуют конечные пределы |
f |
|
a |
lim |
f(x) |
и |
f(a |
− |
|
|
( |
|
+ 0) = x→a+0 |
|
|
0) = lim f(x) и они не совпадают.
x→a−0
Если функция определена в точке a и f(a + 0) = f(a), то функция называется непрерывной справа. Если же f(a − 0) = f(a), то функция называется непрерывной слева.
28

Примеры графиков функций, имеющих разрыв 1-го рода в точке a.
|
y |
|
6 |
|
|
|
|
y |
|
6 |
|
|
y |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
a |
x |
0 |
|
a |
x |
0 |
|
a |
x |
|||||
|
|
|
|
Рис. 1. |
|
|
|
|
|
Рис. 2. |
|
|
|
|
Рис. 5. |
|
|
|
|
|
|
f(a+0)6=f(a), |
|
|
|
|
|
f(a+0)6=f(a), |
|
|
|
|
f(a+0)6=f(a−0), |
|
|
|
|
|
|
f(a−0)6=f(a), |
|
|
|
|
|
f(a−0)=f(a), |
|
|
|
|
f не определена в a. |
|
|
|
|
|
|
f - разрывна справа и слева. |
|
|
|
f - разрывна справа и |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
непрерывна слева. |
|
|
|
|
|
|
|
Определение 4.6. Если f определена в некоторой проколотой окрестности
ˇ
U(a) и имеет разрыв в точке a, не являющийся устранимым разрывом или разрывом 1-го рода, то она имеет в a разрыв 2-го рода.
Разрыв второго рода может быть бесконечным или конечным. Функция f имеет бесконечный разрыв в точке a, если она непрерывна в любой точке
достаточно малой окрестности ˇ и не ограничена в . Например,
U(a) U(a) f(x) = tg x имеет бесконечный разрыв в точках xk = π2 + kπ, k Z.
В то же время, функция f(x) = sin x1 (x R, x 6= 0) ограничена и непре-
рывна во всех точках, кроме точки 0, где она имеет разрыв второго рода, поскольку в этой точке не существуют оба односторонних предела.
4.3Свойства функций, непрерывных на отрезке
Определение 4.7. Функция называется непрерывной на отрезке [a, b], если она непрерывна на (a, b), непрерывна слева в точке b и непрерывна справа в точке a.
Теорема 4.1. (1-ая теорема Вейерштрасса) Если f непрерывна на отрезке
[a, b], то она ограничена на [a, b].
Доказательство. Допустим, что f не ограничена на [a, b]. Тогда для любого n N существует xn [a, b] такое, что |f(xn)| > n. Последовательность {xn} ограничена, поэтому согласно теореме Больцано-Вейерштрасса она содержит сходящуюся подпоследовательность {xnk } : xnk → ξ, причем ξ [a, b] в силу замкнутости отрезка. Так как f непрерывна на [a, b],
то lim f(xnk ) = f(ξ). С другой стороны, |f(xnk )| > nk, т. е. последовательность {f(xnk )}
k→+∞
не может иметь конечного предела. Полученное противоречие доказывает утверждение.
Теорема 4.2. (2-ая теорема Вейерштрасса) Если f непрерывна на отрезке
[a, b], то она достигает на [a, b] своих точных граней, т. е. существуют
точки |
ξ |
[ |
a, b |
] и |
η |
[ |
a, b |
], для которых sup |
f |
( |
x |
) = |
f |
( |
ξ |
) |
, |
|
inf |
f(x) = f(η) |
|
|
|
|
|
|
|
|
|
|
x |
|
[a,b] |
. |
|||||||||
|
|
|
|
|
|
|
|
x [a,b] |
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. По теореме 4.1 непрерывная на [a, b] функция ограничена, поэтому имеет конечные верхнюю sup f(x) = M и нижнюю inf f(x) = m грани. В силу определения
x [a,b] |
x [a,b] |
sup для любых n N существует xn [a, b] такое, что
1 |
< f(xn) ≤ M. |
(4.3) |
M − n |
29

Из ограниченной последовательности {xn} выделим сходящуюся подпоследовательность:
xnk → ξ [a, b]. Так как f(x) непрерывна на [a, b], то lim f(xnk ) = f(ξ). А из (4.3) следует
k→+∞
1 |
< f(xnk ) ≤ M, поэтому klim f(xnk ) = M. Но f(xnk ) может сходиться только к |
||
M − |
|
|
|
n |
|
||
|
|
k |
→∞ |
одному пределу, поэтому M = f(ξ). Аналогично доказывается другая часть теоремы.
Замечание 4.1. Очевидно, что f(ξ) это максимальный элемент множества значений функции {y = f(x)| x [a, b]}, поэтому f(ξ) = sup f(x) =
|
|
x [a,b] |
max f(x). Аналогично, f(η) = |
inf |
f(x) = min f(x). |
x [a,b] |
x [a,b] |
x [a,b] |
Замечание 4.2. Как видно из доказательств теорем Вейерштрасса, по существу использовано лишь следующее свойства отрезка: из любой последовательности его точек можно выбрать сходящуюся подпоследовательность, при этом предел этой подпоследовательности принадлежит отрезку. Это свойство служит определением компактного множества (компакта), поэтому результаты теорем могут быть обобщены следующим образом: если функция f(x) непрерывна на компакте, то она ограничена и достигает своих максимального и минимального значений. В R компактом является любое ограниченное и замкнутое множество.
Теорема 4.3. (теорема Больцано-Коши о промежуточных значениях) Если f
непрерывна на отрезке [a, b] и число C лежит между f(a) = A и f(b) = B, то существует число c (a, b) такое, что f(c) = C.
Доказательство. Будем считать для определенности, что A < B. Пусть g(x) = f(x) − C, тогда функция g(x) непрерывна на [a, b] и g(a) < 0 < g(b). Следует доказать, что найдется точка c (a, b) такая, что g(c) = 0.
Построим последовательность вложенных отрезков I1 I2 . . . по следующему правилу. Положим I1 = [a, b] и пусть x1 середина I1. Если g(x1) = 0, то c = x1 и теорема доказана. Пусть g(x1) 6= 0, в качестве I2 возьмем тот из отрезков [a, x1], [x1, b], на концах которого g(x) имеет различные знаки. Если I1 I2 . . . In−1 построены и xn−1 середина In−1, причем g(xn−1) 6= 0, то In – тот из двух подотрезков In−1, на концах которого g имеет различные
|
∞ |
знаки. По лемме о вложенных отрезках существует точка c |
n\ |
In. Докажем, что g(c) = 0. |
|
|
=1 |
Действительно, если мы допустим, что g(c) > 0, то в силу непрерывности g существует окрестность U(c), в которой g(x) > 0. Но In U(c) при достаточно большом n, а так как на концах In функция g(x) принимает разные знаки, то g(x) не может быть положительной во всей окрестности U(c). Аналогично опровергается предположение g(c) < 0. 
Следствие 4.1. Пусть функция f(x) непрерывна на отрезке [a, b] и M =
max f(x), m = |
min f(x). Тогда f(x) принимает все значения из [m, M] и |
x [a,b] |
x [a,b] |
только эти значения.
4.4Равномерная непрерывность. Продолжение по непрерывности
Определение 4.8. Функция f : E → R (E N) называется равномерно непрерывной на E, если
ε > 0 δ > 0 : x, y E (|x − y| < δ |f(x) − f(y)| < ε).
Теорема 4.4. (Теорема Кантора) Если f непрерывна на [a, b], то она равномерно непрерывна на [a, b].
Доказательство. Предположим противное, т.е.
ε > 0 : δ > 0 x, y [a, b] : (|x − y| < δ, но |f(x) − f(y)| ≥ ε).
Будем брать δ = 1/k, k = 1, 2, 3, . . .. Тогда существуют пары чисел xk, yk [a, b] такие, что
|xk − yk| < |
1 |
, но |f(xk) − f(yk)| ≥ ε, k = 1, 2, . . . . |
(4.4) |
k |
30
