
- •1. Рычажный механизм (лист 1)
- •1.1 Структурный анализ механизма
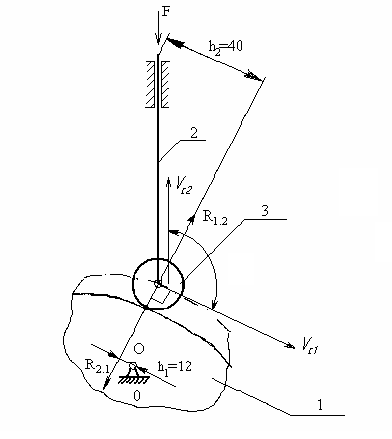
- •1.2 Кинематический анализ механизма
- •1.2.1 Определение линейных скоростей для десятого положения и построения плана скоростей
- •1.2.2 Определение угловой скорости
- •1.2.3 Определение линейных ускорений и построение плана ускорений
- •Значения линейных ускорений точек для 5-го положения.
- •1.3 Силовой расчёт механизма
- •1.3.1 Определение масс звеньев и их веса.
- •1.3.2 Определение сил и моментов инерции
- •1.3.3 Группа Ассура 5-4
- •Группа Ассура 3-2
- •1.3.5 Начальный механизм
- •1.3.6 Определение величины уравновешивающей силы методом рычага н.Е. Жуковского
- •Момент сил инерции Ми.3, звена 3 на рычаге Жуковского заменены парами сил. Значения этой силы определяется из выражения:
- •Значение реакций в кп и уравновешивающей силы
- •Определение кпд механизма
- •Разбивка передаточного отношения по ступеням
- •Приняли передаточное отношение для рядового механизма [2, стр. 13 ]
- •Геометрический расчёт внешнего эвольвентного зацепления
- •Геометрические параметры эвольвентного внешнего зацепления цилиндрических прямозубых колёс, нарезанных инструментом реечного типа
- •2.6. Расчёт качественных показателей зацепления
- •Расчёт коэффициента удельного скольжения
- •Расчёт коэффициента удельного давления
- •Значения величин удельного скольжения и удельного давления для неравносмещенного зацепления (а)
- •Значения величин удельного скольжения и удельного давления для нулевого зацепления (б).
- •2.6.3 Коэффициент полезного действия
- •Определение частоты вращения всех звеньев механизма
- •Значения частоты вращения всех звеньев
- •2.8 Анализ по результатам профилирования
- •Томский политехнический университет
- •3. Кулачковый механизм
- •3.1 Синтез и анализ кулачкового механизма
- •3.2 Определение размеров, профилирование кулачкового механизма
- •3.2.1 Масштабы графиков первой производной
- •3.2.3 Масштабы графиков второй производной
- •3.2.4 Построение графика центра изменения угла передачи движения по углу поворота кулачка.
- •С иловой расчёт кулачка механизма (Для положения а4)
- •3.4 Определение координат профиля кулачка аналитическим методом
- •Список литературы
3.4 Определение координат профиля кулачка аналитическим методом
Координаты точек профиля кулачка заданы в полярной системе координат. В этой системе координат с началом в центре вращения кулачка О координаты любой точки Сi определяются двумя параметрами - радиус вектором ri и полярным углом , отсчитываемым от радиус вектора rо в начале профиля ( точка Со)
При этом заданы:
a) закон движения толкателя по углу поворота кулачка или линейное перемещение точки С конца толкателя:
Sc=Sc(φ)
б) начальный радиус кулачка ro;
в) величина и направление смещения e.
Тогда получим:
Радиус
вектор [5, стр. 6]
![]() (1)
(1)
Полярный
угол [5, стр. 6]
![]() (2)
(2)
Здесь
[5, стр. 6]
![]() (3)
(3)
![]() (4)
(4)
В формуле (2) принимаем знак плюс, т.к угол между векторами скорости точек кулачка Vс1 и Vc2, β > 90 0

Для положения 3(данные берём из закона движения толкателя):
e=7,5, S3 =15мм , S0 =13мм, φ3=400
![]()
![]()
![]()
![]()
Для положения 6(данные берём из закона движения толкателя):
e=7,5, S3 =40мм , S0 =13мм, φ3=1010
![]()
![]()
![]()
Для положения 6(данные берём из закона движения толкателя):
e=7,5, S3 =46мм , S0 =13мм, φ3=2400
![]()
![]()
![]()
Сравниваем полученные результаты с числовыми значениями на чертеже. Значение приведены в таблице 3.2
таблица 3.2
Положение |
Радиус – вектор ri ,мм |
Полярный-угол δi Град. |
Ψi град. |
Ψ0 |
|||
расчётное |
с чертежа |
расчётное |
с чертежа |
расчётное |
с чертежа |
||
3 |
28,98 |
2,9 |
55,6 |
56,25 |
14,4 |
15 |
30 |
6 |
56,4 |
56 |
123,4 |
116 |
7,6 |
9 |
30 |
10 |
59,4 |
59 |
266,8 |
260 |
7,2 |
7 |
30 |
Вывод:
Одним из основных достоинств кулачковых механизмов является лёгкость синтеза, то есть получения профиля кулачка с большой степенью точности, удовлетворяющему заданному закону движения толкателя. В кулачковом механизме легко осуществить движение ведомого звена-толкателя с остановками, при непрерывном движении кулачка.
Недостатком является повышенное удельное давление а, следовательно, повышенный износ элементов высшей кинематической пары, что в свою очередь, приводит к искажению закона движения толкателя. Также кулачковый механизм обладает низким КПД, вследствие увеличения угла давления. При КПД примерно равном нулю, кулачковый механизм может заклиниваться. Тогда для устранения возможности заклинивания, ставится условие, чтобы угол давления во всех положениях механизма был меньше критического, при котором КПД=0.
