
- •Введение
- •1. Компоновка элементов ферм
- •2. Определение генеральных размеров
- •3. Элементы кровельного покрытия
- •4. Расчет элементов прогонной кровли
- •5. Определение нагрузок, действующих на ферму
- •6. Определение узловых нагрузок, действующих на ферму
- •7. Определение опорных реакций
- •8. Определение расчетных усилий в стержнях фермы
- •9. Подбор сечений стержней фермы
- •9.1. Общие положения
- •9.2.Определение расчетных длин стержней фермы
- •9.3. Подбор сечений
- •10. Расчет и проектирование узлов фермы
- •10.1. Общие требования к конструированию узлов
- •10.2.Указания по расчету швов
- •10.3. Промежуточные узлы
- •10.4. Опорные узлы
- •10.5. Укрупнительные узлы
- •11. Соединительные прокладки
- •12. Связи по покрытию
- •13. Проверочный расчет стропильной фермы
- •13.1. Проверка фермы на жесткость
- •13.2. Определение конструктивного коэффициента
- •14.Расчетно-пояснительная записка
- •15. Графическая часть проекта
- •Литература
- •Приложение. Таблица 2
- •Приложение. Таблица 3
6. Определение узловых нагрузок, действующих на ферму
Узловая нагрузка зависит от распределенной нагрузки по площади кровли и от величины площади, которую обслуживает узел
Р=gS , (20)
где S=dвt – площадь, обслуживаемая узлом (рис.7,б). Крайний узел фермы,
обслуживает площадь, меньшую в два раза.
Р ассмотрим
определение постоянных узловых нагрузок
на примере фермы с фонарем (рис.7,а)
ассмотрим
определение постоянных узловых нагрузок
на примере фермы с фонарем (рис.7,а)
![]() , (21)
, (21)
![]() . (22)
. (22)
Для узлов, на которые опираются крайние стойки фонаря
![]() .(23)
.(23)
Рис.7
![]() . (24)
. (24)
Узловую снеговую нагрузку получим по формуле
Рсн=РнnS, (25)
где n - коэффициент перегрузки, принимаемый в зависимости от
отношения нормативного собственного веса покрытия gn к
нормативному весу снегового покрова ро:
gn/ро 1 0,8 0,6 0,4
n 1,4 1,5 1,55 1,6
Промежуточные значения принимают по линейной интерполяции.
Ветровая нагрузка
Рв=gнnhфt , (26)
где n - коэффициент перегрузки ветровой нагрузки, принимаемый равным
1,2;
hф- высота бортовой стенки фонаря. Она складывается из высоты
переплетов остекления, имеющие высоту 1250, 1500, 1750 мм, а
также высот борта и карниза фонаря. Борт фонаря (глухая часть
фонаря от кровли до низа остекления) должен иметь высоту
600...800 мм, чтобы остекление не заносило снегом. Суммарная
высота борта и карниза составляет 900...1000 мм.
Ветровая нагрузка, действующая на фонарь, распределяется равномерно между узлами фермы, на которые он опирается.
7. Определение опорных реакций
Опорные реакции находятся при помощи уравнений статики для всех видов загружений в отдельности. Исходя из этого, строятся расчетные схемы фермы для следующих случаев ее загружения:
от действия постоянных нагрузок;
от действия симметрично расположенного снега на обоих скатах кровли;
от действия несимметрично расположенного снега;
от действия ветровой нагрузки;
от действия единичной силы, приложенной в коньковом или подконьковом узле фермы.
При симметрично расположенной на ферме нагрузке реакции опор А и В равны и определяются из уравнения равновесия проекций сил на ось У:
![]() ,
,
где Рi - i-я узловая нагрузка.
При несимметричном расположении нагрузки на ферме наиболее рационально воспользоваться уравнениями равновесия суммы моментов всех сил относительно одной из опор, определив из него реакцию другой опоры:
mА=0 определяем реакцию В;
mв=0 определяем реакцию А;
у = 0 проверяем правильность найденных реакций.
8. Определение расчетных усилий в стержнях фермы
Усилия в стержнях фермы находим при помощи диаграмм Максвелла-Кремоны отдельно для всех видов загружения.
Рассмотрим пример построения диаграммы усилий для случая действия на ферму постоянной нагрузки (рис.8).
В
Рис.8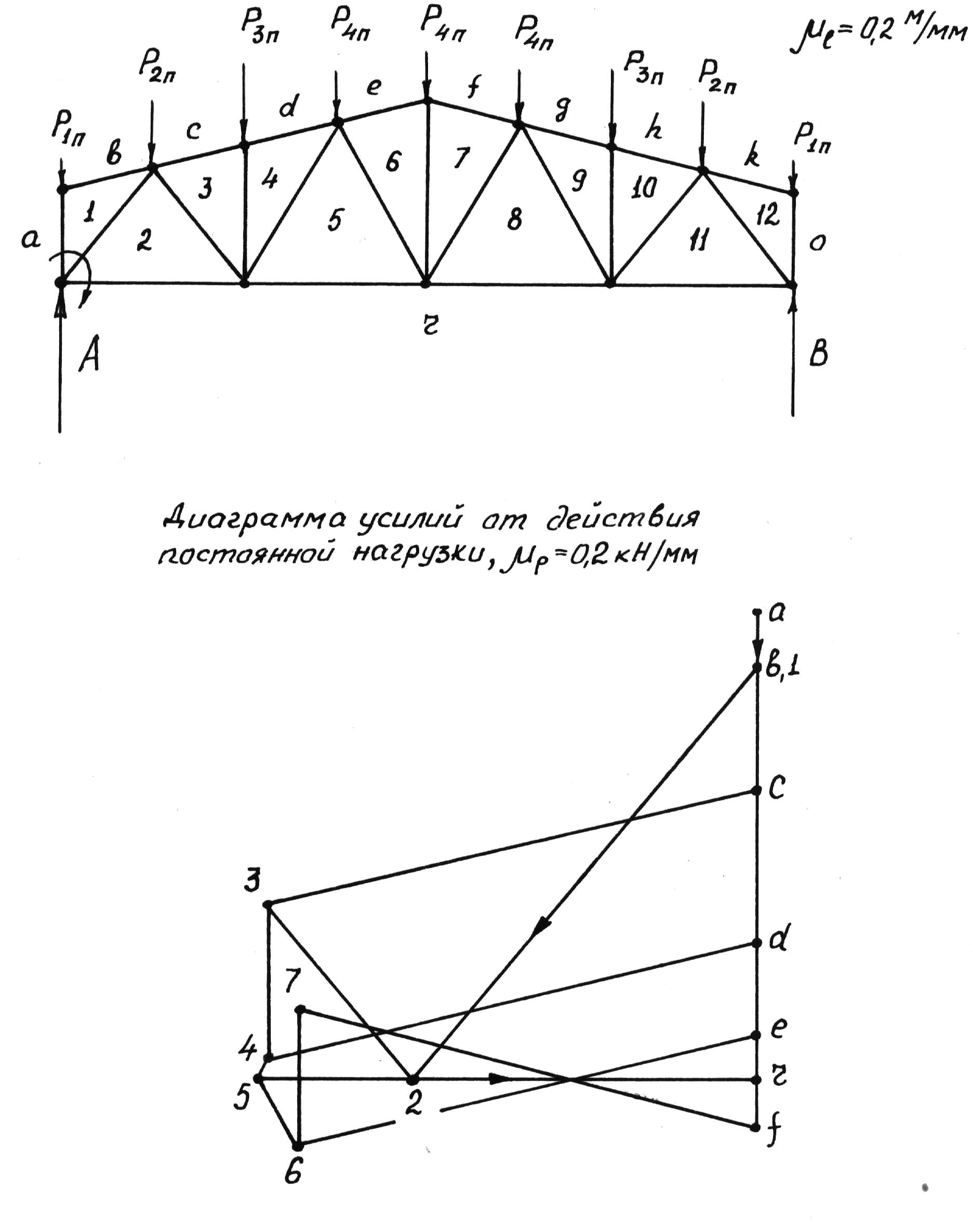
![]() и строим в этом масштабе расчетную схему
фермы. Прикладываем к узлам верхнего
пояса фермы вектора узловых нагрузок
Р1П, Р2П,
Р3П, а к
опорным узлам -вектора опорных реакций.
Обозначаем внешние полигоны буквами
латинского алфавита, а внутренние-арабскими
цифрами, как показано на рис.8. Выбираем
масштаб сил р
и строим в этом масштабе многоугольник
внешних сил (веревочный многоугольник
авсdеf
и т.д). В связи с тем, что загружение фермы
симметрично - достаточно построить
половину силового многоугольника.
и строим в этом масштабе расчетную схему
фермы. Прикладываем к узлам верхнего
пояса фермы вектора узловых нагрузок
Р1П, Р2П,
Р3П, а к
опорным узлам -вектора опорных реакций.
Обозначаем внешние полигоны буквами
латинского алфавита, а внутренние-арабскими
цифрами, как показано на рис.8. Выбираем
масштаб сил р
и строим в этом масштабе многоугольник
внешних сил (веревочный многоугольник
авсdеf
и т.д). В связи с тем, что загружение фермы
симметрично - достаточно построить
половину силового многоугольника.
Построение диаграммы начинаем с узла, в котором не более двух неизвестных. В приведенном случае это узел над опорой А. Обходим узел по часовой стрелке. Из полигона (а) в полигон (в)мы попадаем в вертикальном направлении (ав) на многоугольнике внешних сил. А из полигона (в) в полигон (1) в направлении верхнего пояса. Проводим это направление из точки (в) силового многоугольника. Из полигона (а) в полигон (1) мы должны попасть в вертикальном направлении. Проводим это направление из точки (а) силового многоугольника. Пересечение этих двух направлений даст нам положение точки (1) на диаграмме. Оно совпало с положением точки (в). Далее переходим к опорному узлу. Из полигона (а) в полигон (1) попадаем в вертикальном направлении (положение точки (1) известно), а из полигона (1) в полигон (2) мы должны попасть по направлению опорного раскоса (1-2). Переносим это направление раскоса (1-2) на диаграмму из точки (1). А в полигон (2) из полигона (r) мы должны попасть в горизонтальном направлении. Проводим это направление их точки (r) диаграммы. Пересечение этих двух направлений даст нам положение точки (2) на диаграмме. Обходим следующий узел. Из полигона (с) в полигон (d) мы попадаем в вертикальном направлении. Положения этих точек (с) и (d) нам известны. Из полигона (с) в полигон (3) мы должны попасть по направлению верхнего пояса. Проводим это направление из точки (с) диаграммы. А из полигона (2) в полигон (3) мы попадаем по направлению раскоса (2-3). Это направление проводим из точки (2) диаграммы. Пересечение направления верхнего пояса из точки (с) и направления раскоса (2-3) из точки (2) даст положение точки (3) на диаграмме. И так далее.
Ч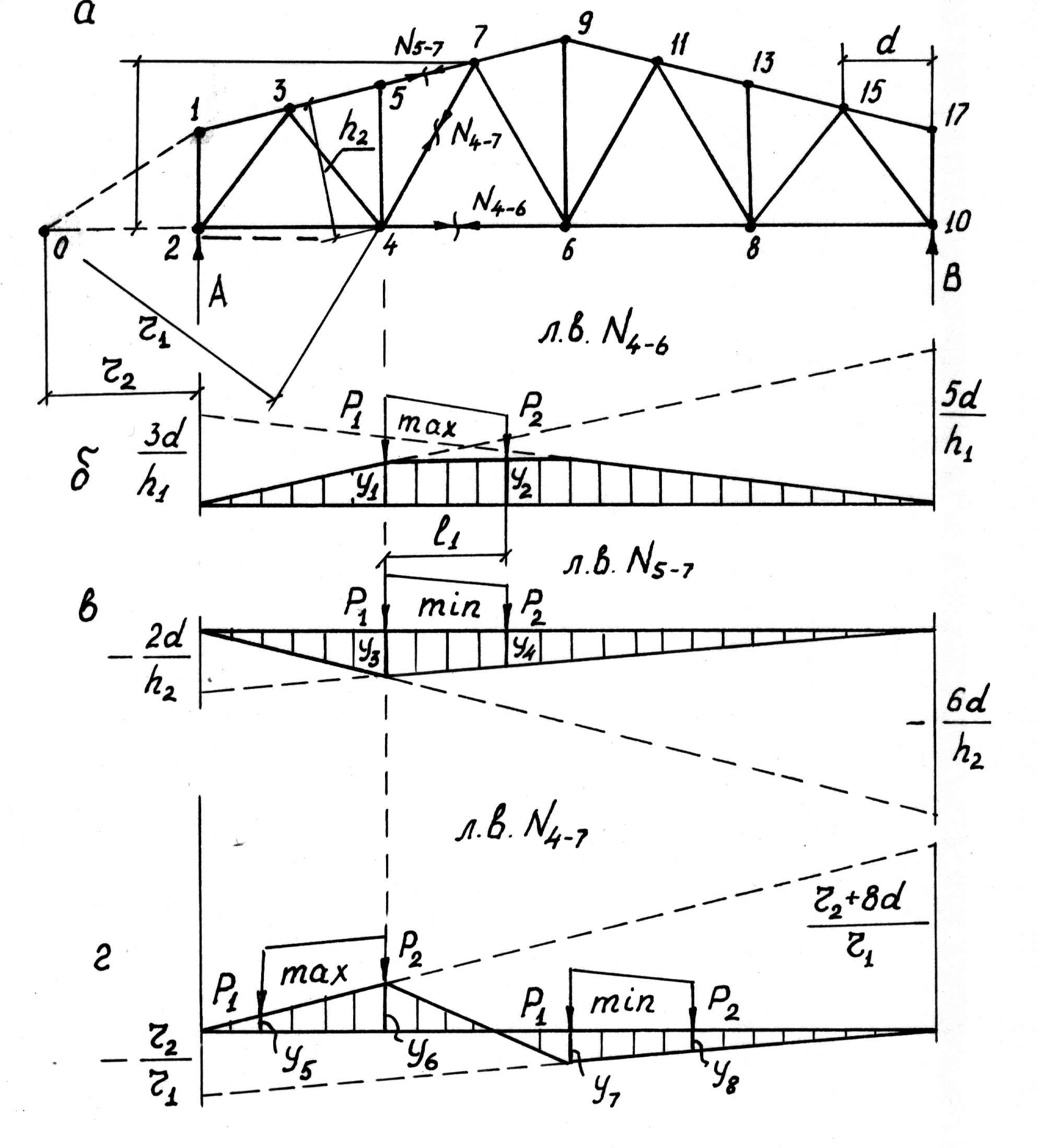 тобы
определить величину усилия в стержне
фермы по диаграмме, необходимо измерить
длину вектора, обозначенного на диаграмме
теми же буквами и цифрами, что и
разграничиваемые данным стержнем
полигоны, и умножить эту длину на масштаб
р.
тобы
определить величину усилия в стержне
фермы по диаграмме, необходимо измерить
длину вектора, обозначенного на диаграмме
теми же буквами и цифрами, что и
разграничиваемые данным стержнем
полигоны, и умножить эту длину на масштаб
р.
З
Рис.9
Для определения максимальных значений (со знаком «+») и минимальных (со знаком «-») усилий в стержнях фермы от действия подвижной нагрузки необходимо построить линий влияния этих усилий, затем загрузить линии влияния подвижной нагрузкой по максимуму и минимуму и, воспользовавшись формулой «Z», найти значения этих усилий:
![]() , (27)
, (27)
где Рi - i-я сосредоточенная сила;
gi - i-я распределенная нагрузка;
Мi - i-й изгибающий момент;
уi - ордината линии влияния под i-й сосредоточенной силой;
i - площадь, ограниченная линией влияния под i-й распределенной нагрузкой;
i - угол наклона линии влияния под i-м изгибающим моментом.
Сосредоточенная сила и распределенная нагрузка - положительны, если они направлены по направлению действия единичной силы. Момент, действующий по направлению часовой стрелки - положительный, против - отрицательный. Тангенс угла наклона линии влияния положителен в первой и третьей четвертях, отрицателен во второй и четвертой.
Например, для стержня (5-r) (N4-6) рис.9 строим линию влияния, рассекая ферму, как показано на рис.9,а. Рассматривая равновесие левой или правой частей фермы, для данного случая удобно воспользоваться уравнением равновесия моментов всех сил относительно точки (7).
Единичную силу Р=1 располагаем слева от рассеченной панели 4-6. Рассматриваем равновесие правой части фермы:
m7=N4-6h1-B5d=0,
откуда
л.в.N4-6=(л.в.В)![]() .
.
Строим левую ветвь линии влияния, откладывая под опорой В ординату 5d/h1 (рис.9,б).
Располагая Р=1 справа от рассеченной панели 4-6 и рассматривая равновесие левой части фермы, запишем:
m7=N4-6h1-À3d=0,
откуда
л.в. N4-6=(л.в.А)![]() .
.
Строим левую ветвь линии влияния, откладывая под опорой А ординату 3d/h1. Перенеся точки 4 и 6 нижней панели фермы на ветви линии влияния и соединяя эти точки передаточной прямой, получаем линию влияния N4-6.
Загружаем
л.в. N4-6
невыгоднейшим образом, например,
подвижной двуосной нагрузкой с весом
осей Р1
и Р2,
расположенных друг от друга на расстоянии
![]() ,
по максимуму, тогда
,
по максимуму, тогда
![]() Р1у1+Р2у2.
Р1у1+Р2у2.
Минимальное
значение
![]() 0,
так как подвижная нагрузка положительна,
а отрицательные ординаты у линии влияния
отсутствуют.
0,
так как подвижная нагрузка положительна,
а отрицательные ординаты у линии влияния
отсутствуют.
Для построения линии влияния N5-7 воспользуемся моментной точкой 4.
Р=1 - слева от рассеченной панели 4-6
m4=N5-7h2+B6d=0,
тогда л.в.
N5-7=
- (л.в.В)![]() .
.
Строим левую ветвь (рис.9,в).
Р=1 - справа от рассеченной панели 4-6.
m4=N5-7h2+À2d=0,
откуда л.в.
N5-7=
- (л.в.А)![]() .
.
Строим
правую ветвь линии влияния N5-7.
При загружении по максимуму
![]() 0,
так как положительные ординаты у линий
влияния N5-7
отсутствуют.
0,
так как положительные ординаты у линий
влияния N5-7
отсутствуют.
На рис.9,в показано невыгоднейшее положение подвижной нагрузки для стержня 5-7 по минимуму.
![]() -
Р1у3-Р2у4.
-
Р1у3-Р2у4.
Для построения линии влияния N4-7 удобно воспользоваться моментной точкой 0 (условно показана на рис.9,а), являющейся пересечением продолжения поясов фермы.
Р=1 располагается слева от рассеченной панели 4-6. Рассматривая равновесие правой части, записываем:
m0=N4-7r1-B(r2+8d)=0,
откуда л.в.
N4-7=
- (л.в.В)![]() .
.
Строим левую ветвь линии влияния (рис.9,г).
Р=1 - справа от рассеченной панели 4-6.
Уравнение равновесия правой части фермы
m0=N4-7r1+Àr2=0,
откуда л.в.
N4-7=
- (л.в.А)![]() .
.
Строим правую ветвь линии влияния. Проецируя точки 4 и 6 на ветви линии влияния и соединяя их проекции передаточной прямой, получаем линию влияния N4-7. На рис.9,г показано загружение линии влияния N4-7 по максимуму и минимуму.
![]() Р1у5+Р2у6,
Р1у5+Р2у6,
![]() -Р1у7-Р2у8.
-Р1у7-Р2у8.
Определив усилия в стержнях фермы от каждого силового воздействия, составим табл. 6 для определения расчетных усилий, сгруппировав стержни фермы с одним наименованием.
Таблица 6
Усилия в стержнях фермы
Наиме-нование группы стерж-ней |
Номер стерж-ня |
Усилие от дей-ствия постоянной нагрузки, кН |
Усилие от действия симмет-рично располо-женного снега, кН |
Усилие от действия несиммет-рично располо-женного снега, кН |
Усилие от действия ветровой нагрузки, кН |
Усилие от действия подвижной нагрузки, кН |
Расчетное усилие, кН |
Усилие от дейс-вия единичной силы |
|||
|
|
|
|
|
|
max |
min |
|
|
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
Верх-ний пояс |
в-1 с-3 |
0 -160 |
0 -180 |
0 -120 |
0 +20 |
0 0 |
0 -50 |
0 -390 |
0 -1,2 |
||
Ниж-ний пояс |
r-2 r-5 |
+90 +120 |
+110 +140 |
+70 +160 |
+30 +20 |
+60 +80 |
0 0 |
+290 +380 |
+1,3 +1,6 |
||
Стой-ки |
а-1 3-4 |
-20 -40 |
-55 -110 |
-55 -110 |
0 +10 |
0 0 |
0 0 |
-77 -150 |
0 0 |
||
Раско-сы |
1-2 2-3 |
-180 +90 |
-200 +110 |
-140 +90 |
+50 -30 |
0 +50 |
-60 -50 |
-420 +250 |
-1,5 +1,2 |
||
Шпрен-гели |
|
|
|
|
|
|
|
|
|
||
В таблице, в качестве примера, приведены значения нагрузок для различных стержней фермы (рис.8). Для определения расчетного усилия стержня необходимо выбрать наиболее неблагоприятное для него сочетание нагрузок. Например, для стержня с-3 таким сочетанием является сумма усилий 3,4 и 8 колонок, для стержня r-5 это сумма усилий 3.5.6 и 7 колонок, а для стержня 2-3 сумма усилий 3,4 и 7 колонок.
