Угол между прямыми. Угол между прямой и плоскостью.
Угол между прямыми в пространстве равен
углу между их направляющими векторами.
Поэтому, если две прямые заданы
каноническими уравнениями вида
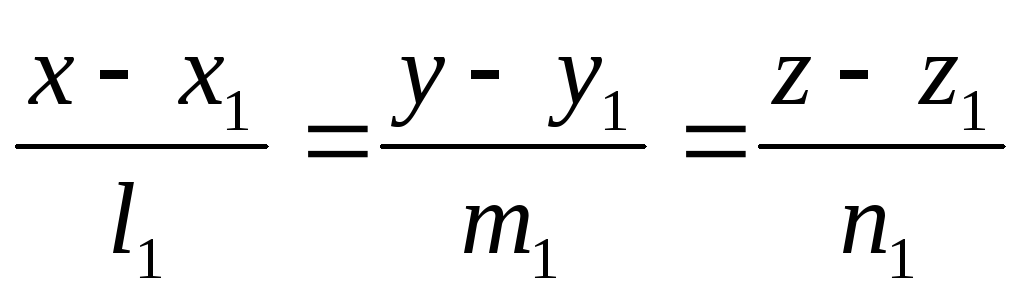 и
и
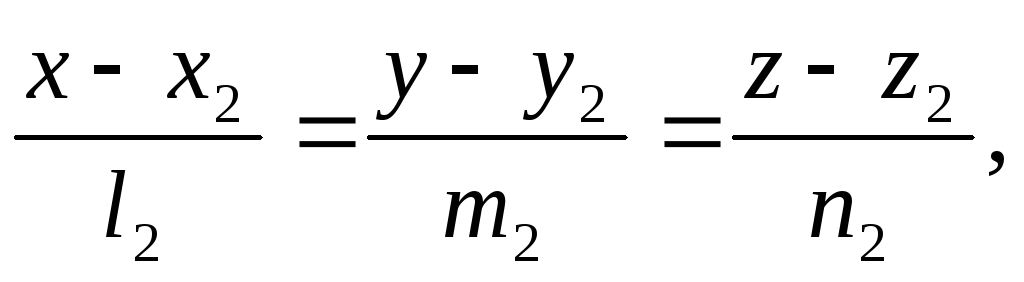 косинус угла между ними можно найти по
формуле:
косинус угла между ними можно найти по
формуле:
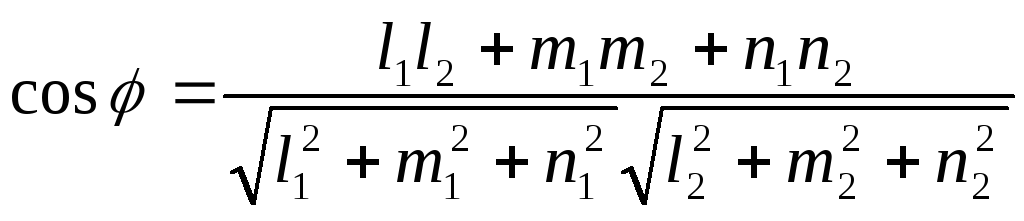 . (8.14)
. (8.14)
Условия параллельности и перпендикулярности
прямых тоже сводятся к соответствующим
условиям для их направляющих векторов:
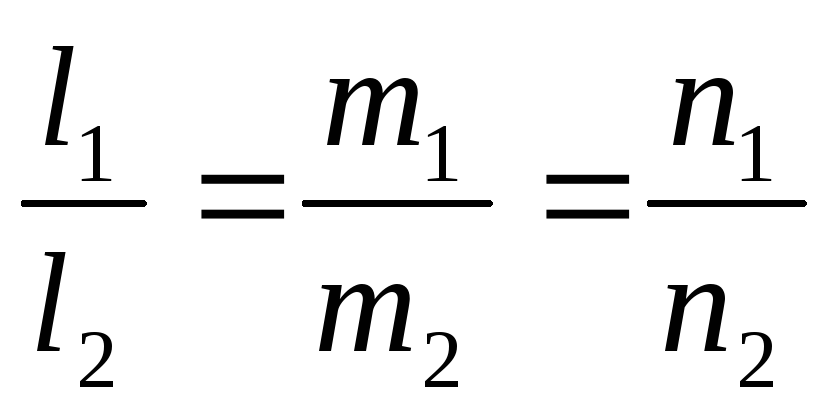 - условие параллельности прямых,
(8.15)
- условие параллельности прямых,
(8.15)
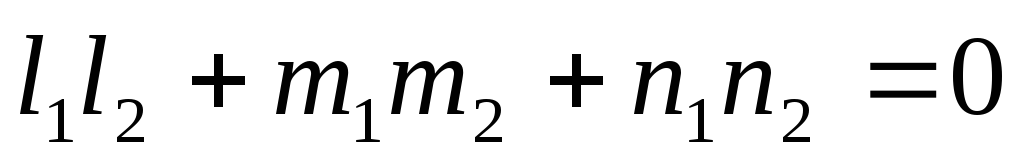 - условие перпендикулярности прямых.
(8.16)
- условие перпендикулярности прямых.
(8.16)
Угол φ между прямой, заданной
каноническими уравнениями
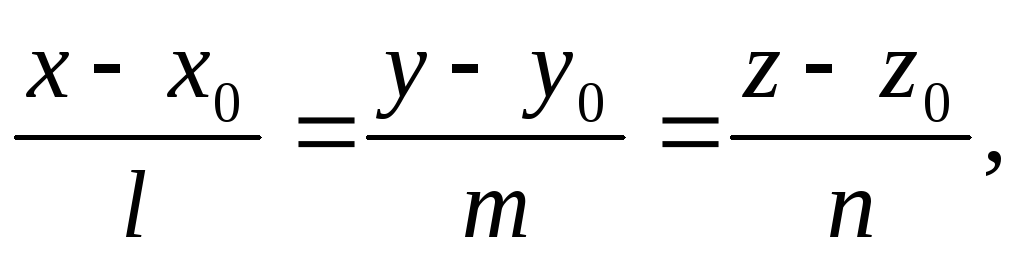 и
плоскостью, определяемой общим уравнением
и
плоскостью, определяемой общим уравнением
Ax +
By + Cz
+ D = 0,
можно рассматривать
как дополнительный к углу ψ между
направляющим вектором прямой и нормалью
к плоскости. Тогда
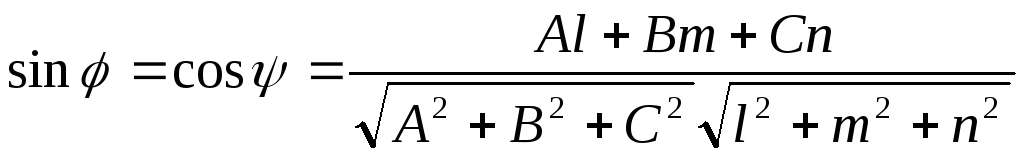 (8.17)
(8.17)
Условием параллельности прямой и
плоскости является при этом условие
перпендикулярности векторов n
и а:
Al + Bm
+ Cn = 0,
(8.18)
а условием перпендикулярности прямой
и плоскости – условие параллельности
этих векторов: A/l
= B/m
= C/n.
(8.19)

