
- •Квадратичные формы
- •Элементы теории множеств
- •3. Аксиома сложения и умножения.
- •4. Аксиомы порядка.
- •5. Аксиомы порядка, связанные с операциями.
- •6. Аксиома непрерывности.
- •Функции действительных переменных
- •Способы задания функции одной переменной
- •Функции на множестве натуральных чисел в комбинаторике
- •Последовательности
- •Предел числовой последовательности
- •Предел функции. Свойства пределов
- •Бесконечно малые и бесконечно большие функции
- •Свойства пределов функций
- •Второй замечательный предел и его следствия
Квадратичные формы
Квадратичной
формой в пространстве
![]() с
координатами
с
координатами![]() является выражение вида
является выражение вида![]() ,
где
,
где![]() ,
– произвольные числа. Квадратичной
формой в пространстве
,
– произвольные числа. Квадратичной
формой в пространстве![]() с
координатами
с
координатами![]() является выражение вида
является выражение вида![]() .
Квадратичной формой в пространстве
.
Квадратичной формой в пространстве![]() является выражение вида
является выражение вида
 ,
где матрица
,
где матрица
![]() симметрична относительно главной
диагонали.
симметрична относительно главной
диагонали.
Часто возникает
вопрос, при каких коэффициентах
квадратичная форма будет сохранять
знак при произвольных значениях
переменных
![]() .
.
Из свойств квадратных
трехчленов
![]() следует,
что квадратичная форма
следует,
что квадратичная форма![]() положительна
тогда и только тогда, когда для
коэффициентов квадратичной формы
справедливы условия: 1)
положительна
тогда и только тогда, когда для
коэффициентов квадратичной формы
справедливы условия: 1)![]() ,
2)
,
2)![]() (или
(или![]() ).
Она отрицательна, если
).
Она отрицательна, если
1)
![]() ,
2)
,
2)![]() (или
(или![]() ).
).
Для квадратичной
формы высших порядков рассматривают
последовательность определителей
 из коэффициентов матрицы
из коэффициентов матрицы![]() ,
расположенных в левом верхнем углу.
Если
,
расположенных в левом верхнем углу.
Если![]() ,
то квадратичная форма положительна.
Если
,
то квадратичная форма положительна.
Если![]() (определители с нечетными номерами
отрицательны, определители с четными
номерами положительны), то квадратичная
форма отрицательна.
(определители с нечетными номерами
отрицательны, определители с четными
номерами положительны), то квадратичная
форма отрицательна.
Элементы теории множеств
Понятие множества
или совокупности
принадлежит к числу простейших
математических понятий. Оно не имеет
точного определения. Любое множество
задается своими элементами. Примерами
являются множество книг в библиотеке
или множество студентов, присутствующих
на занятии. Обычно множество обозначают
заглавными латинскими буквами (A),
а его элементы строчными латинскими
буквами (a).
То, что элемент принадлежит множеству,
обозначают так: a![]() A.
Если a
не принадлежит A,
то этот факт обозначают так: a
A.
Если a
не принадлежит A,
то этот факт обозначают так: a![]() A.
A.
Чтобы задать множество, следует или перечислить его элементы, или указать характеристическое свойство его элементов, то есть такое свойство, которым обладают все элементы множества и только они. Мы уже знакомы со следующими примерами подмножеств вещественных чисел.
Примеры. 1. Множество натуральных чисел: N={1, 2, 3,…,n, n+1,…}. Из записи следует, что все натуральные числа, начиная с двойки, получаются прибавлением единицы к предыдущему числу.
Множество целых чисел: Z={0, 1 ,–1, 2, –2,…,n, –n,…}.
Множество рациональных чисел:
 ={
={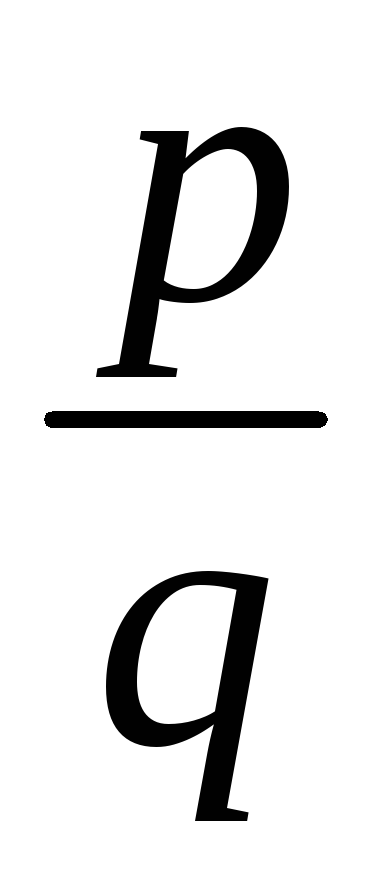 |
| }.
}.Множество всех действительных (вещественных) чисел R.
Два множества
равны тогда и только тогда, когда состоят
из одних и тех же элементов. Если все
элементы множества A
содержатся в множестве B,
то говорят, что A
является подмножеством множества B
и обозначают A![]() B.
Поэтому
B.
Поэтому
![]() означает, что
означает, что![]() и одновременно
и одновременно![]() .
.
Очевидно, что
![]() .
.
В рамках
рассматриваемой математической теории
вводят два исключительных множества:
пустое множество (![]() ),
не содержащее элементов, и универсальное
множество или «универсум» (U),
содержащее все элементы данной теории.
),
не содержащее элементов, и универсальное
множество или «универсум» (U),
содержащее все элементы данной теории.
Аксиоматика операций над множествами.
Основными операциями над множествами являются следующие.
1.
Дополнение. Для
любого множества
![]() определим дополнение
определим дополнение![]() .
.
Например, в множестве
вещественных чисел дополнением к
множеству
![]() является множество всех иррациональных
чисел.
является множество всех иррациональных
чисел.
2. Объединение.
Для любых
двух множеств
![]() определим объединение
определим объединение![]() .
.
Например, объединением отрезков [1,3] и [2,7] является отрезок [1,7].
Пересечение. Для любых двух множеств
 определим пересечение
определим пересечение .
.
Например, пересечением отрезков [1,3] и [2,7] является отрезок [2,3].
Для иллюстрации операций над множествами вводят диаграммы Эйлера-Венна – круги, обозначающие множества. Так, введенные нами операции иллюстрируются следующим образом.

А
![]()
![]()
Подчеркнем, что диаграммы Эйлера-Венна не могут служить доказательствами равенства множеств.
Кроме введенных
нами трех операций над множествами
существуют еще операции, которые могут
быть представлены как комбинация
простейших операций. Введем операцию
вычитания
множеств:
![]() .
На диаграмме Эйлера-Венна результат
вычитания выглядит так:
.
На диаграмме Эйлера-Венна результат
вычитания выглядит так:

А\В
![]() =
U\В
=
U\В
Можно доказать,
что
![]() .
Для доказательства равенства двух
множеств следует убедиться в том, что
все элементы первого множества принадлежат
второму и все элементы второго множества
принадлежат первому.
.
Для доказательства равенства двух
множеств следует убедиться в том, что
все элементы первого множества принадлежат
второму и все элементы второго множества
принадлежат первому.
Помимо введенных
операций над множествами рассматривают
декартово
произведение
двух множеств. Декартовым произведением
множеств A
и B
называется множество
![]() ,
элементы которого задаются двумя
координатами, из которых первая –
элемент множестваA,
а вторая – элемент множества B.
,
элементы которого задаются двумя
координатами, из которых первая –
элемент множестваA,
а вторая – элемент множества B.
Например, если A
– множество
названий всех улиц какого-то города, B
– множество
номеров домов от 1-го до 10-го, то
![]() – множество адресов городских домов,
расположенных в начале улиц. В данном
случае количество этих адресов равно
произведению количеству городских улиц
на 10.
– множество адресов городских домов,
расположенных в начале улиц. В данном
случае количество этих адресов равно
произведению количеству городских улиц
на 10.
Множество точек
плоскости обозначается
![]() .
.
Аксиоматика действительных чисел
Аксиомы сложения.
1)
![]() справедливо
справедливо
![]() .
.
2)
![]() справедливо
справедливо
![]() .
.
3)
![]() (нейтральный
элемент сложения) такой, что
(нейтральный
элемент сложения) такой, что
![]() справедливо
справедливо
![]() .
.
4)
![]() такой, что
такой, что
![]() .
.
Аксиомы умножения.
1)
![]() справедливо
справедливо
![]() .
.
2)
![]() справедливо
справедливо
![]() .
.
3)
![]() (нейтральный
элемент умножения) такой, что
(нейтральный
элемент умножения) такой, что
![]() справедливо
справедливо
![]() .
.
4)
![]() такой, что
такой, что
![]() .
.
