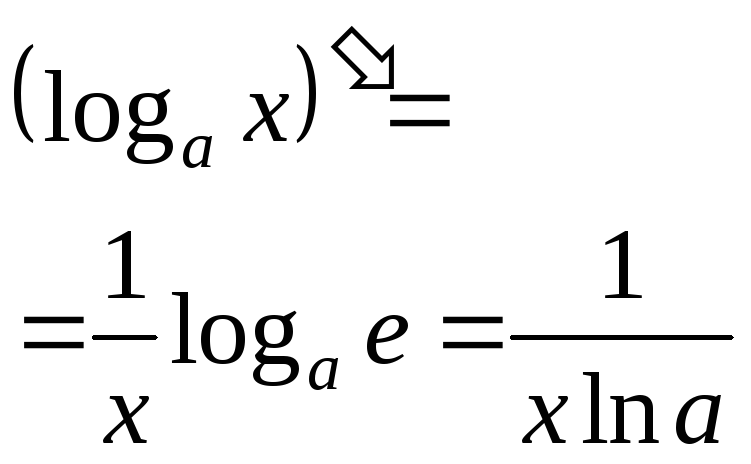lekts_matem7_8

10

Непрерывность функции

Определение 1. Функция непрерывна в точке , если предел этой функции при равен значению функции в предельной точке, то есть .

Применяя второе определение предела функции в точке, получим

Определение 2. Функция непрерывна в точке , если .

Определение 3. Функция непрерывна в точке , если , где приращение аргумента функции (), а – приращение функции, соответствующее приращению ее аргумента .

Доказательство следует из первого определения непрерывной функции

Здесь первый из пределов вычисляется с помощью определения 1, второй – как предел постоянной, поскольку не зависит от .

Определение 4. Функция непрерывна в точке , если

.

Определение 5. Функция непрерывна в некоторой области, если она непрерывна во всех точках этой области.

Все степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические функции непрерывны в областях существования.

Свойства непрерывных функций

Сумма непрерывных функций – есть непрерывная функция.

Действительно, из определения 1 непрерывности следует, что если и , то

.

2). Произведение непрерывных функций есть функция непрерывная.

3). Частное непрерывных функций – функция непрерывная, если знаменатель в предельной точке не равен нулю.

Доказательства второго и третьего свойств также следует из свойств пределов.

4). Пусть функция непрерывна в точке , пусть функция непрерывна в точке . Тогда функция непрерывна в точке .

Очевидно, что

.

Так как согласно определению 3 непрерывности при и при , получим: при .

Таким образом, непрерывная функция от непрерывной функции есть функция непрерывная.

Пример. Функция непрерывна во всех точках числовой оси, так как функция непрерывна на , а функция непрерывна на множестве неотрицательных чисел.

Точки разрыва функции

Определение. Точкой разрыва функции называется внутренняя точка области задания функции, в которой нарушается непрерывность функции. Если в точке разрыва функция, к тому же, не существует, ее часто называют особой точкой. Так функция существует на всей числовой оси, кроме точки . Эта точка – особая, и в ней функция терпит разрыв.

Разрыв может быть конечным, если и принимают конечные, но не равные значения. Разность между этими значениями называют скачком функции в точке разрыва.

Пример. Функция 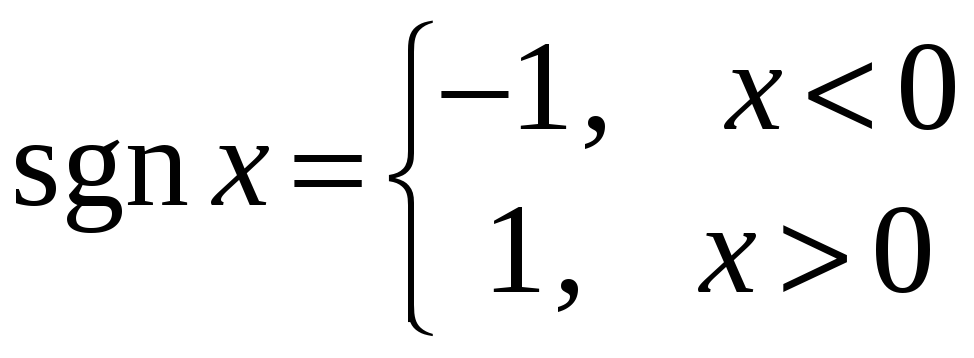. Очевидно, ,

.

Разрыв бесконечный, если левый, правый или оба предела бесконечны.

Пример. 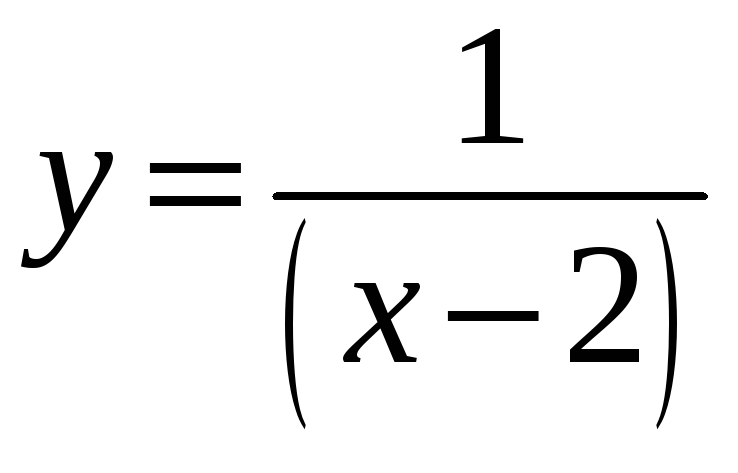. Имеем , .

Разрыв называется устранимым, если и эти пределы конечны, но функция в точке не задана.

Пример. Функция не может быть задана при (деление на ноль), однако и левый и правый ее пределы равны 1, что следует из первого замечательного предела.

Устранить этот недостаток можно введением другой функц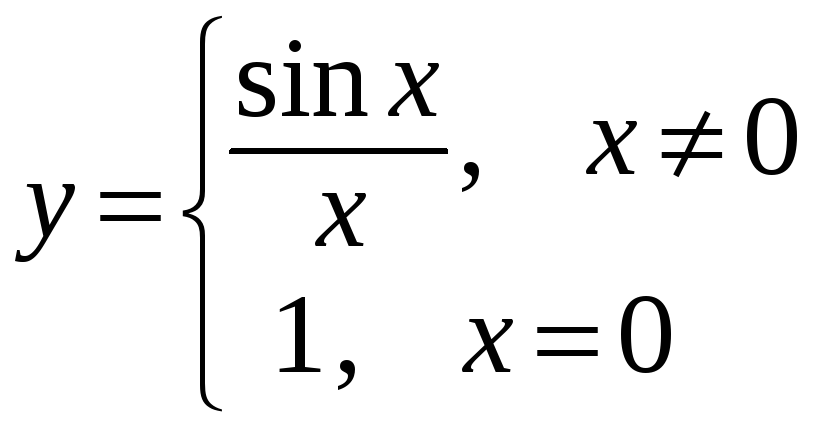ии . Эта функция совпадает с заданной во всех точках, кроме 0, но она существует и непрерывна на всей числовой оси, что следует из свойств непрерывной функции.

Вычисление пределов

Вначале выясним, в чем смысл вычисления пределов? В точках, где функция определена и непрерывна, соответствующий предел можно получить, вычислив ее значение. Особый подход к вычислению предела необходим, когда желательно знать поведение функции в окрестности особой точки, или установить, как ведет себя функция при стремлении ее аргумента к бесконечности.

Рассмотрим функци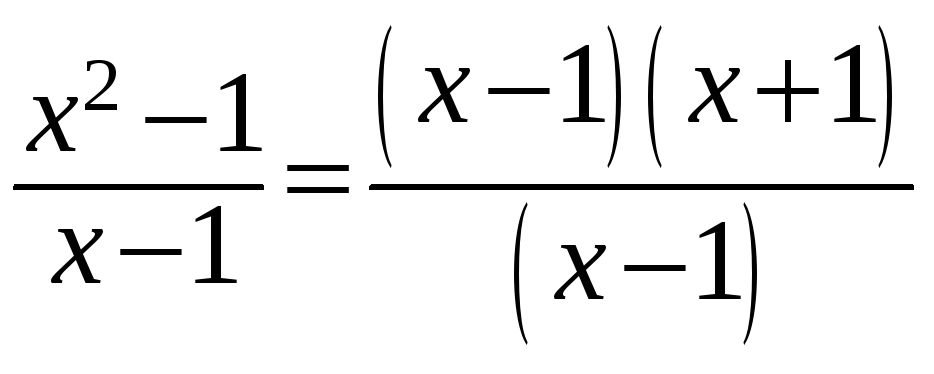и и _. Последняя получена в результате формального сокращения числителя и знаменателя первой на множитель . Это разные функции, так как имеют разные области существования, хотя их значения совпадают повсюду, кроме точки . В этой точке первая функция не существует (деление на ноль), вторая равна 2. Теперь вычислим предел . Рассмотрим последовательность действий 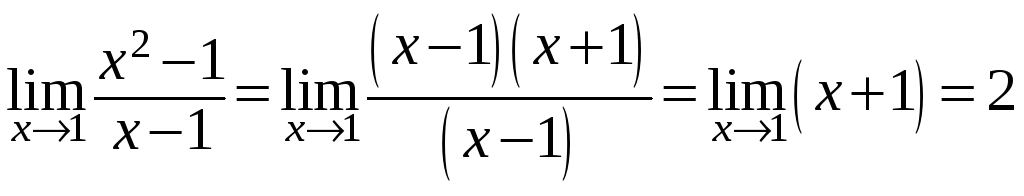под знаком предела. Здесь мы заменяем одну функцию на другую в той области, где они совпадают, ибо при вычислении предела стремится к предельной точке 1, не попадая в саму эту точку. Итак, рассматриваемая функция в точке 1 не существует, но стремится к значению 2 при . Исследуем . Он равен 3, так как и являются бесконечно малыми при . Сокращение на также законно, поскольку , а только стремится к бесконечности, то есть принимает сколь угодно большие, но конечные значения.

Правила вычисления предела

Чтобы вычислить , необходимо.

1. Попробовать подставить в функцию, стоящую под знаком предела, . Если функция в этой точке непрерывна, в соответствии формулой 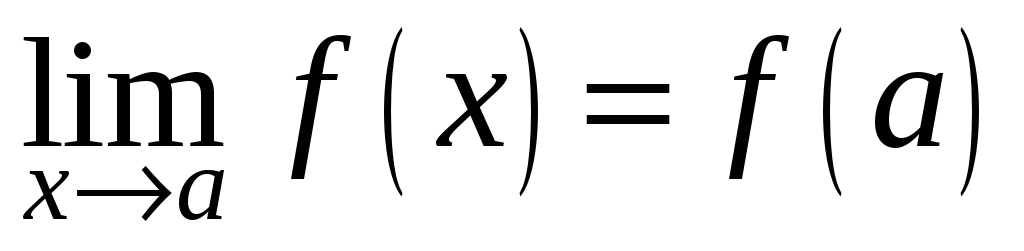предел равен числу .

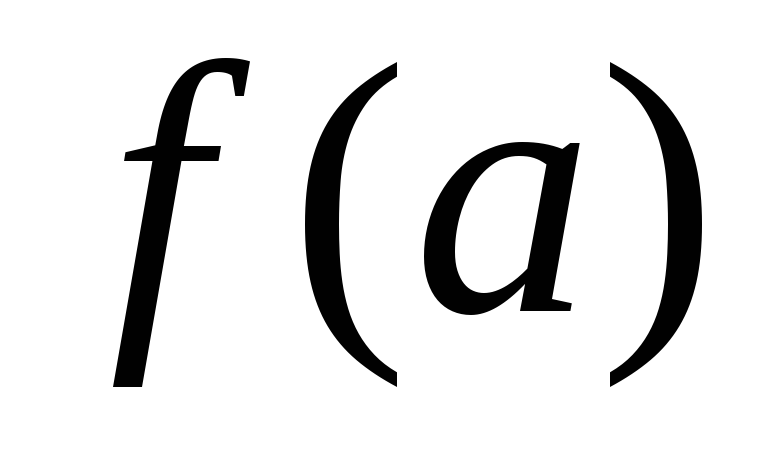2. Если точка не входит в область определения функции, то конечный предел может не существовать, и если абсолютная величина функции неограниченно увеличивается при стремлении переменной к , то пределом является бесконечность.

3. Если в результате подстановки получается неопределенность, то есть выражение вида 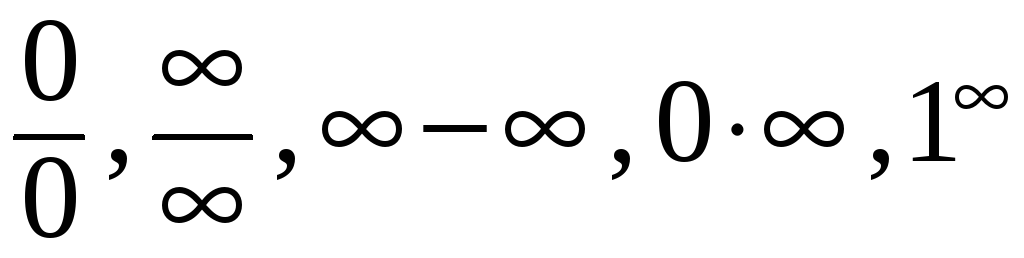, следует раскрыть эту неопределенность, сделав сокращения, или привести получаемое выражение к замечательному пределу или его следствию. Примеры.

1. .

2. .

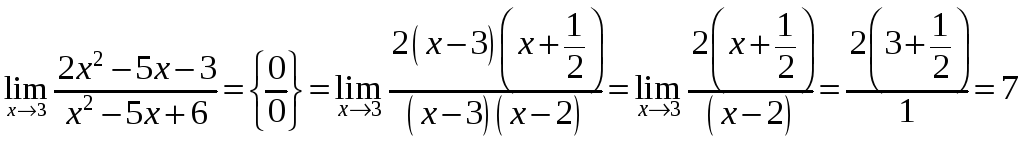Неопределенности показывает, что в числителе и знаменателе присутствуют бесконечно большие функции. Чтобы избавиться от них следует вынести самую большую величину в числителе и знаменателе за скобки, произвести сокращение, после чего еще раз применить пункт 1 правил.

Примеры.

1. .

2. .

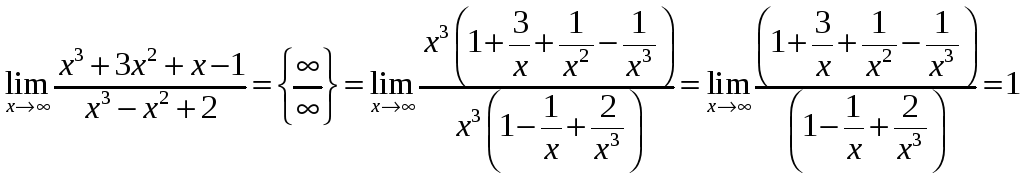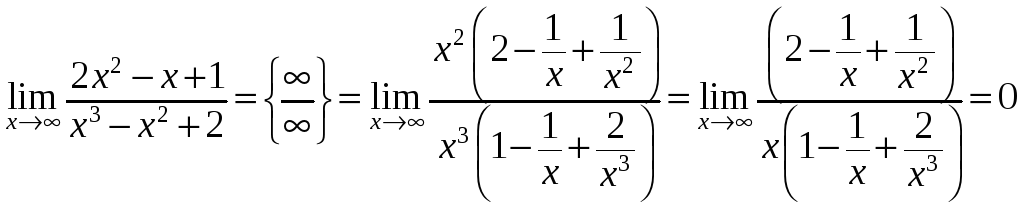3. Неопределенности приводятся вначале к виду 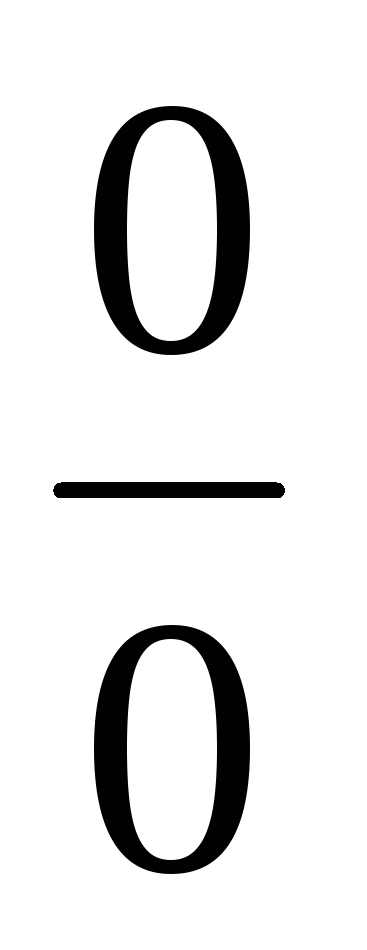или , затем раскрываются одним из перечисленных выше способов.

Примеры.

1. 

2. .

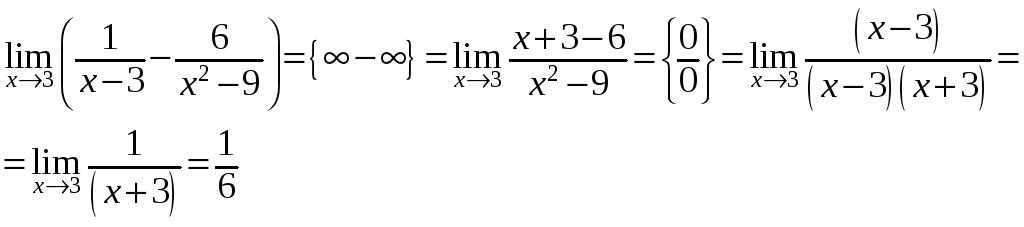
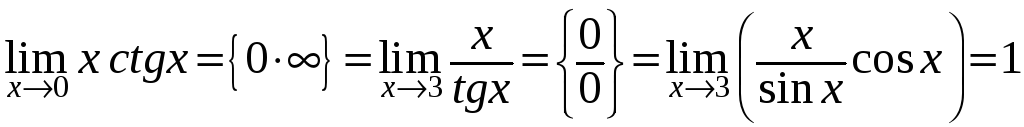3. Проверить непрерывность функции .

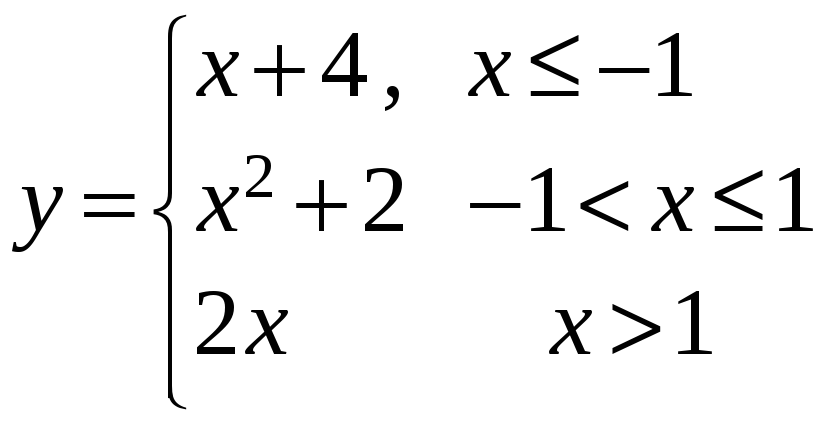4. Поскольку функци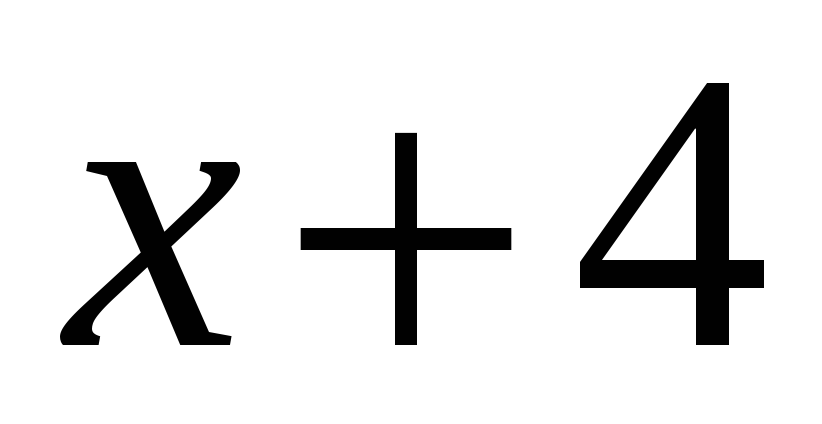и , и 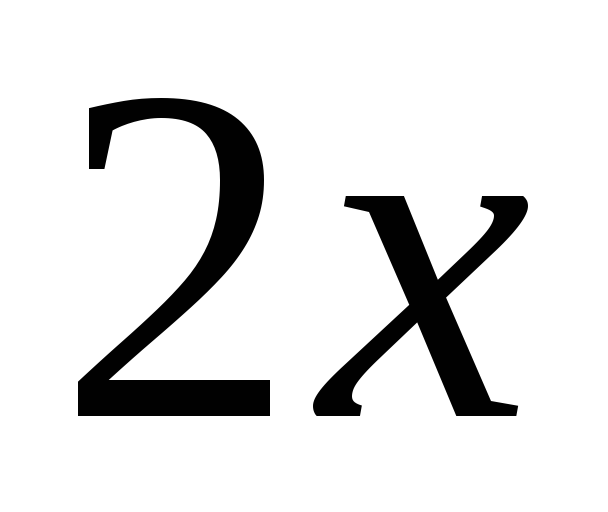непрерывны в областях их задания, достаточно рассмотреть функцию в точках стыковки этих функций. Итак, для 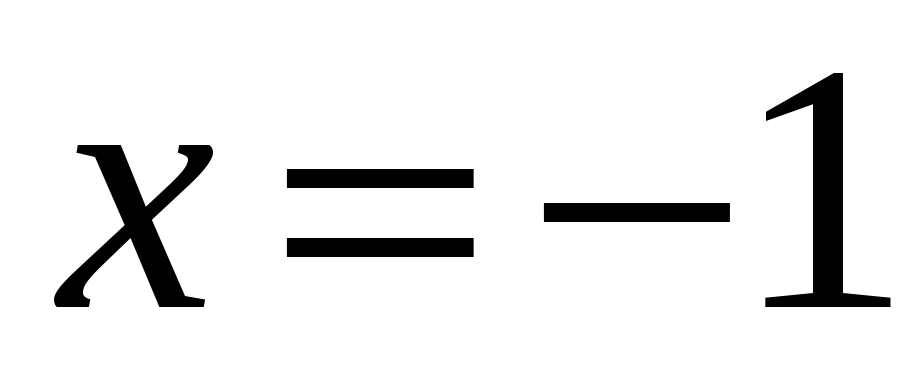имеем , , .

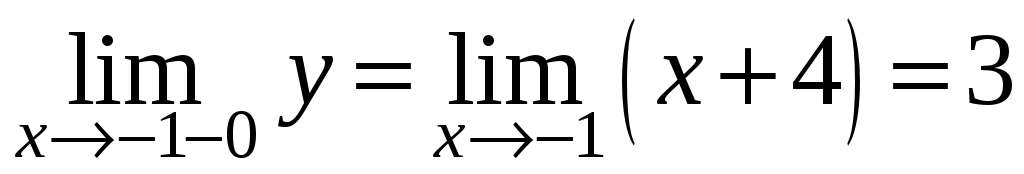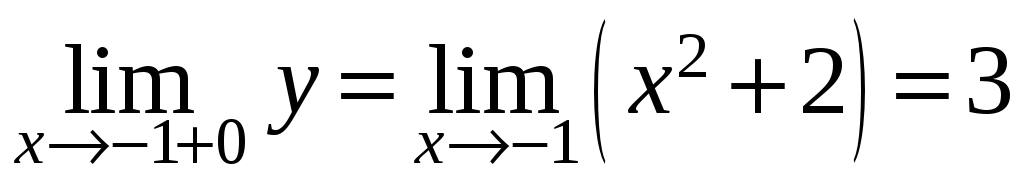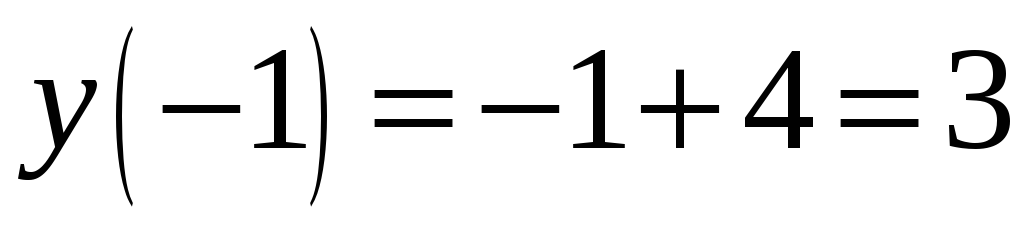Функция в этой точке непрерывна согласно определению 4.

Для имеем , , . Условие непрерывности в точке не выполняется.

Следовательно, функция непрерывна на всей числовой оси за исключением точки , где она имеет конечный разрыв со скачком

(-1).

Производная. Дифференциал функции

Задача о проведении касательной к кривой

Пусть заданная кривая является графиком непрерывной функции , и требуется провести касательную к этой кривой в точке . Заметим, что касательная – это прямая, получающаяся в пределе из хорд, проходящих через точки и , когда . Уравнение хорды – прямой, проходящей через две заданные различные точки, – имеет вид: или . Делая предельный переход при , получим предельное значение углового коэффициента хорд – угловой коэффициент касательной: . На рисунке касательная представлена пунктиром. Итак, , где – угол, образованный касательной с положительным направлением оси

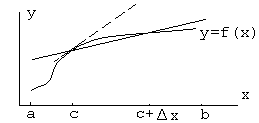
Очевидно, что существуют непрерывные кривые, в некоторых точках которых провести касательную невозможно.

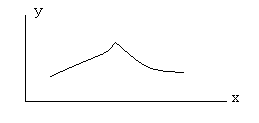
Возникает вопрос: какое условие нужно наложить на функцию в окрестности точки , чтобы в соответствующей точке можно было провести касательную к графику этой функции.

Определение 1. Функция называется дифференцируемой в точке , если ее приращение представимо в виде , причем – константа, – бесконечно малая функция, более высокого порядка малости, чем , то есть .

Установим значение , для чего вычислим

.

Назовем число производной функции в точке и обозначим ее , в результате получаем определение производной и, кроме того,

.

Как было сказано выше, второе слагаемое в выражении приращения функции – величина более высокого порядка малости, чем величина , а следовательно, и чем величина . Другими словами, первое слагаемое в выражении приращения функции представляет основную часть приращения функции. Называют его дифференциалом функции в точке и обозначают В целях единообразия и для того, чтобы подчеркнуть, что – бесконечно малая величина, приращение аргумента в этой формуле обозначают . Тогда , откуда следует второе обозначение производной . Связь между приращением функции и ее дифференциалом изображена на рисунке 1.

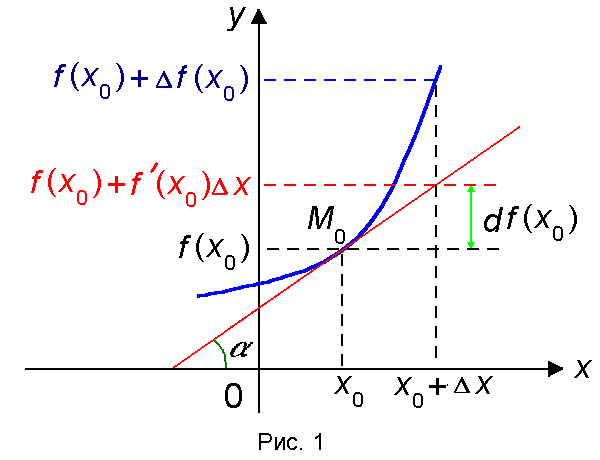
Замечание. Геометрическим смыслом производной является тангенс угла наклона касательной к кривой в точке . Поэтому уравнение касательной к кривой в точке имеет вид .

Физическим смыслом производной является скорость в момент , когда зависимость длины пути от скорости задается функцией .

Правила дифференцирования

1. Производная суммы функций есть сумма производных этих функций.

Пусть , тогда

.

Очевидно, .

2. .

3. .

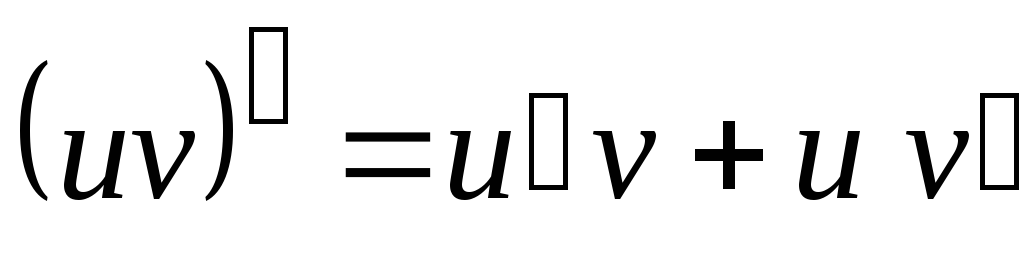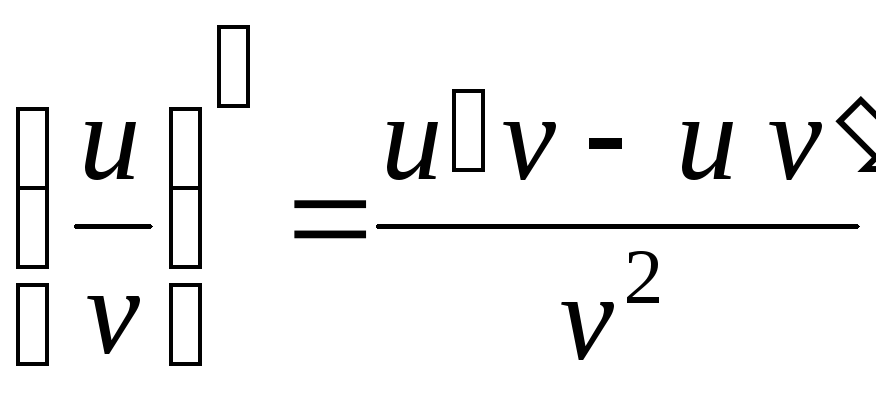Свойства 2) и 3) доказываются аналогично свойству 1).

4) Пусть функция дифференцируема в точке , . Пусть функция дифференцируема в точке . Тогда сложная функция дифференцируема в точке , причем .

Действительно,

.

Производная обратной функции

Даны функция и обратная ей функция , т.е. . Если дифференцируема в точке и ,тогда дифференцируема в точке , при этом .

Действительно, если , то . Теперь

.

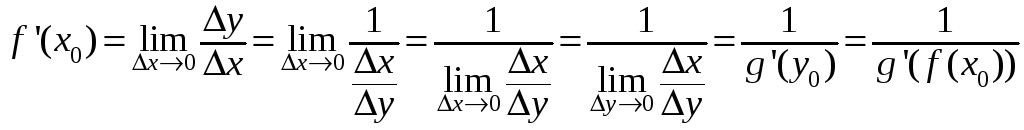Следовательно,

Производная параметрически заданной функции Пусть 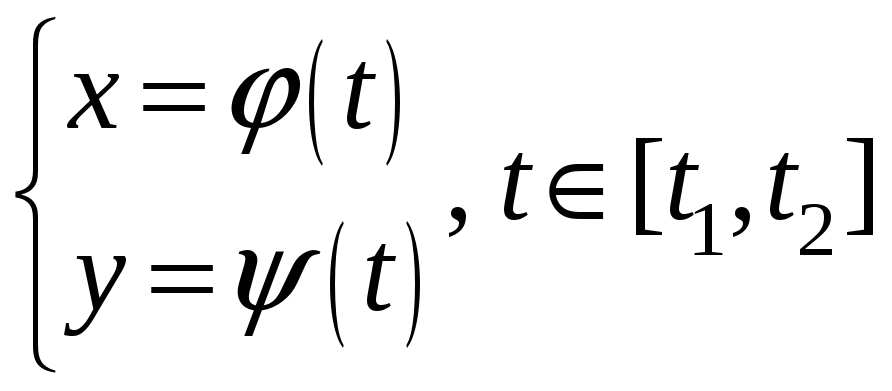, причем функции Обе функции и дифференцируемы в точке . Вычислим в точке .

.

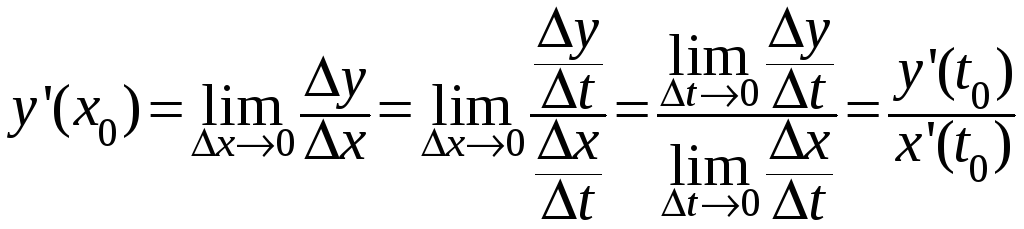Итак, .

Таблица производных

, если постоянная

Докажем некоторые из этих формул.

1. Если , то , и первая формула доказана.

2. Пусть , тогда

.

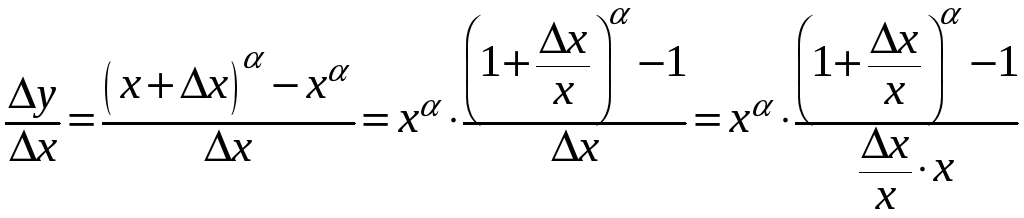Переходя к пределу при и используя 3-е следствие из второго замечательного предела, получим вторую формулу.

3. Пусть , тогда .

Используя первый замечательный предел, получим

.

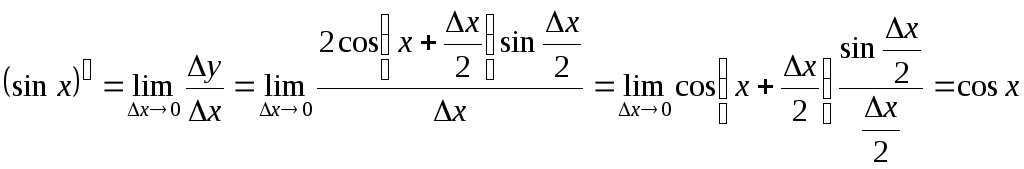4. Пусть, тогда

5. Пусть , тогда

, теперь применяя

первое следствие из второго замечательного предела, получим

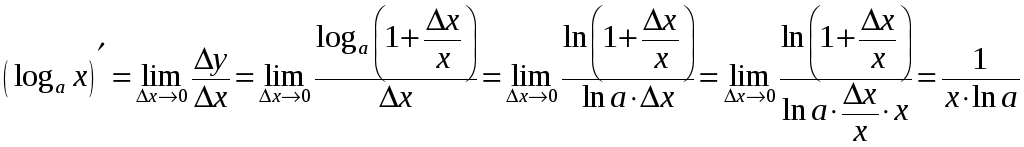
6. Пусть , тогда, , , значит

   .

7. Пусть , тогда ,  .

.

Примеры вычисления производных

1. 

,

2. ,

3. ,

.

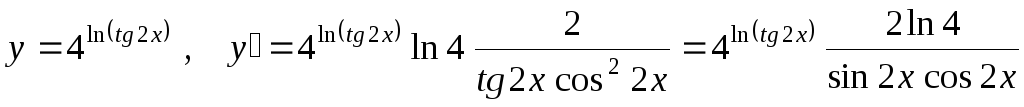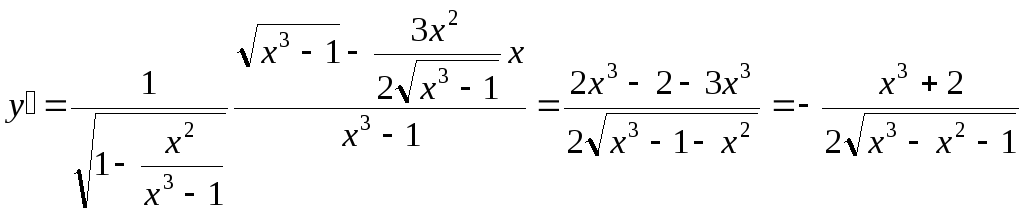Дифференцирование неявно заданных функций

Если функция задана неявно, перед дифференцированием следует определиться, какую переменную считать аргументом. Пусть . Считаем назависимой переменной, функцией. Можно из уравнения определить и , тогда и . Но можно поступить по-другому. Дифференцируем обе части уравнения по переменной , используя при этом правило дифференцирования сложных функций , откуда следует .