Длина дуги кривой

Декартова система координат

Явное задание функции

На отрезке задана кривая. Определить длину дуги этой кривой.

Разобьем отрезок точкаминаэлементарных отрезков. Восстановим перпендикуляры из точек разбиения отрезка до пересечения с кривой, пусть. Соединим точки пересечения перпендикуляров к кривой хордами, в результате получаем ломаную линию, длина которой приближенно дает длину дуги кривой. На рисунке 9показано, как получается ломаная линия в случае.

Из точек пересечения каждого из указанных выше перпендикуляров с кривой проведем отрезки прямых, параллельных оси абсцисс, до пересечения с соседним перпендикуляром, в итоге получаем прямоугольных треугольников. На рисунке 9изображенй треугольник, его катеты равныи. Из теоремы Пифагора следует, что длина гипотенузы равна. Очевидно, длина всей ломаной, причем с ростом числа разбиенийдлина ломаной все менее отличается от длины кривой. При, когда все, получаем точное значение длины дуги кривой. Итак,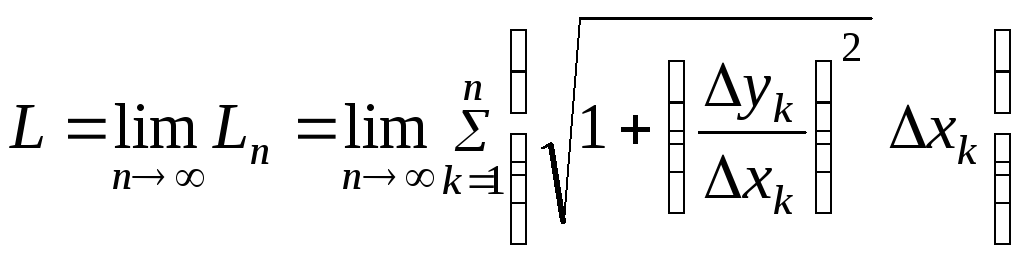. Таким образом, длина дугипредставляет собой предел интегральной суммы, то есть определенный интеграл. Поскольку,.

Получена формула длины дуги кривой на отрезке .

Пример 1. Найти длину верхней части дуги параболына отрезке. Очевидно,, следовательно,

.

Получен интеграл от дробно рациональной функции, которая представляется в виде суммы простейших дробей

.

Приведем дроби в правой части тождества к общему знаменателю, совпадающей со знаменателем дроби в левой части и приравняем после этого числители дробей

,

раскроем некоторые скобки

.

Приравнивая коэффициенты при одинаковых степенях в обеих частях тождества, приходим к системе уравнений

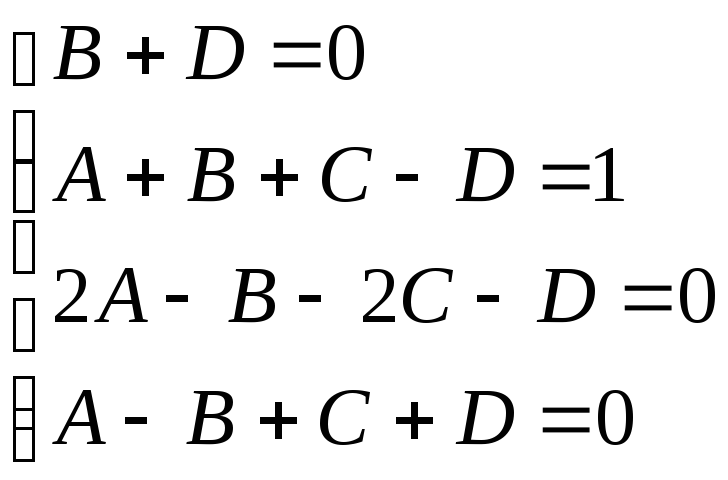
Из первого уравнения имеем , из третьего с учетом первого, из четвертого, из второго, откуда,.

Итак,

.

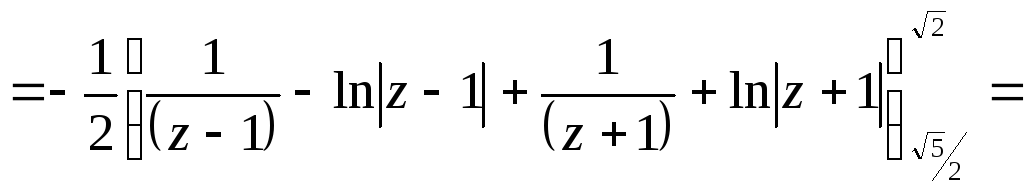
Итак,

.

Получим тот же результат с помощью МАКСИМЫ

Результаты совпадают, поскольку

.

Пример 2. Вычислить длину дуги кривой в области.

Поскольку ,

.

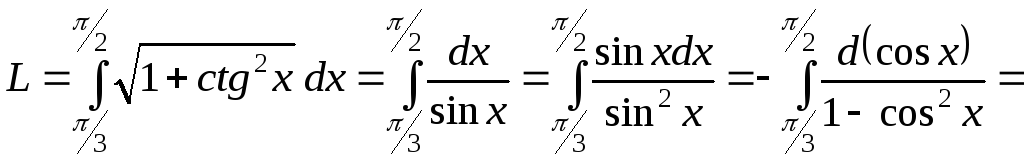
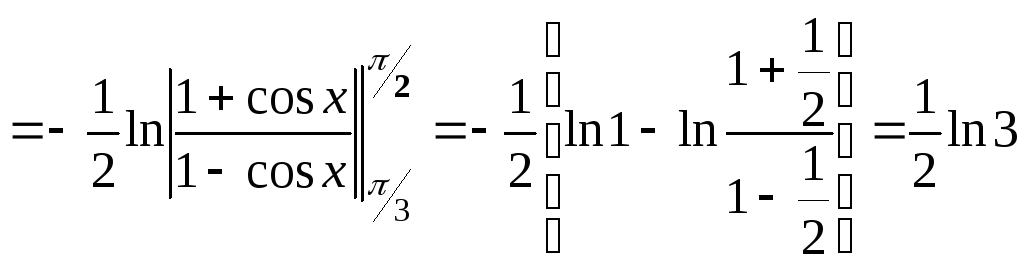Параметрическое задание функции

Чтобы получить формулу длины дуги кривой на отрезке, когда ее уравнение задано параметрически , следует в формулепроизвести замену переменной

,

откуда имеем

.

Здесь значения переменной, соответствующиеи.

Пример 1. Вычислить длину дуги одной арки циклоиды .

Как говорилось выше, одна арка циклоиды расположена в области . Тогда

.

Пример 2. Вычислить длину дуги кривой 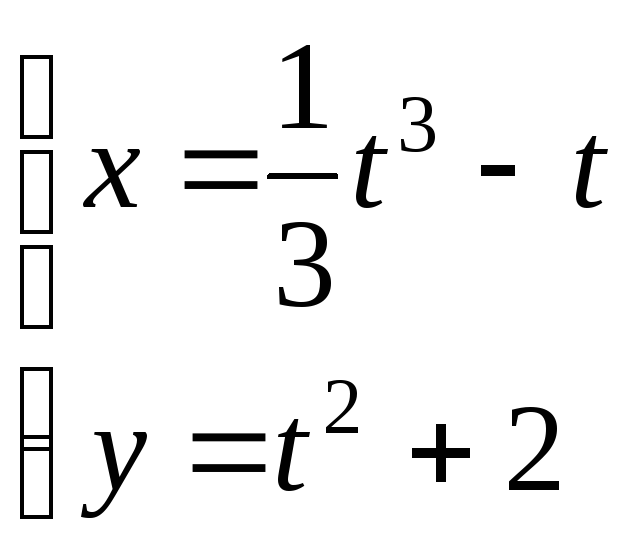отдо.

.

Полярная система координат

Рассмотрим кривую, заданную в полярной системе координат . Определим длину дуги этой кривой в области.

Перейдем к полярной системе координат, воспользовавшись формулами . Считая теперь, что уравнение линии задано в параметрическом виде, гдепараметр, используем формулу длины дуги для параметрически заданной функции

,

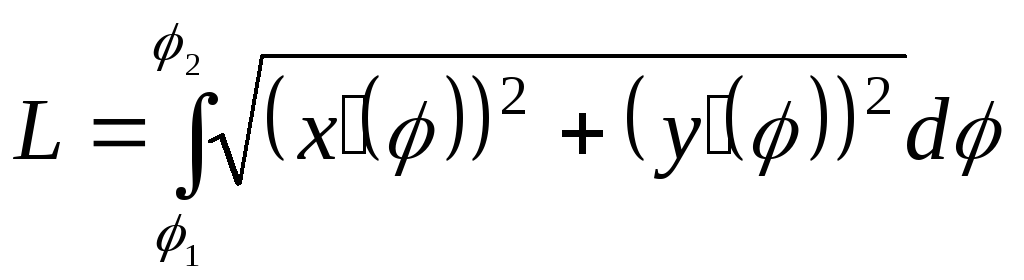для чего определим производные

,

откуда следует

,

в самом деле

.

Тогда в полярной системе координат длина дуги определяется формулой

.

Пример 1. Вычислить длину кардиоиды . Рисунок кардиоиды приведен ранее, из него видно, что интегрирование должно происходить в области. Итак,

.

Пример 2. Вычислить длину дуги линии в области.

.

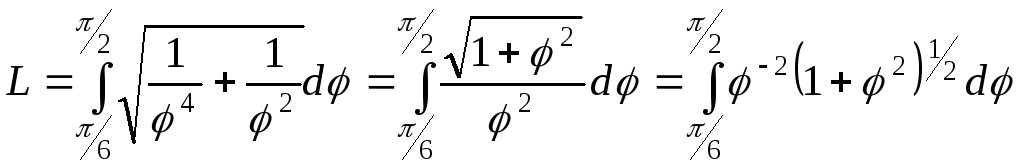Интеграл от дифференциального бинома вычисляем подстановкой

.

Тогда

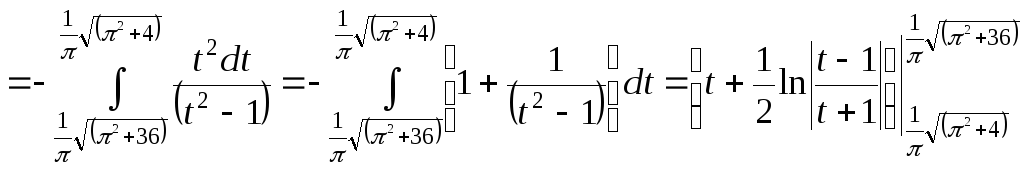
В итоге

.
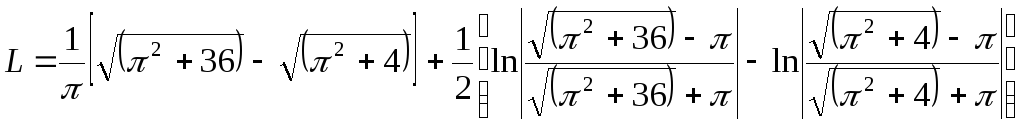