Решение

Вариант 1

1. Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях — четная, причем на грани хотя одной из костей появится шестерка.

Решение:

Возможные элементарные исходы обозначим упорядоченной парой чисел, выпавших на первом и втором кубиках соответственно. Всего получится 36 пар.

(1;1)	(2;1)	(3;1)	(4;1)	(5;1)	(6;1)
(1;2)	(2;2)	(3;2)	(4;2)	(5;2)	(6;2)
(1;3)	(2;3)	(3;3)	(4;3)	(5;3)	(6;3)
(1;4)	(2;4)	(3;4)	(4;4)	(5;4)	(6;4)
(1;5)	(2;5)	(3;5)	(4;5)	(5;5)	(6;5)
(1;6)	(2;6)	(3;6)	(4;6)	(5;6)	(6;6)

Благоприятствующими интересующему нас событию (хотя бы на одной грани появится шестерка, сумма выпавших очков - четная) являются следующие пять исходов (2;6), (4;6), (6;6), (6;4), (6;2).

Ответ:

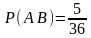
2. Брошены две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна семи; б) сумма выпавших очков равна восьми, а разность — четырем; в) сумма выпавших очков равна восьми, если известно, что их разность равна четырем; г) сумма выпавших очков равна пяти, а произведение — четырем.

Общее число возможных элементарных исходов испытания равно

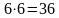
а) среди общего количества элементарных исходов событию благоприятствуют только 6: (1;6), (6;1), (2;5), (5;2), (3;4), (4;3). Вероятность составит:

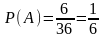
б) среди общего количества элементарных исходов событию благоприятствуют только 2: (2;6), (6;2). Вероятность составит:

в) Пусть событие A состоит в том, что сумма выпавших очков равна восьми, событие B – разность очков равна четырем. Воспользуемся формулой нахождения условной вероятности: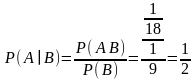

г) среди общего количества элементарных исходов событию благоприятствуют только 2: (1;4), (4;1). Вероятность составит:

3. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.

Решение:

Событие А – все три выбранные детали окрашены. Общее число исходов – это число всевозможных наборов по 3 элемента, которые можно составить из множества, состоящего из 15 элементов, не учитывая порядок равно (сочетаний):

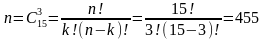
Число исходов испытания, благоприятствующих событию А, равно числу всевозможных наборов по 3 детали, которые можно составить из множества окрашенных деталей, то есть:

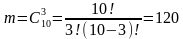
Вероятность события А равна отношению числа исходов, благоприятных событию А к числу всех элементарных исходов.

Ответ:

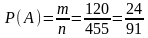
4. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

Решение:

Первую цифру можно набрать 10 способами, вторую – 9, так как одна цифра уже использована и третью – 8. Тогда общее число возможных размещений равно:

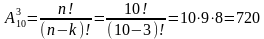
Искомая вероятность равна отношению числа исходов, благоприятных событию А к числу всех элементарных исходов.

Ответ: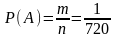

5. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго — 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

Решение:

Обозначим попадание в цель первым стрелком – событие А, вторым – событие В, промах первого стрелка – событие 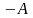, промах второго – событие 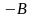. Тогда

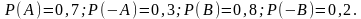
Вероятность того, что первый стрелок попадет в мишень, а второй – нет, равна:

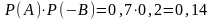
Вероятность того, что второй стрелок попадет в цель, а первый – нет, равна:

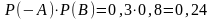
Тогда вероятность попадания в цель только одним стрелком равна:

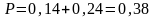
Ответ: 0,38

6. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем пять из них в переплете. Библиотекарь берет наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.

Решение:

Событие А (хотя бы один из взятых трех учебников имеет переплет) и Ā (ни один из взятых учебников не имеет переплета) – противоположные.

Найдем общее число возможных элементарных исходов испытания:

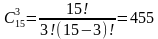
Определим число исходов, благоприятствующих событию Ā:

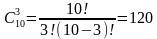
Вероятность события Ā:

Вероятность события А:

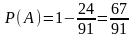
Ответ:

7. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго — 0,9. Найти вероятность того, что взятая наудачу деталь окажется стандартной.

Решение:

Рассмотрим следующие гипотезы: H₁ – деталь взята из первого ящика, H₂ – деталь взята из второго ящика. Из условия задачи следует, что все гипотезы равновозможные, то есть:

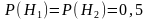
Подставляя значения и в формулу полной вероятности, находим:

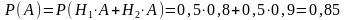
Ответ:

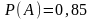
8. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму — 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым — 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.

Решение:

Рассмотрим следующие гипотезы: H₁ – деталь проверена первым контролером, H₂ – деталь проверена вторым контролером. Из условия задачи следует:

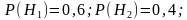
Найдем 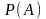по формуле полной вероятности и 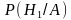по формуле Байеса:

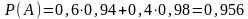
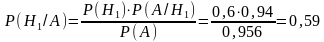
Ответ:

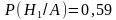
9. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются)?

Решение:

Так как шахматисты по условию равносильные, а ничьи не учитываются, считаем, что выигрыш и проигрыш может наступить с равной вероятностью. Поэтому

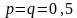
Воспользуемся формулой Бернулли:

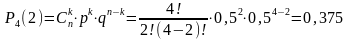
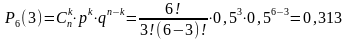
Так как P₄(2) > P₆(3) вероятнее выиграть 2 партии из 4.

Ответ: 2 партии из 4.

10. Найти вероятность того, что событие А наступит 1400 раз в 2400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,6.

Решение:

Так как n = 2400 велико, p = 0,6, q = 0,4 не малы, k = 1400, применяем интегральную формулу Муавра-Лапласа. Определяем x:

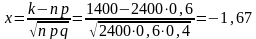
Так как функция 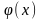является четной, следовательно, В таблице значений функции найдем значение:

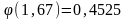
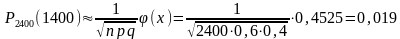
Ответ: 0,019