7Корреляция

ЛЕКЦИЯ 14. ЛИНЕЙНАЯ КОРРЕЛЯЦИЯ

Функциональная и статистическая зависимости. Две случайные величины могут быть связаны

1. функционально (изменение одной из них влечёт соответствующее изменение другой),

2. статистически (изменение одной из них влечёт изменение закона распределения другой).

3. Две случайные величины могут быть независимыми.

Статистическую зависимость, при которой изменение одной случайной величины вызывает изменение среднего значения другой, называют корреляционной или регрессионной.

Например, пусть СВ – посещаемость студентами учебных занятий, – успеваемость. Понятно, что не является функцией от . Но, как показывает опыт, результаты экзаменационной сессии лучше у тех студентов, которые систематически посещали учебные занятия. Это значит, что связана с корреляционно.

Чтобы уточнить определение корреляционной зависимости, рассмотрим условные моменты.

Определение 16.1. Условным математическим ожиданием при называется выражение вида:

– для ДСВ ,

– для НСВ .

Аналогично определяется условное математическое ожидание при :

– для ДСВ ,

– для НСВ .

Определение 16.2. Корреляционной зависимостью СВ от СВ называется функциональная зависимость условного матожидания от :

– функция регрессии на ,

– уравнение регрессии на ,

график функции – линия регрессии на .

Аналогично определяется корреляционная зависимость от , функция регрессии СВ на СВ и уравнение регрессии СВ на СВ .

Примеры корреляционной зависимости:

1. вес и рост человека – с увеличением роста вес в среднем также увеличивается (рост является фактором веса);

2. надёжность автомобиля и срок его эксплуатации – чем больше срок эксплуатации, тем меньше надёжность (срок эксплуатации автомобиля – фактор его надёжности).

Для полного анализа корреляционной зависимости между двумя случайными величинами и нужно выяснить

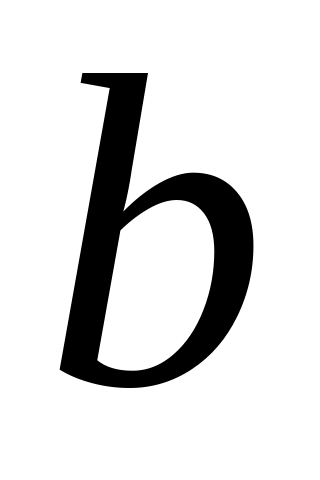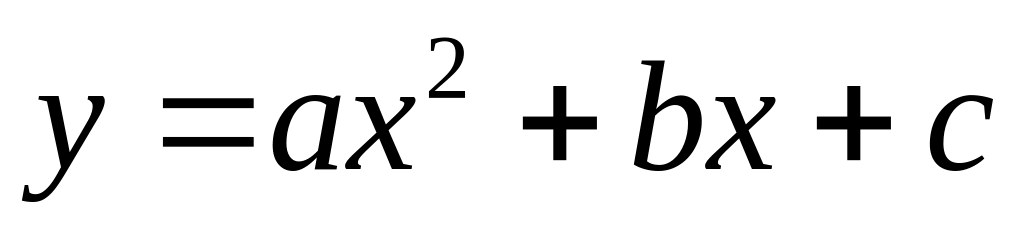1. её вид и параметры (например, линейная регрессия с параметрами и , квадратичная регрессия с параметрами , и и т.п.);

2. тесноту (силу).

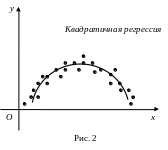
Вид корреляционной зависимости определяют исходя из анализа расположения точек , , на корреляционном поле (рис. 1, 2).

Определение 16.3. Корреляционное поле – это изображение полученных в результате опыта данных , , в виде точек в декартовой системе координат, где на оси абсцисс откладывают значения независимой переменной, а на оси ординат – значения зависимой переменной.

П араметры корреляционной зависимости можно находить, например, методом наименьших квадратов, который усредняет, сглаживает опытные данные.

Теснота корреляционной зависимости от оценивается рассеиванием значений около . Большое рассеивание означает слабую зависимость от , либо отсутствие зависимости. Малое рассеивание указывает на существование достаточно сильной зависимости.

Важной в приложениях является ситуация, когда обе функции регрессии и являются линейными. Тогда случайные величины и связаны линейной корреляционной зависимостью (линейной корреляцией). Так будет, если двумерная СВ имеет совместное нормальное распределение.

Корреляционное отношение. Пусть СВ зависит в основном от фактора и некоторого остаточного (небольшого по величине) фактора в виде СВ , которая влияет на , но не на .

Характеристикой общей изменчивости СВ является её дисперсия . В эту величину вносят вклад фактор и СВ . При фиксированном дисперсия

характеризует влияние на остатка , а её среднее значение

характеризует влияние в целом остатка на . Обозначим

.

Математическое ожидание – это центр группирования значений СВ при , – общий центр группирования . Поэтому разброс групповых центров относительно общего центра определяется дисперсией

,

которая характеризует изменчивость значений под влиянием фактора . Обозначим

.

Можно показать, что

.

Обозначим

.

Величина показывает, какая доля вариации значений СВ обусловлена вариацией значений фактора , и называется коэффициентом детерминации, а называется корреляционным отношением.

Свойства корреляционного отношения

1. .

2. Условие необходимо и достаточно для функциональной зависимости от .

Действительно, при имеем . Так как , то при любом . Это значит, что есть константа при любом значении фактора , то есть есть функция от .

Наоборот, если есть функция от , то для любого , поэтому .

3. Условие необходимо и достаточно для отсутствия регрессионной зависимости от .

Действительно, при имеем

.

Поэтому есть константа при любом и, значит, нет регрессионной зависимости от . Обратное очевидно.

4. Чем ближе к единице, тем ближе статистическая зависимость от к функциональной, и наоборот – чем ближе зависимость от к функциональной, тем ближе к единице.

►Пример. Двумерная СВ имеет следующий закон распределения

	-3	0	3
-2	0,4	0,1	0
2	0	0,1	0,4

Найти коэффициент детерминации и корреляционное отношение между и .

Решение. Найдём ряд распределения СВ и , :

	-3	0	3
	0,4	0,2	0,4

.

.

Найдём условные законы распределения и .

Вычислим вероятности значений СВ при :

,

,

.

Условие нормировки: .

	-3	0	3
	0,8	0,2	0

Вычислим вероятности значений СВ при :

,

,

.

Условие нормировки: .

	-3	0	3
	0	0,2	0,8

Найдём условные математические ожидания:

;

.

Вычислим условные дисперсии:

,

.

Получаем

.

Значит, коэффициент детерминации равен

,

корреляционное отношение

.

Поскольку близко к единице, то зависимость от близка к функциональной. Действительно, из таблицы, в которой дан закон распределения СВ , видно, что при данном значении с большой вероятностью соблюдается равенство . ◄

ЛЕКЦИЯ 15. ЛИНЕЙНАЯ СРЕДНЕКВАДРАТИЧНАЯ РЕГРЕССИЯ. ЛИНЕЙНАЯ РЕГРЕССИЯ

Линейная среднеквадратичная регрессия. Рассмотрим двумерную СВ , в которой составляющие и зависимые. Предположим, что вид зависимости от неизвестен.

Построим линейную аппроксимацию зависимости СВ от СВ . Подберём параметры и линейной функции

так, чтобы

.

Функция называется линейной среднеквадратичной регрессией на .

Исследуем функцию на минимум. Сначала преобразуем её:

.

Затем найдём частные производные по и :

,

.

Приравнивая их нулю, получаем следующую систему уравнений

Решив её, получаем

, .

С учётом того, что ковариация

,

где – коэффициент корреляции, , , получаем искомую линейную зависимость

.

Полученное уравнение задаёт среднеквадратичную регрессию на .

Можно показать, что при полученных значениях и величина (ошибка приближения линейной среднеквадратичной регрессии) равна

,

а ошибка регрессии

.

Отсюда следует, что

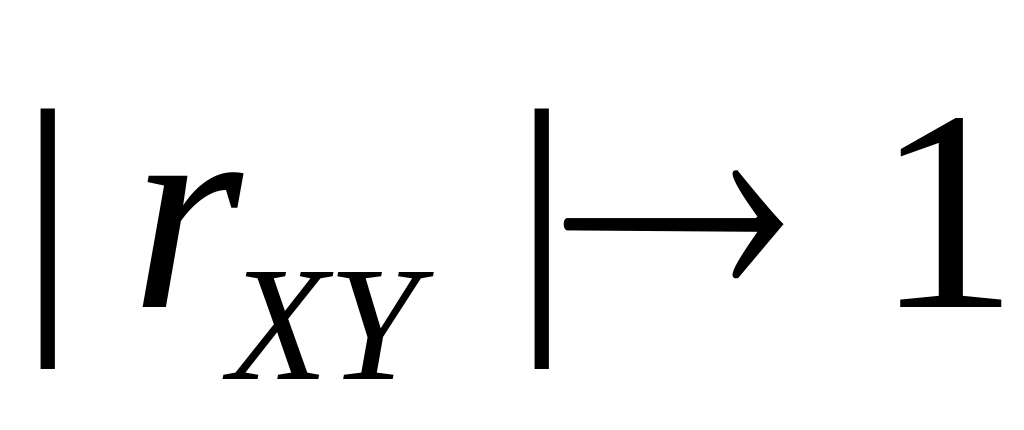1. если , то уменьшается ошибка приближения, то есть возрастает концентрация значений СВ около среднеквадратичной зависимости на . Обратное также верно. Поэтому показывает степень линейной функциональной зависимости между случайными величинами и .

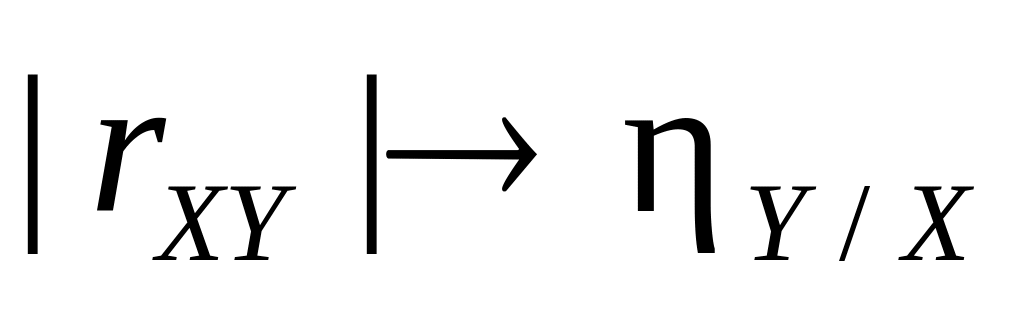2. если , то уменьшается ошибка регрессии, то есть неизвестная функция регрессии приближается к среднеквадратичной зависимости на . Верно и обратное. В частности, в случае линейной корреляции , то есть ошибка регрессии равна 0. Поэтому разность можно использовать в качестве меры отклонения функции регрессии от линейной.

Допустим, распределение СВ неизвестно, но имеются результаты наблюдений, то есть выборка значений СВ . Тогда все рассмотренные величины заменим их выборочными аналогами и найдём и из следующей системы уравнений

где 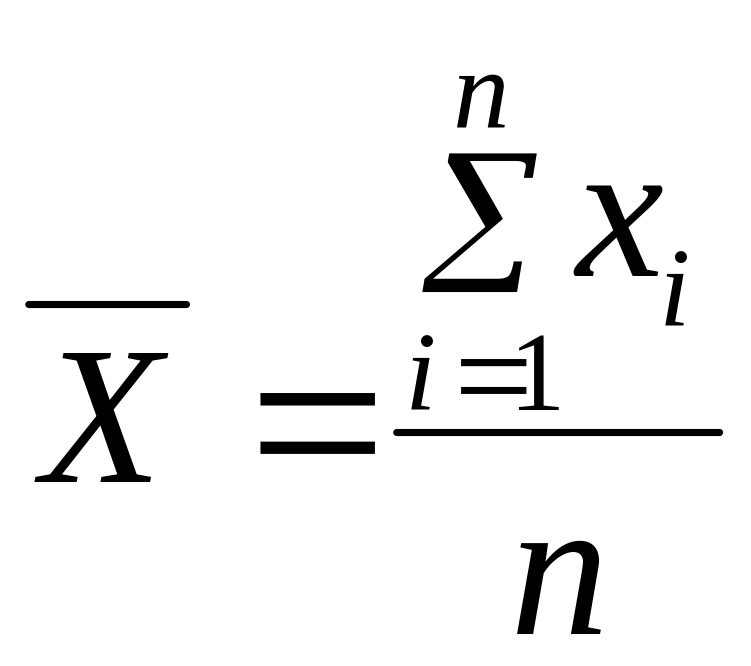, – выборочные средние; , .

Решив систему, получим

,

.

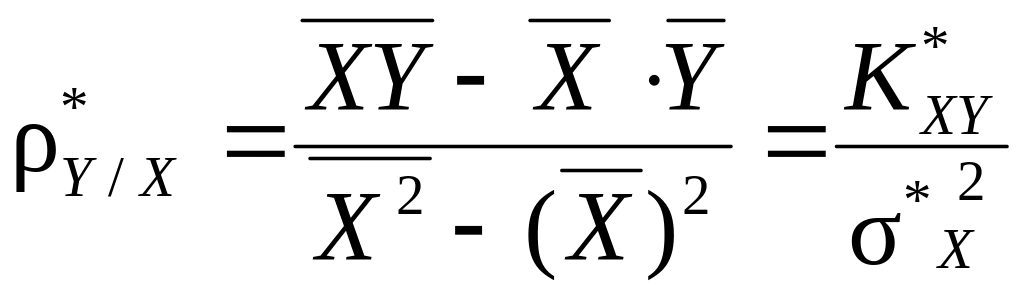где , – выборочные аналоги корреляционного момента и дисперсии соответственно.

Следовательно, выборочное уравнение прямой среднеквадратичной регрессии на имеет вид

.

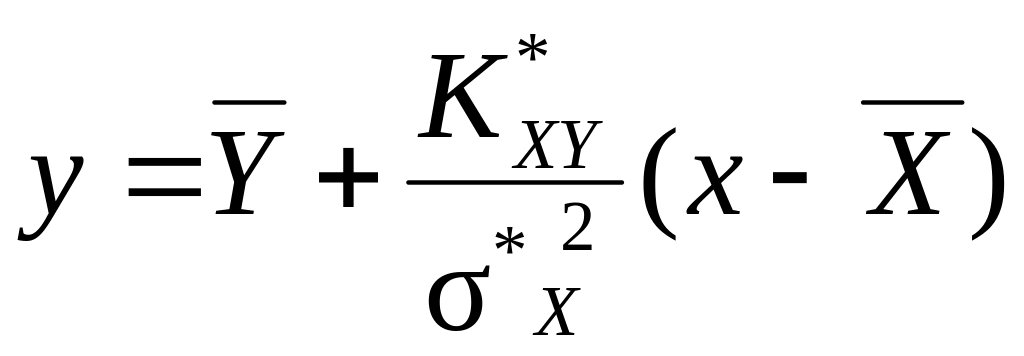Это уравнение наилучшим образом в классе линейных моделей описывает опытную зависимость от . Его можно использовать для прогнозирования значений как функции .

Коэффициент в выборочном уравнении среднеквадратичной регрессии на называется статистическим коэффициентом регрессии на . Он является мерой, которая на основании выборочных данных в среднем указывает влияние изменения независимой переменной (или ) на зависимую переменную (или ).

Аналогично получается уравнение прямой среднеквадратичной регрессии на :

,

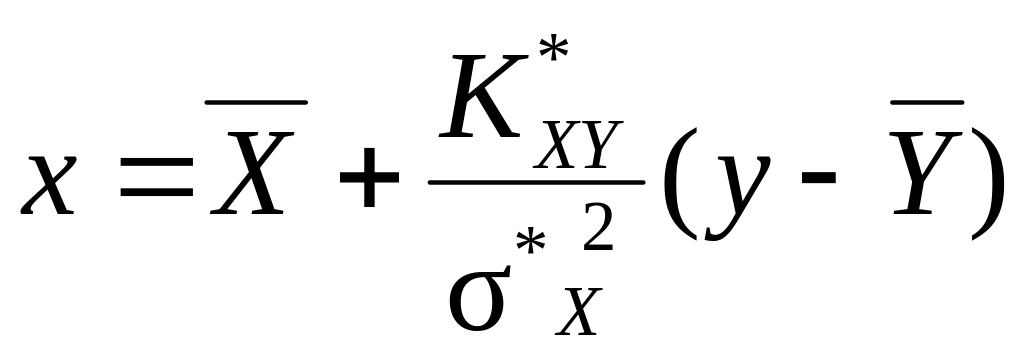где статистический коэффициент регрессии на определяется формулой

.

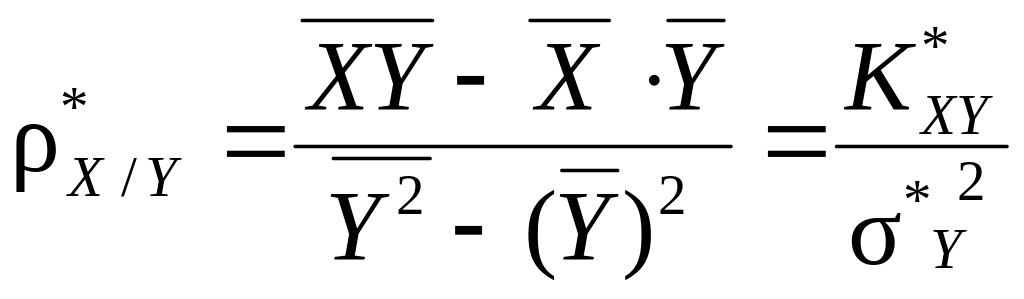►Пример. Определить выборочное уравнение прямой среднеквадратичной регрессии на , если СВ – обеспеченность рабочей силой, СВ – производство продукции на 100 га сельскохозяйственных угодий в 15 сельскохозяйственных предприятиях Витебской области на основании данных, приведенных в таблице 1.

Таблица 1

№ п/п	Средняя численность работников на 100 га сельхозугодий, чел. ( )	Валовая продукция на 100 га сельхозугодий, млн руб. ( )
1	7,2	199
2	16,9	513
3	10,7	178
4	6,9	212
5	9,5	271
6	11,6	215
7	8,9	145
8	10,2	336
9	7,8	251
10	4,8	195
11	7,4	275
12	10,0	319
13	9,6	375
14	6,6	232
15	5,8	242
Сумма	133,9	3958

Решение. Составляем расчётную таблицу 2.

Таблица 2

	Средняя численность работников на 100 га сельхозугодий, чел. ( )	Валовая продукция на 100 га сельхозугодий, млн руб. ( )
1	7,2	199	1432,8	51,84	39601
2	16,9	513	8669,7	285,61	263169
3	10,7	178	1904,6	114,49	31684
4	6,9	212	1462,8	47,61	44944
5	9,5	271	2574,5	90,25	73441
6	11,6	215	2494,0	134,56	46225
7	8,9	145	1290,5	79,21	21025
8	10,2	336	3427,2	104,04	112896
9	7,8	251	1957,8	60,84	63001
10	4,8	195	936,0	23,04	38025
11	7,4	275	2035,0	54,76	75625
12	10,0	319	3190,0	100,0	101761
13	9,6	375	3600,0	92,16	140625
14	6,6	232	1531,2	43,56	53824
15	5,8	242	1403,6	33,64	58564
Сумма	133,9	3958	37909,7	1315,61	1164410