6Системы Случайных Величин

РАЗДЕЛ V. ДВУМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

ЛЕКЦИЯ 11. ЗАКОН РАСПРЕДЕЛЕНИЯ ДВУМЕРНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

Понятие о системе случайных величин. Иногда в практических задачах результат опыта описывается не одной случайной величиной (её возможные значения определялись одним числом), а двумя или более случайными величинами, образующими систему (их возможные значения определяются несколькими числами).

Например,

– точка попадания снаряда описывается абсциссой и ординатой. Получаем систему двух случайных величин.

– Осколок, образовавшийся при разрыве снаряда, характеризуется весом, размерами, начальной скоростью, направлением полета. Получаем систему четырех случайных величин.

С истема двух случайных величин и обозначается – двумерная случайная величина.

Геометрически её можно изобразить случайной точкой на плоскости координатами или случайным радиус-вектором с координатами конца (рис. 1).

Свойства системы случайных величин включают в себя свойства отдельных составляющих, а также взаимные связи между ними.

Системы случайных величин могут быть дискретными, непрерывными или смешанными в зависимости от типа их одномерных составляющих.

Закон распределения двумерной дискретной случайной величины

Как и в случае одномерной случайной величины, полной вероятностной характеристикой двумерной случайной величины является закон распределения – соотношение, устанавливающее связь между областями её возможных значений и вероятностями её появления в этих областях.

Определение 12.1. Законом распределения двумерной ДСВ называется множество всех её возможных значений с их вероятностями.

Этот закон записывается в виде таблицы с двойным входом:

			…		…
			…		…
			…		…
…	…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…	…
			…		…
			…		…		1

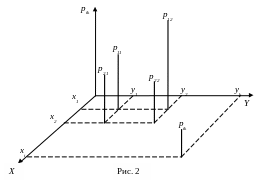
Графическая форма задания закона распределения двумерной ДСВ приведена на рис. 2.

►Пример. Двумерная ДСВ задана законом распределения

Х Y	2	3	4
2	0,3	0,15	0,05
3	0,15	0,10	0,05
4	0,05	0,05	0,05
5	0,05	0	0

Найти законы распределения составляющих и .

Решение. Сложив вероятности по столбцам, получим вероятности возможных значений ДСВ :

,

,

,

.

Закон распределения составляющей :

	2	3	4	5
	0,50	0,30	0,15	0,05

– условие нормировки выполнено.

Сложив вероятности по строкам, аналогично найдём распределение составляющей :

	2	3	4
	0,55	0,30	0,15

– условие нормировки выполнено. ◄

Функция распределения двумерной случайной величины. Универсальной характеристикой многомерных случайных величин дискретных и непрерывных является функция распределения.

О пределение 12.2. Функцией распределения двумерной случайной величины называется вероятность совместного выполнения двух неравенств и :

.

Геометрически функция распределения есть вероятность попадания точки в бесконечный квадрат с вершиной в точке , лежащий левее и ниже ее (рис.3).

Из определения следует, что для двумерной ДСВ :

,

где суммирование выполняется по всем точкам , для которых одновременно и .

►Пример. Передаются два сообщения, каждое из которых может быть независимо от другого принято с искажением или без искажения. Вероятность того, что первое (второе) сообщение принято с искажением, равна 0,1 (0,15). Рассмотрим двумерную случайную величину , составляющие которой имеют следующие множества значений:

Найти распределение двумерной случайной величины и её функцию распределения .

Решение. Составляющие двумерной случайной величины дискретны, поэтому вероятности возможных пар значений равны:

,

,

,

.

Соответствующая таблица имеет вид:

X Y	0	1
0	0,765	0,085	0,85
1	0,135	0,015	0,15
	0,9	0,1	1

Тогда

◄

Свойства функции распределения двумерной случайной величины

1. Функция распределения – неубывающая:

если , то , если , то .

Докажем, что – неубывающая функция по , то есть, что

при или .

Событие при состоит из суммы двух событий: « принимает значение, меньшее при » с вероятностью и « принимает значение, удовлетворяющее неравенству при » с вероятностью . Эти события несовместны, поэтому

.

Так как вероятность – число положительное, то

.

2. Повсюду на .

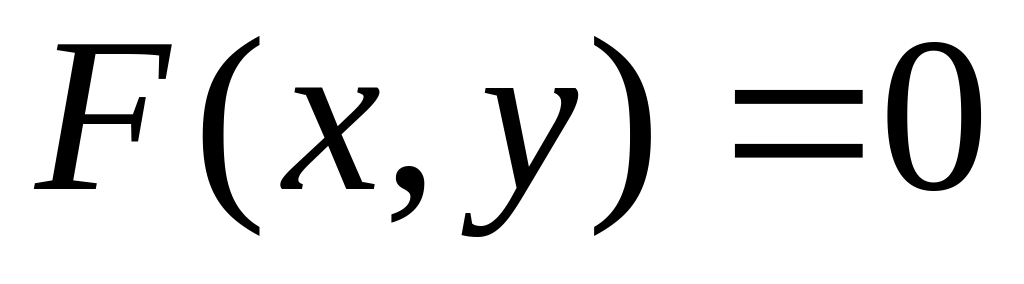При – вероятность события . Это событие невозможное, поэтому и т.д.

3. Если оба аргумента равны , то .

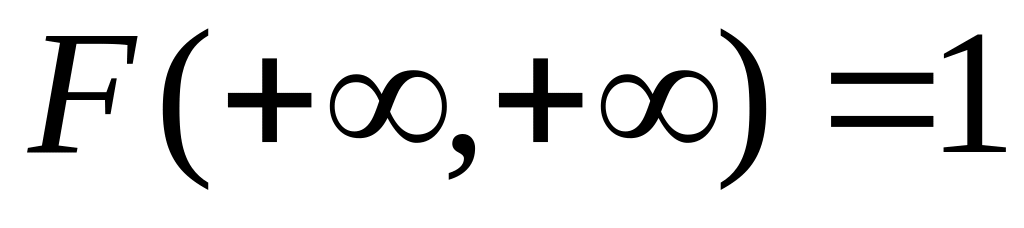Действительно, событие – достоверное, поэтому .

4. При одном из аргументов, равном , функция распределения равна функции распределения другого аргумента:

, .

Действительно, событие достоверное, поэтому

.

Аналогично, событие достоверное, поэтому

.

Геометрически функция есть вероятность попадания случайной точки в полуплоскость, ограниченную справа абсциссой (рис. 4), а – вероятность попадания случайной точки в полуплоскость, ограниченную сверху ординатой (рис. 5).

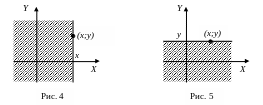
5. Функция распределения двумерной случайной величины непрерывна слева по каждому аргументу.

С помощью свойств двумерной функции распределения можно вычислить вероятность попадания двумерной случайной величины в любую прямоугольную область, поэтому справедливы следующие теоремы.

Теорема 12.1. Вероятность попадания случайной точки в бесконечную полуполосу равна приращению функции распределения по одному из аргументов (рис. 6, 7):

,

.

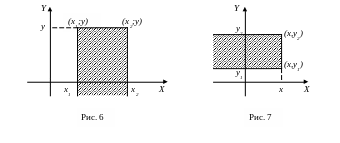Доказательство. Из геометрической интерпретации двумерной функции распределения видно, что

или по определению 12.2

,

откуда следует, что

.

Аналогично доказывается равенство

.

Теорема 12.2. Вероятность попадания случайной точки в прямоугольник (рис. 8) равна:

.

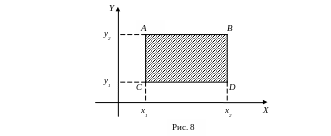
Эта вероятность находится вычитанием из вероятности попадания случайной точки в полуполосу вероятности попадания случайной точки в полуполосу (рис. 8).

►Пример. Задана функция распределения двумерной случайной величины

Найти вероятность попадания случайной точки в прямоугольник, ограниченный прямыми , , , .

Решение. Положив , , , , получим

. ◄

Двумерная непрерывная случайная величина. Плотность вероятности двумерной случайной величины. Функция распределения характеризует как дискретные так и непрерывные двумерные случайные величины. Но последние ещё удобно задавать плотностью вероятности.

П лотность вероятности одномерной случайной величины есть предел отношения вероятности попадания её значений на малый участок к длине этого участка при неограниченном уменьшении этой длины. Для системы двух случайных величин определение плотности вероятности аналогичное: вероятность попадания случайной точки в прямоугольник со сторонами и , примыкающий к точке (рис. 9).

Найдём вероятность попадания случайной точки в :

.

Разделим вероятность попадания случайной точки в прямоугольник на его площадь и найдём предел этого выражения при и :

.

Предполагая, что непрерывна и дифференцируема, и применив теорему Лагранжа, получим

,

где точка расположена между и , точка – между и .

Тогда

,

так как при и , .

Определение 12.3. Функция , равная пределу отношения вероятности попадания двумерной случайной величины в прямоугольник со сторонами и к площади этого прямоугольника, когда и , называется плотностью вероятности.

Таким образом,

во всех точках, где существует смешанная производная.

Геометрически функция изображается некоторой поверхностью, которая аналогична по смыслу кривой распределения и называется поверхностью распределения.

Если её пересечь плоскостью, параллельной плоскости и спроецировать полученное сечение на , то получится кривая, в каждой точке которой плотность вероятности постоянна (кривая равной плотности).

По аналогии с одномерным случаем рассмотрим понятие элемента вероятности. Из определения предела следует, что

,

где при , .

Определение 12.4. Элементом вероятности двумерной случайной величины называется выражение , которое даёт вероятность попадания случайной точки в элементарный прямоугольник со сторонами и , примыкающий к точке .

Эта вероятность равна объёму элементарного параллелепипеда, ограниченного сверху поверхностью и опирающегося на элементарный прямоугольник .

Найдём теперь вероятность попадания двумерной НСВ в произвольную область . Для этого разобьем на элементарных прямоугольников и выберем в каждом из них точку .