5Закон больших чисел

РАЗДЕЛ IV. ЗАКОН БОЛЬШИХ ЧИСЕЛ

ЛЕКЦИЯ 10. НЕРАВЕНСТВА ЧЕБЫШЕВА. ПОНЯТИЕ О ЦЕНТРАЛЬНОЙ ПРЕДЕЛЬНОЙ ТЕОРЕМЕ

Под законом больших чисел понимают общий принцип, в силу которого совместное действие случайных факторов приводит при определённых весьма общих условиях к результату, почти не зависящему от случая. Этот принцип выражается рядом теорем. В их числе – теорема Бернулли, теорема Чебышева. Для доказательства этих теорем используется

Неравенства Чебышева.

Вероятность того, что абсолютная величина отклонения СВ от своего математического ожидания меньше положительного числа, не меньше разности :

или .

Докажем теорему для ДСВ , имеющей закон распределения , .

События и являются противоположными, поэтому сумма их вероятностей равна единице, то есть

,

откуда

.

Дисперсия ДСВ равна:

.

Предположим, что значения случайной величины занумерованы так, что

, , …, ,

, , …, .

Поскольку обе части каждого из последних неравенств положительны, то

, , …, .

Понятно тогда, что

.

В соответствии с теоремой сложения вероятностей независимых событий сумма выражает вероятность того, что ДСВ примет одно из значений , , для которого , то есть

.

Поэтому

,

откуда

– первое неравенство Чебышева.

Найдем :

–

второе неравенство Чебышева.

Доказательство для непрерывных случайных величин аналогичное. Дисперсия НСВ :

.

Разобьем область интегрирования на три части:

, , .

Тогда

.

Опустив средний интеграл, получаем неравенство:

.

В пределах каждой из областей интегрирования

.

Значит,

.

Отсюда следует

.

Неравенство Чебышева имеет прежде всего теоретическое значение. Но когда о законе распределения случайной величины мало информации, оно находит практическое применение.

►Пример. Оценить вероятность того, что отклонение какой-либо случайной величины от её математического ожидания по модулю будет меньше трёх среднеквадратических отклонений этой величины.

Решение. Пусть – случайная величина и . Тогда

.

В случае нормально распределённой случайной величины эта вероятность равна 0,9973, что не противоречит полученному результату. ◄

Второе неравенство Чебышева даёт верхнюю границу для вероятности того, что будет превышение некоторого заданного числа среднеквадратических отклонений независимо от вида закона распределения.

Теорема Чебышева. Случайная величина принимает значения, зависящие от многих причин. Учесть эти причины полностью невозможно. Поэтому и невозможно заранее указать значение, которое случайная величина примет в результате данного опыта. На первый взгляд кажется, что поведение суммы достаточно большого числа случайных величин не обладает закономерностью, как и каждая случайная величина в отдельности. Но это не так. Поведение суммы достаточно большого числа случайных величин при некоторых условиях перестает быть случайным и становится закономерным. Эти условия указаны в теореме Чебышева.

Рассмотрим случайную величину , закон распределения которой меняется от опыта к опыту. Тогда появляются несколько ( ) случайных величин.

Если случайные величины , , …, независимы, имеют математические ожидания и дисперсии, каждая из которых ограничена одним и тем же числом , то для любого положительного числа выполняется неравенство:

.

Cреднее арифметическое данных случайных величин имеет вид:

.

Тогда

.

Применяя второе неравенство Чебышева к СВ , получаем:

.

Учитывая условие ( ) и свойства дисперсии, находим

,

.

Из последнего неравенства и второго неравенства Чебышева следует неравенство:

.

Рассмотрим понятие сходимости по вероятности. Последовательность случайных величин , , …, сходится по вероятности к СВ , если для любого числа :

.

Обозначение сходимости по вероятности:

.

Если случайные величины , , …, удовлетворяют условиям теоремы Чебышева, то

,

,

но так как вероятность не может быть больше единицы, то

.

Теорема Чебышева лежит в основе выборочного метода в статистике. Результат каждого измерения – случайная величина с матожиданием, равным истинному значению измеряемой величины (если нет систематической погрешности). Теорема Чебышева говорит о том, что при большом числе измерений в качестве истинного можно принять среднее арифметическое (вероятность ошибиться при этом тем меньше, чем больше ).

►Пример. Сколько раз нужно измерить величину с истинным значением , чтобы с вероятностью, не меньшей 0,95, можно было утверждать, что среднее арифметическое этих измерений отличается от по модулю меньше, чем на 2, если СКО измерений меньше 10?

Решение. Нужно найти число , удовлетворяющее неравенству

,

где , . Тогда

, , ,

, ,

.

Таким образом, измерять нужно не менее 500 раз. ◄

Если , , то есть – среднее арифметическое случайной величины с равными дисперсиями, то и из неравенства Чебышева следует, что

.

Например, в схеме Бернулли

, где или 1,

, ,

тогда

.

Оценкой можно пользоваться, если под рукой нет таблицы значений функции (интегральная теорема Лапласа).

для .

Пусть, например, , , . Тогда

, ,

, .

►Пример. При штамповке деталей брак в среднем составляет 3%. Оценить вероятность того, что в партии из 1000 деталей число бракованных отклонится от своего среднего значения не более чем на 1%.

Решение. Имеем , , , . Тогда

.◄

Теорема Бернулли. В статистическом определении вероятности наступления события использовалось свойство устойчивости относительной частоты наступления этого события при увеличении числа испытаний. Теоретическим обоснованием этого свойства является теорема Бернулли.

Если – число появлений события в независимых испытаниях и – вероятность появления события в каждом испытании, то вероятность того, что модуль отклонения относительной частоты от вероятности меньше любого числа , больше чем разность , то есть

.

Отсюда следует, что при достаточно больших вероятность как угодно близка к единице, то есть

.

Пусть – число появлений события при -том испытании, . Каждая из случайных величин может принимать лишь два возможных значения: с вероятностью (событие наступило) и с вероятностью (событие не наступило). Поэтому все они имеют одно и то же математическое ожидание

,

одну и ту же дисперсию

.

Поскольку

,

(так как произведение принимает наибольшее значение при ), к случайным величинам применима теорема Чебышева:

.

Так как , имеем:

.

Так как , где – число появлений события при испытаниях, то

.

Заметим, что теорема Бернулли не позволяет утверждать, что неравенство

будет выполнятся для всех достаточно больших . Она лишь утверждает, что выполнение такого неравенства при достаточно больших будет очень вероятно.

►Пример. Начиная с какого числа независимых испытаний выполняется неравенство

,

если в отдельном испытании ?

Решение. Неравенство

в данном случае имеет вид

.

Поэтому

.

Отсюда находим

, , .

Таким образом,

. ◄

Неравенство Маркова

Если СВ принимает только положительные значения и существует её математическое ожидание, то для любого числа справедливо неравенство

.

►Пример. Среднее число молодых специалистов, ежегодно направляемых в аспирантуру, составляет 200 человек. Оценить вероятность того, что в данном году будет направлено в аспирантуру не более 220 молодых специалистов.

Решение. Имеем , . Тогда

,

. ◄

Теорема Пуассона. Пусть производится независимых испытаний, причем вероятности появления события в каждом из них различны и равны , , …, , тогда средняя вероятность имеет вид . Теорема Пуассона утверждает, что

,

где – число испытаний, в которых появилось событие .

Центральная предельная теорема Ляпунова. Многие задачи теории вероятностей связаны с изучением суммы независимых случайных величин. В соответствии с этой теоремой плотность вероятности суммы независимых или слабо зависимых, равномерно малых (играющих одинаковую роль) слагаемых при неограниченном увеличении их числа как угодно близко приближается к нормальному закону распределения независимо от того, какие законы распределения имеют эти слагаемые.

Из теоремы Ляпунова следует локальная теорема Лапласа. Пусть СВ – число появлений события при независимых опытах. Её можно представить так:

,

где – число появлений события при -том испытании, При всех

, (смотри лекцию 7),

то величины ( ) удовлетворяют условиям теоремы Ляпунова. Их сумма имеет распределение, близкое к нормальному. Оно определяется формулой

.

Известно, что

, (смотри лекцию 7).

Тогда при , , получаем

.

Поэтому верна локальная теорема Лапласа: если вероятность появления события в каждом из независимых испытаний равна одной и той же постоянной ( ), то вероятность того, что во всех этих испытаниях событие появится ровно раз, приближённо выражается формулой

или

при , где .

Приведём без доказательства интегральную теорему Лапласа: если вероятность появления события в каждом из независимых испытаний равна одной и той же постоянной ( ), то вероятность того, что в этих испытаниях событие появится не менее раз и не более , приближённо выражается формулой

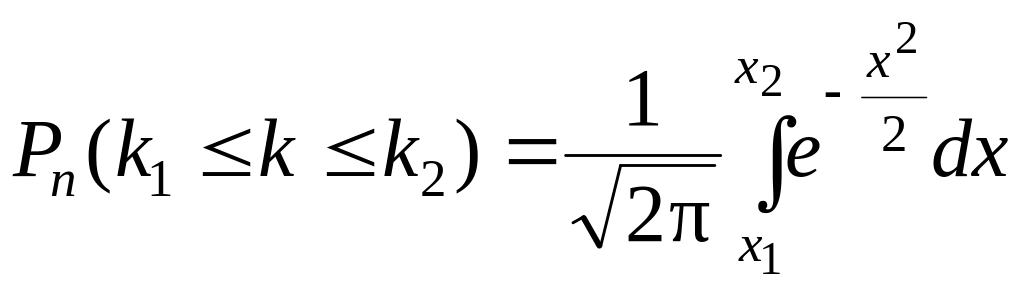, где , .

Эта формула имеет другой вид:

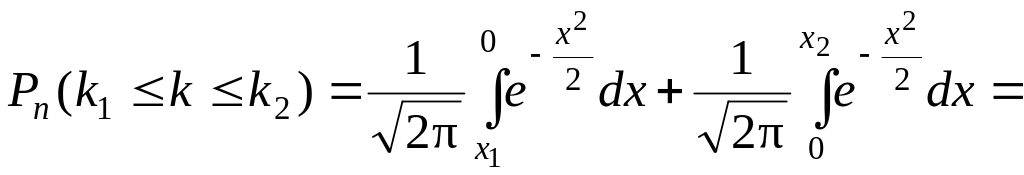
или

, где – функция Лапласа.

98