2Случ События

.

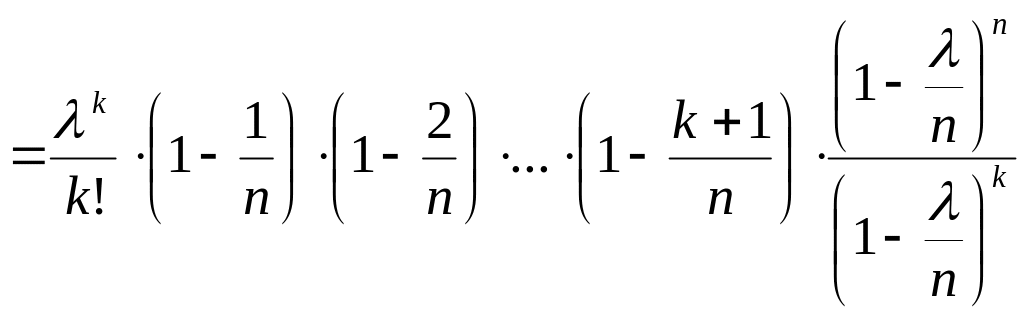Заметим, что – второй замечательный предел. Поэтому

при ,

то есть

.

Полученное приближённое равенство называется формулой Пуассона.

Вероятность события, заключающегося в том, что событие появится не более раз, очевидно, вычисляется по формуле

.

►Пример. При транспортировке и разгрузке керамической отделочной плитки повреждается 2,5%. Найти вероятность того, что в партии из 200 плиток поврежденными окажутся: а) ровно 4; б) не более 6.

Решение. Поскольку вероятность повреждения плитки мала, число плиток – достаточно большое и , можно воспользоваться формулой Пуассона:

;

.◄

Локальная и интегральная формулы Муавра-Лапласа

При достаточно большом и не слишком малых и ( ) формула Пуассона дает значительную погрешность и применяется другое приближение формулы Бернулли – локальная формула Муавра-Лапласа, которую можно получить из формулы Бернулли, совершая предельный переход и применяя формулу Стирлинга для вычисления :

, где .

, где , .

Эта формула табулирована (приложение 1), причем в силу четности функции , таблица ее значений составлена для .

Если при сохранении условий предыдущего пункта нас интересует вероятность того, что при испытаниях событие появится не менее и не более раз, то формула Бернулли с учетом предельного перехода превращается в интегральную формулу Муавра-Лапласа.

,

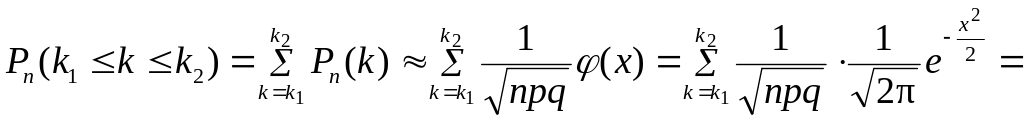
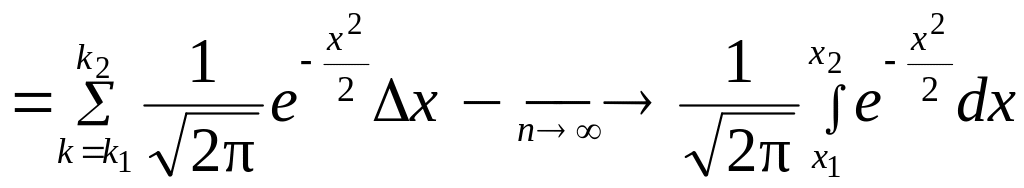где

, .

Обозначим 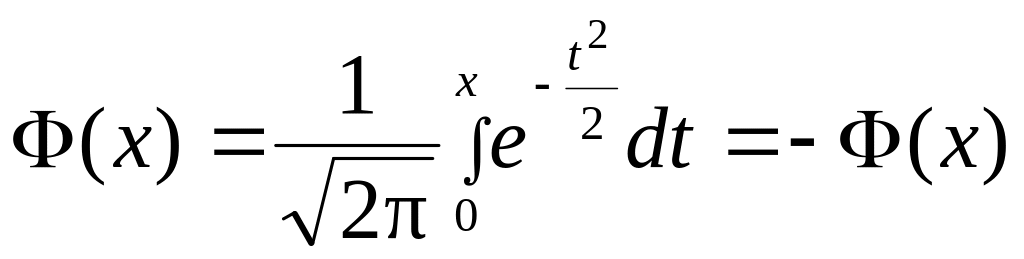(интеграл от чётной функции – функция нечётная). Тогда

,

где

, , .

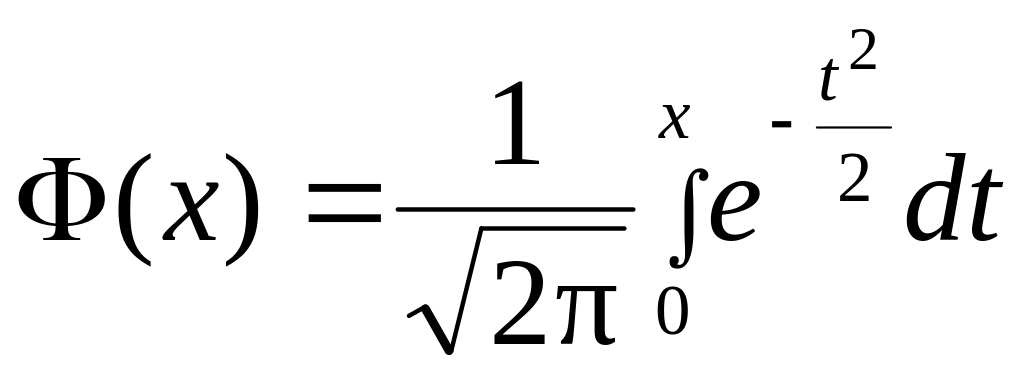Функция (интеграл от ) называется функцией Лапласа и представляет собой не выражающийся через элементарные функции интеграл. Поскольку функция Лапласа нечетная ( ) и быстро приближается к своему асимптотическому значению 0,5, то таблица ее значений (приложение 2) составлена для . Для больших значений аргумента ( ) с большой точностью можно брать .

►Пример. Вероятность того, что зашедший в ресторан посетитель сделает заказ, равна 0,8. Найти вероятность того, что из 100 зашедших не менее 75 сделают заказ.

Решение. Так как велико, , не малы, , , применяем интегральную формулу Муавра-Лапласа. Определяем и :

, .

С помощью таблицы значений функции Лапласа находим:

, .

Наконец, получаем искомую вероятность:

.◄

Оценим вероятность того, что относительная частота события отклоняется от его статистической вероятности не более чем на , то есть найдём .

Рассмотрим неравенство :

,

,

,

.

Отсюда

для .

►Пример. В среднем число солнечных дней в году для данной местности равно 100. Найти вероятность того, что в данном году их число отклонится от среднего не более чем на 10.

Решение. По условию , , , , . Тогда

,

.◄

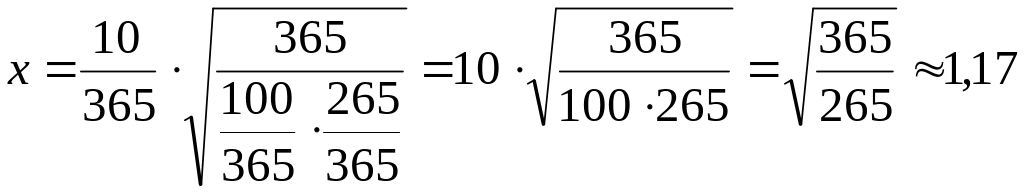1 Г.В. Горелова, И.А. Кацко. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel. Учебное пособие для вузов. Издание 2-е исправленное и дополненное. – Ростов н/Д: Феникс, 2002. – 400 с., ил.

36