1Определение ФДП, предел, непрерывность ФДП

РАЗДЕЛ VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

ЛЕКЦИЯ 1. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ. ЕЁ ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ

Понятие функции двух переменных. В природе часто встречаются зависимости функции от двух переменных и более. Например, функция , выражающая площадь прямоугольника, зависит от двух переменных – длины и ширины : . Функция , выражающая объём параллелепипеда, зависит от трёх переменных – длины , ширины , высоты : . Поэтому расширим понятие функции¹ одной переменной и введём понятие функции нескольких переменных. Все важнейшие факты теории функции нескольких переменных рассмотрим на примере функции двух переменных, так как в этом случае можно привести наглядную интерпретацию.

Пусть задано множество упорядоченных пар чисел .

Определение 1.1. Соответствие (закон) , сопоставляющее каждой паре чисел единственное число , называется функцией двух переменных и .

Обозначение: , , , , .

Переменные и называются независимыми переменными или аргументами, – зависимой переменной или функцией.

Пару значений аргументов удобно изображать точкой на числовой плоскости . Те пары чисел, которые (по условию вопроса) могут быть значениями переменных и функции , составляют область определения этой функции. Геометрически область определения функции представляет собой конечную или б есконечную область плоскости , ограниченную линиями, которые принадлежат (замкнутая область определения) или не принадлежат этой области (открытая область определения).

Например, область определения функции площади прямоугольника есть открытое бесконечное множество точек плоскости (рис. 1), лежащих внутри первой координатной четверти:

(рис. 1).

► Пример. Найти область определения функции

а) ;

б) .

Р ешение. а) Область определения этой функции состоит из всех точек плоскости , для которых , то есть . Искомая область есть круг с центром в начале координат и радиусом 1, включая свою границу – окружность (рис. 2).

б) Область определения этой функции состоит из всех точек плоскости , для которых

или .

Получаем совокупность двух систем неравенств

Выделив полные квадраты в левой части каждого неравенства, получаем

Изобразим графические решения первой (рис. 3) и второй (рис. 4) систем.

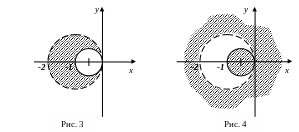
Таким образом, областью определения функции является множество внутренних точек круга радиуса 1 с центром в точке без внутренних точек круга радиуса с центром в точке .◄

Способы задания функции двух переменных. Аналитический. Функцию двух или большего числа переменных можно задать формулой, явно или неявно.

► Пример. 1. Формула , где , выражает зависимость между объёмом одного килограмма воздуха (в м³), его давлением (в ) и температурой (по Цельсию). Каждая из переменных , , есть неявная функция от двух других.

2. Формула задаёт как явную функцию двух аргументов и . Её область определения есть совокупность физически возможных значений давления и температуры: , .

Если физический смысл аргументов не указан, то подразумевается, что область определения охватывает все точки, для которых формула имеет смысл. ◄

Табличный. Функцию двух переменных можно задать таблицей с двойным входом (например, таблица умножения).

Графический. Функцию двух переменных можно представить пространственным графиком, то есть некоторой поверхностью в прямоугольной системе координат . Каждой точке области определения функции соответствует точка , где – аппликата точки . Совокупность всех таких точек и есть поверхность, изображающая данную функцию . Проекция точки поверхности на плоскость изображает пару значений аргументов , аппликата точки изображает соответствующее значение функции .

Т очки, для которых функция имеет одно и то же значение, можно соединить линией. Проекция этой линии на плоскость называется линией уровня.

Например, функция представляется полусферой (рис. 5). В точках выделенной окружности функция имеет постоянное значение. Проекция этой окружности на плоскость является линией уровня данной функции. Множество всех линий уровня данной функции называется картой линий уровня данной функции. По такой карте можно получить довольно точное представление о характере графика исследуемой функции.

Предел функции двух переменных. Множество всех точек плоскости, координаты которых удовлетворяют неравенству

,

называется δ-окрестностью точки (внутренние точки круга с центром и радиусом на рис. 6)².

Пусть функция определена в некоторой окрестности точки . В самой точке функция может быть либо определена, либо нет. Число является пределом функции в точке , если неограниченно приближается к при неограниченном приближении точки к .

Приведем точное определение предела функции .

Определение 1.2. Число называется пределом функции в точке , если абсолютная величина разности остается меньше любого заранее данного положительного числа ε (то есть ) всякий раз, как расстояние меньше некоторого положительного числа , зависящего от (то есть ).

Обозначения:

, .

С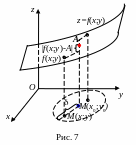 геометрической точки зрения является пределом , если аппликата поверхности отличается от меньше чем на в том случае, когда проекция точки, лежащей на поверхности, попадает внутрь окружности радиуса с центром в точке (рис. 7).

Отметим, что предел существует, если он не зависит от направления стремления точки к (число таких направлений бесконечно, тогда как для функции одной переменной по двум направлениям: слева и справа).

Свойства предела функции двух переменных аналогичны свойствам предела функции одной переменной.

► Пример. Найти

.

Решение.

. ◄

► Пример. Выяснить, имеет ли функция предел при , .

Решение. Будем приближаться к точке по прямым . Если , то . Получили значение предела, зависящее от . Но, так как предел функции не должен зависеть от способа приближения точки к точке , то функция в точке предела не имеет. ◄

Непрерывность функции двух переменных

Определение 1.3. Функция называется непрерывной в точке , если она имеет предел в этой точке и он равен значению функции в :

.

Если условия определения 1.3. не выполняются, то точка называется точкой разрыва функции . Точки разрыва могут образовывать некоторую линию разрыва.

► Пример. Найти точки разрыва функции .

Решение. Знаменатель дроби равен нулю в точках окружности . Следовательно, точки разрыва образуют линию разрыва с уравнением . ◄

1 Пусть и – два произвольных множества действительных чисел. Соответствие (закон) , сопоставляющее каждому числу единственное число , называется функцией.

2 Отметим, что -окрестностью точки является множество точек, расстояние от которых до точки меньше (внутренние точки отрезка длиной с серединой в точке ).

5