
Методичка по Термодинамике и теплотехнике
.pdfМинистерство образования и науки Российской Федерации
Государственное Образовательное Учреждение Высшего Профессионального Образования
Московская Государственная Академия Тонкой Химической Технологии имени М. В. Ломоносова
Кафедра «Процессы и аппараты химической технологии»
Алексеев П. Г., Гаврилова Е. В., Гольцова И. Г.
Техническая термодинамика и теплотехника
(3е издание, дополненное, переработанное)
Методические указания для самостоятельной работы студентов
Москва
2010 год
www.mitht.ru/e-library
УДК 621.1 ББК 31.31
Рецензент: профессор Карташов Э. М. (кафедра ВМ).
Техническая термодинамика и теплотехника: методические указания для самостоятельной работы студентов. Авторы:
Алексеев П. Г., Гаврилова Е. В., Гольцова И. Г. Издание 3-е, перераб. и дополн. – М.: ИПЦ МИТХТ им. М.В. Ломоносова, 2010. – 72 с. Компьютерная верстка: Пономарёв К.А.
Данные методические указания по дисциплине «Техническая термодинамика и теплотехника» предназначены для самостоятельной работы студентов III курса дневного отделения и IV курса вечернего отделения всех направлений и всех специальностей по закреплению теоретического материала изучаемой дисциплины, излагаемой на лекциях в МИТХТ.
Данное методическое пособие состоит из 10 глав, в которых кратко рассматривается теоретическая часть данной дисциплины, приводятся решения некоторых задач и задачи для самостоятельной работы. Теоретическая часть каждой из глав включает в себя необходимые для решения задач аналитические выражения. В подавляющем большинстве задач использована система СИ, но также имеется и ряд задач с использованием внесистемных единиц измерения. В приложении приводятся необходимые для решения задач свойства веществ, а также библиографический список.
Настоящие методические указания являются третьим изданием, существенно переработанным и дополненным. Они утверждены библиотечно-издательской комиссией в качестве учебнометодического пособия.
© МИТХТ им. М. В. Ломоносова
- 2 -
www.mitht.ru/e-library
ОГЛАВЛЕНИЕ.
|
|
|
|
|
|
Глава |
Наименование |
Страница |
|
|
|
|
|
|
|
1 |
Основные положения технической термодинамики. |
5 |
|
|
2 |
Первое начало термодинамики. |
8 |
|
|
3 |
Смеси идеальных газов. |
9 |
|
|
4 |
Теплоёмкость. |
11 |
|
|
5 |
Термодинамические процессы с идеальным газом. |
14 |
|
|
6 |
Второе начало термодинамики. |
19 |
|
|
7 |
Исследование процессов получения сжатого газа в |
26 |
|
|
компрессорах. |
|
||
|
|
|
|
|
|
8 |
Реальные вещества: вода и водяной пар. |
30 |
|
|
9 |
Прямые термодинамические циклы – циклы паро- |
40 |
|
|
турбинных установок. |
|
||
|
|
|
|
|
|
10 |
Обратные термодинамические циклы – циклы хо- |
43 |
|
|
лодильных установок. |
|
||
|
|
Приложение. |
48 |
|
|
|
Библиографический список. |
69 |
|
|
|
|
|
|
- 3 -
www.mitht.ru/e-library

Основные условные обозначения.
|
|
|
|
|
|
Параметр |
Символ |
Единица измерения |
|
|
|
|
|
|
|
Внутренняя энергия |
U, u |
Дж, Дж/кг |
|
|
Газовая постоянная |
R |
Дж/(моль×К), Дж/(кг×К) |
|
|
Давление |
P |
Па, бар, атм, ммHg, мH2O |
|
|
Диаметр |
D, d |
м |
|
|
Количество вещества |
|
моль |
|
|
Количество тепла |
Q, q |
Дж, Дж/кг |
|
|
Масса |
M |
кг |
|
|
Массовая доля |
m |
кг/кг смеси, % |
|
|
Массовая теплоёмкость |
C |
Дж/(кг×К) |
|
|
Массовый расход |
G |
кг/с |
|
|
Мольная доля |
|
моль/моль смеси, % |
|
|
Мольная теплоёмкость |
C |
Дж/(моль×К) |
|
|
Молярная масса |
|
г/моль,кг/кмоль |
|
|
Мощность |
N |
Вт, КВт |
|
|
Объём |
V |
м3 |
|
|
Объёмная доля |
|
м3/м3 смеси, % |
|
|
Объёмная теплоёмкость |
C' |
Дж/нм3×К |
|
|
Объёмный расход |
|
м3/с |
|
|
Площадь сечения |
F |
м2 |
|
|
Показатель адиабаты |
k |
– (безразм.) |
|
|
Показатель политропы |
n |
– (безразм.) |
|
|
Работа |
L, l |
Дж, Дж/кг |
|
|
Скорость потока |
|
м/с |
|
|
Температура |
T, t |
К, °С |
|
|
Теплота парообразования |
r |
Дж/кг |
|
|
Термический КПД |
T |
% |
|
|
Удельный объём |
v |
м3/кг |
|
|
Энергия |
E |
Дж |
|
|
Энтальпия |
H, h |
Дж, Дж/кг |
|
|
Энтропия |
S, s |
Дж/К, Дж/(кг×К) |
|
|
|
|
|
|
|
|
Индексы. |
|
|
Индекс |
Значение |
А |
Абсолютное давление |
ВАК |
Вакуумметрическое давление |
И |
Манометрическое давление |
Индекс |
Значение |
V |
Изохорический процесс |
П |
Политропный процесс |
T |
Изотермический процесс |
- 4 -
www.mitht.ru/e-library
|
|
|
|
|
Изобарический процесс |
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
S |
Адиабатический процесс |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Глава 1. Основные положения технической термодинамики. |
|
|
|
|
|
|||||
|
|
|
|
|
Краткая теоретическая часть. |
|
|
|
|
|
||||
|
|
|
Термодинамика – это наука об энергии – как универсальной |
качест- |
||||||||||
венной и количественной характеристики макроскопических тел, способ- |
||||||||||||||
ных совершать работу и отдавать тепло. |
|
|
|
|
|
|
|
|||||||
|
|
|
Техническая термодинамика изучает закономерности превращения энер- |
|||||||||||
гии в тепловых двигателях и холодильных машинах. Эта наука рассматривает |
||||||||||||||
круг вопросов, связанных с превращением тепловой энергии в работу и обрат- |
||||||||||||||
но, а так же с термомеханической системой (сжатие и расширение газообразно- |
||||||||||||||
го тела, возможности фазового перехода в жидкое состояние). Особое место в |
||||||||||||||
технической термодинамике занимает раздел «Термодинамика потока», изу- |
||||||||||||||
чающий закономерности превращения энергии в потоке сплошной среды. |
||||||||||||||
|
|
|
Химическая термодинамика изучает закономерности превращения энер- |
|||||||||||
гии при изменении химического состава термодинамической системы. |
|
|
|
|
|
|||||||||
|
|
|
Термодинамическая система – это тело или группа тел, находящихся во |
|||||||||||
взаимодействии, мысленно или реально обособленные от окружающей |
среды и |
|||||||||||||
может быть как: гомогенной, гетерогенной, изолированной и др. |
|
|
|
|
|
|||||||||
|
|
|
Термодинамическая система находящаяся в равновесии определяется |
|||||||||||
комплексом независимых термических характеристик, к которым относятся: |
||||||||||||||
температура – К, абсолютное давление – p, Па, и удельный объем – V,м3/кг . |
||||||||||||||
Связь абсолютного давления с манометрическим, вакууметрическим и баро |
|
- |
||||||||||||
метрическим давлениями показана на рис. 1.1. и определяется соотношениями |
||||||||||||||
1.1.-1.2. |
|
Pата = Pати + B; |
|
(1.1) |
|
|||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Pата = B – Pвак, |
|
(1.2) |
|
|
|
||||
|
|
|
где: Pати – избыточное давление, измеряемое по манометру; Pвак – давле- |
|||||||||||
ние, измеряемое по вакуумметру; B – давление, измеряемое по барометру. |
||||||||||||||
|
|
|
Единицы измерения давления: |
|
|
|
|
|
|
|
||||
|
|
в системе СИ: P - Па = Н/м2 (1 Н = 1 кг×м/с2); |
|
|
|
|
|
|
||||||
|
|
|
в внесистемных единицах: - 1 бар = 105 |
Па = 750 ммHg; |
|
|
|
|
|
|||||
|
|
|
в технической системе единиц: 1 техническая атмосфера – 1 ат = 1 кг/см2 = |
|||||||||||
=0,981×105 Па = 735,6 ммHg = 10 мH2O.
Совокупность всех физико-химических свойств системы характеризует её термодинамическое состояние. Все величины, характеризующие какое-либо макроскопическое свойство рассматриваемой системы – параметры состояния.
Опытным путём установлено, что для однозначной характеристики данной системы необходимо использовать некоторое число параметров, называемых независимыми; все остальные параметры рассматриваются как функции не-
зависимых параметров. В качестве независимых параметров состояния обычно выбирают параметры, поддающиеся непосредственному измерению (например, температуру, давление, концентрацию и пр.). Всякое изменение термодинами-
ческого состояния системы (изменение хотя бы одного параметра состояния) есть термодинамический процесс.
- 5 -
www.mitht.ru/e-library
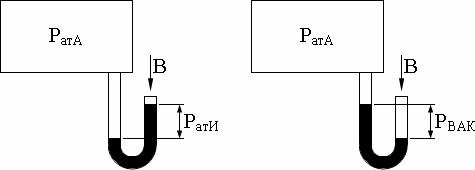
Рис. 1.1.
Измерение давления.
Термодинамическая система находящаяся в равновесии так же определя- |
||||
ется калорическими величинами, к которым относятся: внутренняя энергия, |
||||
энтальпия и энтропия, которые являются функциями состояния системы. |
||||
Внутренняя энергия - это совокупность всех форм энергии, присущих |
||||
данной термодинамической системе. |
|
|||
Энтальпия – это энергия расширенной термодинамической системы, со- |
||||
стоящая собственно из внутренней энергии и работы, которую термодинамиче- |
||||
ская система объемом V должна совершить работу, чтобы вывести ее в окру- |
||||
жающую среду с давлением p. |
h = u + Pv. |
(1.3) |
||
|
||||
Энтропия – универсальная характеристика макроскопических тел, пока- |
||||
зывающая меру ее необратимости. |
|
|
||
Единицы измерения энергии: |
|
|
||
в системе СИ: 1 Дж = 1 Н/м = 1 кг×м2/с2 = Вт×с; |
|
|||
в технической системе единиц: 1 кал. |
|
|||
Переводное соотношение: 1 кал = 4,184 Дж. |
|
|||
Нормальные условия (н.у.): |
|
|
||
давление, равное 1 физической атмосфере Pн = 760 ммHg; |
|
|||
температура, Tн = 273 К. |
|
|
|
|
Каждая термодинамическая система, находящаяся в состоянии равнове- |
||||
сия характеризуется уравнением состояния вида: |
(1.4) |
|||
F(P, V, T) = 0. |
||||
Параметры состояния термодинамической системы должны быть одина- |
||||
ковыми по всему её объёму. В таком случае её состояние вполне определяется |
||||
заданием двух параметров, а третий является их функцией: |
(1.5) |
|||
P = F1(V, T); V = F2(P, T); T = F3(P, V). |
||||
Уравнение состояния идеального газа: |
|
|||
для единичной массы термодинамической системы: |
(1.6) |
|||
|
Pv = RT; |
|||
для массы термодинамической системы: |
(1.7) |
|||
|
PV = MRT. |
|||
Уравнение состояния для реальной термодинамической системы: |
|
|||
P |
a |
v b RT, |
(1.8) |
|
v2 |
||||
|
|
|
||
где: R – универсальная газовая постоянная; a, b – постоянные для каждого газа.
- 6 -
www.mitht.ru/e-library

Задачи для самостоятельной работы.
Задача 1-1. Манометр показывает давление PатИ = 6 кГ/см2 при барометрическом давлении B = 752 ммHg. Каково будет абсолютное давление PатА, если его выразить в Н/м2, бар, кГ/м2, кГ/см2, ммHg, ммH2O? Каково будет показание манометра, выраженное в этих же единицах, при атмосферном давлении B = 0,590 бар, если абсолютное давление останется неизменным? Принять ускорение свободного падения g = 9,807 м/с2, плотность воды ρВ = = 998 кг/м3, плотность ртути ρРТ = 13533,6 кг/м3.
Задача 1-2. В конденсаторах турбины поддерживается абсолютное давление равное PатА1 = 0,03 кГ/см2, PатА2 = 3,807 кН/м2. Определить вакуум в каждом конденсаторе (значение вакуумметрического давления) и выразить его в процентах от барометрического давления B = 753 ммHg.
Задача 1-3. Манометр, установленный на баллоне акваланга, на поверхности водоёма показывает давление равное PатИ = 50 ат. Определить абсолютное давление воздуха в баллоне и показания манометра под водой на глубине 40 м, если барометрическое давление равно B = 1 атм.
Задача 1-4. Микроманометр (см. рис. 1.2), присоединённый к воздуховоду, заполнен спиртом с плотностью ρСП = 800 кг/м3. Определить абсолютное давление в воздухопроводе, если длина столба жидкости в трубке микроманометра, наклонённой под углом α = 30 °, равна 180 мм, а барометрическое давление B = 1,02 бар. Выразить абсолютное давление в бар, ммHg, кГ/см2.
Задача 1-5. Давление в паровом котле PатИ = 0,4 бар при барометрическом давлении B1 = 725 ммHg. Чему будет равно избыточное давление в котле, если показание барометра повысится до B2 = 785 ммHg, а состояние пара в котле останется прежним?
Рис. 1.2.
Микроманометр, присоединённый к воздуховоду.
Задача 1-6. Резервуар объёмом 4 м3 |
заполнен углекислым газом. Опреде- |
||||
лить массу газа, если его избыточное давление равно PатИ = 0,4 бар, а темпера- |
|||||
тура равна t = 80 °С. Давление воздуха по барометру составляет B = 780 ммHg. |
|||||
Задача 1-7. Для пуска двигателя используется сжатый воздух, находя- |
|||||
щийся в ресивере. Показание манометра до пуска двигателя 5,7 МПа. После |
|||||
пуска давление воздуха в баллоне уменьшилось и составляло 2,8 МПа. Опреде- |
|||||
лить отношение давлений в баллоне до и после пуска двигателя при барометри- |
|||||
ческом давлении 1,03 бар. |
|
|
занимает при |
давлении равном |
|
Задача 1-8. Азот массой M = 3,62 кг |
|||||
P = 1 физ. атм. и температуре равной T = 300 К объём V = 3,29 н.м3. Определить |
|||||
газовую постоянную R, полагая PV = MRT. |
нормальных |
условиях |
равна |
||
Задача 1-9. Плотность |
воздуха |
при |
|||
ρ = 1,293 кг/н.м3. Определить |
плотность воздуха при |
давлении |
равном |
||
P = 15 бар и температуре равной t = 20 °С. |
|
|
|
|
|
|
- 7 - |
|
|
|
|
www.mitht.ru/e-library
Пример 1-1. Определить массу 5 м3 водорода при абсолютном давлении равном Pата = 6 бар и температуре равной t = 100 °С.
Решение.
M = PVμ/RT = (6×105 × 5 × 2×10–3)/(8,314) × (100 + 273,15)) = 1,93 кг.
Глава 2. Первое начало термодинамики.
Краткая теоретическая часть.
Первое начало термодинамики является следствием общего закона сохранения энергии и представляет собой постулат, устанавливая соотношение между теплотой Q, работой L и изменением внутренней энергии термодинамической системы и математически может быть выражена соотношениями вида:
U = Q – L; |
(2.1) |
U = δQ – δL. |
(2.2) |
Теплота и работа характеризует качественно и количественно две раз-
ные формы передачи энергии. Они не могут содержаться в термодинамической системе и возникают только при взаимодействии термодинамической системы с окружающей средой.
Теплота есть форма передачи энергии путем неупорядоченного движения микрочастиц термодинамической системы
Работа – направленный процесс, связанный с перемещением ТС, изменением ее параметров
Задачи для самостоятельной работы.
Задача 2-1. 1,5 л воды нагреваются электрическим кипятильником мощностью 300 Вт до температуры кипения. Определить время нагревания τ, если начальная температура воды T1 = 293 К, а теплообмен с окружающей средой отсутствует.
Задача 2-2. В котельной электрической станции за 20 ч работы сожжено 62 тонны каменного угля, имеющего теплоту сгорания 28900 кДж/кг. Определить среднюю мощность станции, если в электрическую энергию превращено 18 % тепла, полученного при сгорании угля.
Задача 2-3. Сколько кг свинца можно нагреть от температуры T1 = 288 К до температуры его плавления TПЛ = 600 К посредством удара молота массой 20 кг при падении его с высоты 2 м? Предполагается, что вся энергия молота превращается в тепло, целиком поглощаемое свинцом. Теплоёмкость свинца равна CP = 0,1256 кДж/(кг×К).
Задача 2-4. На электростанции мощностью N = 100 МВт сжигается топ-
ливо с теплотой сгорания QP = 30000 кДж/кг. КПД станции T = 33,0 %. Определить часовой расход топлива G.
Задача 2-5. воздух в цилиндре занимает объём V1 = 0,25 дм3 и находится под давлением P1 = 1 бар. Объём воздуха при изотермическом расширении становится равным V2 = 1,5 дм3. Определить конечное давление P2 и работу расширения.
Задача 2-6. Жидкость, находящаяся в сосуде и сообщающаяся с атмосферой B = 1 бар в течение τ = 30 мин перемешивается мешалкой с постоянной частотой вращения равной n = 75 мин–1 и крутящим моментом равным M = 12,2 кГм. Начальный объём жидкости равный V1 = 3,4 м3 увеличивается при этом на
- 8 -
www.mitht.ru/e-library
3 %. Определить работу расширения жидкости и работу вращения вала. Результаты сравнить.
Задача 2-7. Паровая турбина расходует 0,00110 кг пара на получение 1 кДж электроэнергии. На производство 1 кг пара необходимых параметров затрачивается 3300 кДж. Определить КПД паротурбинной установки.
Задача 2-8. Определить суточный расход топлива на станции мощностью равной N = 100000 кВт, если её КПД 35 %, а теплота сгорания топлива QP = 30000 кДж/кг. Определить также удельный расход топлива на 1 МДж переработанной энергии.
Задача 2-9. Какова стоимость энергии, необходимой для подъёма 1000 кг оборудования на вершину башни высотой 516 м, если цена электроэнергии со-
ставляет 2 коп/кВт×ч, а КПД подъёмного механизма равен = 0,85?
Пример 2-1. Паросиловая установка мощностью равной N = 4200 кВт
имеет T = 0,33. Определить расход топлива в час, если его теплота сгорания
QP = 25000 кДж/кг.
Решение. G = N/( TQP) = 4200 /(0,33 × 25000) = 1833 кг/ч.
Глава 3. Смеси идеальных газов.
Краткая теоретическая часть.
Газовая смесь – это механическая смесь отдельных газов, не всту- |
|||||||||||||||||||||||||||||||||||||||||
пающих между собой ни в какие химические реакции. Газовая смесь может |
|||||||||||||||||||||||||||||||||||||||||
быть задана массовыми, мольными и объёмными долями: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
m |
i |
|
|
|
|
|
|
|
|
Mi |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
(3.1) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
MСМЕСИ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
σ |
i |
|
|
|
|
|
ξi |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.2) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξСМЕСИ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
τ |
i |
|
|
|
|
|
|
|
|
Vi |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.3) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СМЕСИ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Причём имеют место быть условия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
mi 1; |
|
|
σi 1; τi |
1, |
|
|
|
|
|
|
|
|
|
(3.4) |
||||||||||||||||||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где k – количество газов, составляющих газовую смесь. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Соотношения, связывающие вышеприведённые уравнения: |
|
||||||||||||||||||||||||||||||||||||||||
|
|
m |
i |
VСМЕСИ τ |
i |
|
|
|
|
|
|
|
|
μi |
|
τ |
i |
|
RСМЕСИ |
τ |
; |
|
|
|
|
|
(3.5) |
||||||||||||||
|
|
|
|
μ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
V |
|
|
|
|
|
|
СМЕСИ |
|
|
|
|
|
R |
i |
|
|
i |
|
|
|
|
|
|
|
|||||||||||
|
|
ρСМЕСИ m |
|
i |
Vi |
|
|
|
|
|
|
|
|
|
|
Ri |
|
|
|
μСМЕСИ m |
|
|
|||||||||||||||||||
τ |
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
m |
|
|
|
. |
(3.6) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|||||||||||||||||||||||||
|
i |
ρ |
i |
|
|
i |
|
V |
|
|
|
|
|
|
|
|
|
|
i |
|
СМЕСИ |
|
i |
|
|
|
μ |
i |
|
|
i |
|
|
||||||||
|
|
|
|
|
|
|
|
СМЕСИ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Газовая постоянная смеси газов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
m |
|
|
|
m |
|
|
|
|
1 |
|
|
|
|||||||||
RСМЕСИ miRi 8,314 |
|
1 |
|
|
|
|
|
|
2 ... |
|
|
k |
|
|
|
|
. |
(3.7) |
|||||||||||||||||||||||
|
μ |
|
μ |
|
k |
τ |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
μ |
|
2 |
|
|
k |
|
|
|
|
i |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Средняя молекулярная масса смеси газов: |
|
|
|
|
|
|
|
|
i 1 |
Ri |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
μ |
СМЕСИ |
|
|
8,314 |
|
|
|
|
1 |
|||
m R |
m |
R |
|
... m |
R |
|
k |
m |
||||
|
|
|
|
|
||||||||
|
|
|
1 1 |
2 |
|
2 |
k |
|
k |
|
i 1 μii |
|
Парциальное давление газа: |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
- 9 - |
|
|
|
|
|
k
τiμi. (3.8)
i 1
www.mitht.ru/e-library
P P |
m |
|
Ri |
P |
m |
|
μi |
τ P |
. |
(3.9) |
||
i RСМЕСИ |
i μСМЕСИ |
|||||||||||
i |
СМЕСИ |
|
СМЕСИ |
|
i СМЕСИ |
|
|
|||||
|
Задачи для самостоятельной работы. |
|
|
|||||||||
Задача 3-1.В резервуаре ёмкостью 125 м3 находится коксовый газ при |
||||||||||||
давлении равном P = 5 бар и температуре T = 291 К. Газ имеет следующий объ- |
||||||||||||
ёмный состав: (H2O) = 0,46; (CH4) = 0,32; (CO) = 0,15 и (N2) = 0,07. После |
||||
отбора части газа его давление снизилось до 3 бар, а температура до 285 К. Оп- |
||||
ределить массу израсходованного газа. |
водорода |
и азота |
равна |
|
Задача 3-2. Газовая |
постоянная смеси |
|||
RСМЕСИ = 882,54 Дж/(кг×К). Определить массовые доли водорода и азота, если |
||||
давление смеси PСМЕСИ = 1,08 бар. |
|
|
|
|
Задача 3-3. Поток воздуха, имеющий часовой расход GВ = 300 кг/ч и тем- |
||||
пературу TВ = 573 К, смешивается с потоком дымовых газов GГ = 400 кг/ч, |
||||
TГ = 873 К. Определить температуру смеси и объёмные доли газов, если извест- |
||||
но, что RГ = 289,277 Дж/(кг×К). Принять давление газов и воздуха одинаковы- |
||||
ми, а теплоёмкость газов равной теплоёмкости воздуха. |
|
|
||
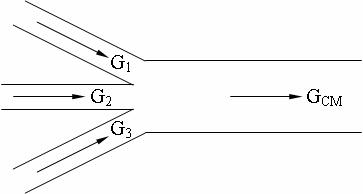
Задача 3-4. Три газовых потока смешиваются между собой (см. рис. 3.1). |
||||
Первый поток представляет |
собой поток кислорода с |
расходом |
равным |
|
G1 = 115 кг/ч и температурой T1 = 573 К, второй – поток оксида углерода (II) с |
||||
расходом равным G2 = 200 кг/ч и температурой T2 |
= 473 К. По третьему каналу |
|||
течёт воздух с температурой T3 = 673 К. В результате смешивания этих потоков образуется смесь с температурой TСМ = 548 К. Определить часовой расход воздуха, если известно, что давление всех трёх газов одинаково.
Рис. 3.1.
Смешение трёх газовых потоков.
Задача 3-5. Смесь, состоящая из 1 киломоль кислорода и двух киломоль азота при температуре равной T1 = 303 К и давлении равном P1 = 1 бар охлаждается при постоянном объёме до температуры T2 = 283 К. Определить изменение внутренней энергии смеси.
Задача 3-6. 0,3 м3 воздуха смешиваются с 0,5 кг углекислого газа. Оба газа до смешивания имели параметры P = 6 бар и T = 318 К. Определить парциальное давление углекислого газа после смешивания.
Задача 3-7. Объёмный состав горючего газа следующий: τ(CO) = 10 %;
τ(N2) = 45 %; τ(CH4) = 35 %; τ(C2H4) = 4 %; τ(H2) = 3 % и τ(CO2) = 3 %. Опреде-
лить кажущуюся молекулярную массу, плотность, удельный объём при н. у., газовую постоянную R и парциальное давление метана в процентах, а также массовую долю каждого компонента.
Задача 3-8. Смесь газов состоит из 10 кг азота, 13 кг аргона и 27 кг диоксида углерода. Определить мольный состав смеси, её удельный объём при н. у.,
- 10 -
www.mitht.ru/e-library
