Семинар №7

Структура данных RиT:

n=n1+n2

Итерационный алгоритм улучшения начального разрезания гиперграфа схемы.

1. S:=S₀; R:=1..n₁; T:=1..n₂

2. ∀xi∈X’:

   1. ∀xj∈X\X’:

      1. Ui:=Гxi, Uj:=Гxj, ΔS(x_i)⁺:=ΔS(x_i)^-:=ΔS(x_j)⁺:=ΔS(x_j)^-:=0

      2. ∀Uk∈Ui:

         1. Xk:=ГUk

         2. (Xk\Xi) ⋂(X’Xj) ≠0 ⇒ п.2.1.2.4

         3. ΔS(x_i)^-:= ΔS(x_i)^-+1⇒ п.2.1.2.6

         4. Xk ⋂(X\X’) ≠0 ⇒ п.2.1.2.6

         5. ΔS(x_i)⁺:= ΔS(x_i)⁺+1

         6. Конец цикла

      3. ∀Ul∈Uj:

         1. Xl:=ГUl

         2. (Xl\Xj) ⋂((X\X’)Xi) ≠0 ⇒ п.2.1.3.4

         3. ΔS(x_j)^-:= ΔS(x_j)^-+1⇒ п.2.1.3.6

         4. Xl ⋂X’ ≠0 ⇒ п.2.1.3.6

         5. ΔS(x_j)⁺:= ΔS(x_j)⁺+1

         6. Конец цикла

      4. S_i,j:= (ΔS(x_i)^-+ΔS(x_j)^-)-(ΔS(x_i)⁺+ΔS(x_j)⁺).

      5. Конец цикла

   2. Конец цикла

3. S_p,q:=max{S_i,j∈S}

4. S_p,q ≤ 0 ⇒ п.6

5. Перестановка Xp∈X’ и Xq∈X\X’⇒ п.2

6. Конец работы алгоритма.

Оценка вычислительной сложности:

|X’|=|X\X’|=n/2;

|Гx_i|=|Гx_j|=A;

|x_k|=|x_l|=;

П.2.1.2 = A;

П.2.1.3 = A;

П.3 = двойной цикл |S_i,j|-1=

На i-ой итерации:

N_f=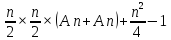=O();

Итоговая вычислительная сложность:

O()-(n-a)=O();

Семинар №8

16. Обдумайте, необходимо ли после перестановки вершин x_pиx_qзаново пересчитывать показательSдля всех парных обменов. Как определить вершины, для парных обменов которых необходимо пересчитыватьS? Доработайте алгоритм так, чтобы после очередного обмена пересчитыватьSдля парных обменов только таких вершин.

После перестановки XpиXqнет необходимости пересчитывать показательSдля вершин, не смежныхXpиXqи составляющих парный обмен.

H_l

H\H_l

Пусть Xp:=Г₁(X_p), Xq:=Г₁(X_q), Xpq:= X_p ∪ X_q, Xpq’:= X_pq ⋂ X₁’, Xpq’’:= X_pq\X_pq’.

Тогда пересчет S:

∀xi∈ X’: ∀xj∈ X\X’: xi∈ X_pq’∪ xj∈ X_pq’’

17. Выполните улучшение итерационным алгоритмом полученного Вами разрезания гиперграфа схемы. Сравните результаты разбиения гиперграфа схемы последовательным и итерационным алгоритмами. Сделайте заключение о вычислительной сложности этих алгоритмов.

Улучшенный итерационный алгоритм улучшения начального разрезания гиперграфа схемы.

1. S:=S₀; R:=1..n₁; T:=1..n₂, Xpq’:=X’, Xpq’’:=X\X’, Xpq:=X

2. ∀xi∈X’:

   1. ∀xj∈X\X’:

      1. xi∈ Xpq’ ∪ xj∈ Xpq’’ ⇒ п.2.1.3

      2. ⇒ п.2.1.7

      3. Ui:=Гxi, Uj:=Гxj, ΔS(x_i)⁺:=ΔS(x_i)^-:=ΔS(x_j)⁺:=ΔS(x_j)^-:=0

      4. ∀Uk∈Ui:

         1. Xk:=ГUk

         2. (Xk\Xi) ⋂(X’Xj) ≠0 ⇒ п.2.1.4.4

         3. ΔS(x_i)^-:= ΔS(x_i)^-+1⇒ п.2.1.4.6

         4. Xk ⋂(X\X’) ≠0 ⇒ п.2.1.4.6

         5. ΔS(x_i)⁺:= ΔS(x_i)⁺+1

         6. Конец цикла

      5. ∀Ul∈Uj:

         1. Xl:=ГUl

         2. (Xl\Xj) ⋂((X\X’)Xi) ≠0 ⇒ п.2.1.3.4

         3. ΔS(x_j)^-:= ΔS(x_j)^-+1⇒ п.2.1.3.6

         4. Xl ⋂X’ ≠0 ⇒ п.2.1.3.6

         5. ΔS(x_j)⁺:= ΔS(x_j)⁺+1

         6. Конец цикла

      6. S_i,j:= (ΔS(x_i)^-+ΔS(x_j)^-)-(ΔS(x_i)⁺+ΔS(x_j)⁺).

      7. Конец цикла

   2. Конец цикла

3. S_p,q:=max{S_i,j∈S}

4. S_p,q ≤ 0 ⇒ п.8

5. Перестановка Xp∈X’ и Xq∈X\X’

6. Xpq:=F₁(Xp)∪F₁(Xq)

7. Xpq’:=Xpq⋂X’,Xpq’’:=Xpq\Xpq’ ⇒ п.2

8. Конец работы алгоритма.

Оценка вычислительной сложности:

|X’|=|X\X’|=n/2;|Гx_i|=|Гx_j|=A;|ГU_k|=|ГU_l|=;|X’pq|= A;| X’\X’pq|=A;|X’’pq|= A;|x_k|=|x_l|=;

П.2.1.4 = A;П.2.1.5 = A;П.5 = двойной цикл | S_i,j|-1=

На i-ой итерации:

N_f = =O();

Итоговая вычислительная сложность:

O()-(n-a)=O();

Вычислительная сложность итерационного алгоритма улучшения начального разрезания гиперграфа схемы больше вычислительной сложности алгоритма последовательного разрезания гиперграфа:

O()> O();