Семинар №4

13. Доработайте основные пункты алгоритма последовательного разрезания гиперграфа, используя полученные вами выражения.

 := - Определение.

∀ - Квантор всеобщности.

K_l- число внешних выводовl-ой части схемы, т.е. ограничение на число выводов.

n_l- число элементовl-ой части схемы, т.е. требуемое число элементов.

Алгоритм последовательного разрезания гиперграфа:

1. Xl:={Xq}, где S(Xq)=max(Si, Si∈S) //Выбор начальной вершины с max числом ребер, попадающих в разрез.

2. U’:= Г(Xl) // множество U' ребер, содержащих вершины множества Xl

3. X’:= Г(U’) // множество X' вершин, инцидентных ребрам множества U'

4. X’’:=X’\Xl // множество Х'' вершин-кандидатов на включение в Xl

∀xi∈X’’: Si:= |Г(XlXi)⋂Г(X\{XlXi})| //Построение множества чисел ребер, попадающих в разрез.

5. X_t ⇔S_t:=min(Si,Si∈S) //Выбор вершины сminчислом ребер, попадающих в разрез.

6. S_t­>K_l ⇒ п.9 //Случай нарушения ограничения на число выводов.

7. Xl:=XlXt//Добавляем новую вершину к множествуXl.

8. | Xl|<n_l⇒ п.2 //Случай неполного набора требуемого числа элементов.

9. Xl – сформировано. ⇒ п.11

10. Формирование множества невозможно.

11. Конец работы алгоритма.

Оценка вычислительной сложности:

| X_l| = |X\X_l|=n/2;

|Гx_i|=;

В процессе получения U’ его мощность увеличивается на |Гx_j|=. Так как

| X_l| = |X\X_l|=n/2, то для Г(X_l):

K===

Для всех Г(X_l) и Г(X\X_l):

K=

Среднее число ребер оценим из :

m_ср=

Для определения U₁ ⋂U₂требуется:

Сложность на i-том шаге:

F=, так что:

F=O(n­²)

Подсчет Sидетn-1 раз, так что:

F=O(n­²)O(n­)=O(n­³)

Семинар №5

14. «...» проанализируйте возможные состояния ребер, инцидентных вершине x_t , сформулируйте условия, выполнение которых определяет ребра, уходящие из разреза и появляющиеся в нем после включения вX_lвершиныx_t.

1. Ребра приходящие в разрез:

U_t∈ГX_t

ГU_t ⋂X_l=∅ ⇒ ΔS_t⁺:= ΔS_t⁺+1

2. Ребра уходящие из разреза:

∀U_t ∈ГX_t:

X_t= ГU_t

X_t \ (X_t ⊂X_l)⇒ ΔS_t^-:= ΔS_t^-+1

ΔS_t:= ΔS_t⁺-ΔS_t^-

15. Доработайте описанный выше алгоритм таким образом, чтобы после включения вершины x_tв подмножествоX_lмножестваU' илиX'' не определялось заново, а корректировались с использованием сформулированных Вами условий. Предложите рекуррентную формулу для подсчета показателяS(X_lx_i), используя сформулированные Вами условия. Оцените вычислительную сложность ее реализации. Выберите структуры исходных данных и промежуточных результатов.

⊆ - «является подмножеством».

Определим вершины-кандидаты, на включение в X_l на первом шаге:

X_k=F₁x_q

Далее, новые вершины:

X’_k=F₁x_t\x_l

Показатель ΔS_i имеет смысл пересчитывать только для вершин, смежных с X_t:

ΔS_i:= ΔS_i⁺-ΔS_i^-; S_i:= S_i-1+ΔS_i

Для ΔS_i выберем следующую структуру данных:

INT– таблица прямого доступа к векторуR.

Удаление заменим замещением последним элементом вектора R.

Семинар №6

Улучшенный алгоритм последовательного разрезания гиперграфа:

1. Xl:={Xq} //Выбор начальной вершины.

2. S:= |ГXq| //Число ребер инцидентныхXq, т.е. изначально находящихся в разрезе.

3. X_k:=F₁Xq//Множество смежных вершин-кандидатов.

4. ∀xi∈X_k:

   1. ΔS_i⁺:=ΔS_i^-:=0 //Обнуляем счетчики.

   2. U_i:=ГX_i //Ребра, инцидентныеXi.

   3. ∀Uj∈Ui:

      1. X_j:=ГU_j//Вершины, смежныеU_j.

      2. X_j\X_i⊆X_l⇒ ΔS_t^-:= ΔS_t^-+1//Если остальные вершины этого ребра входят вXl– ребро уйдет из разреза.

      3. X_j ⋂X_l=∅⇒ ΔS_t⁺:= ΔS_t⁺+1 //Если ни одна из вершин X_j не находится в X_l – ребро попадает в разрез.

   4. ΔS_i:= ΔS_i⁺-ΔS_i^-//Конечное число ребер,попадающих в разрез.

5. X_t ⇔ΔS_t:=min(ΔSi∈S) //Выберем вершину, которая влечет за собой наименьшее число ребер, попадающих в разрез.

6. S:=S+ ΔS_t//Изменим число разрезаемых ребер.

7. S_­>K_l ⇒ п.14 //Случай нарушения ограничения на число выводов.

8. Xl:=XlXt//Добавляем новую вершину к множествуXl.

9. | Xl|=n_l⇒ п.15 //Случай полного набора требуемого числа элементов.

10. Xk:=Xk\Xt//Удаляем добавленную вершину из множества кандидатов.

11. S:=S\ ΔS_t

12. Xk:=F₁Xt\Xl//Определяем новое множество кандидатов из смежныхX_t, не входящих вXl

13. ⇒ п.4

14. Ограничение по числу внешних выводов. ⇒ п.16

15. Xl – сформировано.

16. Конец работы алгоритма.

Оценка вычислительной сложности:

|x_k|=;

|U_i |=|Гx_i|=;

|X_j|=|ГU_j|=;

| X_l| = I, I=1..n_l;

X_j\X_i⊆X_l– двойной цикл –AI;

По закону Рента:

|R|=A;

Xk:=F₁Xt\Xl - A;

N_f = 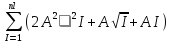=O();

Если для X_lсделать характеристический вектор, то:

N_f’ = =O();

Если вектор Rпредставить в виде двоичной кучи и использовать алгоритм сортировки с вычислительной сложностьюO(n), то вычислительная сложность будетO(n).