Московский ордена Ленина, ордена Октябрьской революции и

ордена Трудового Красного Знамени государственный

технический университет им. Н. Э. Баумана

"УТВЕРЖДАЮ"

Заведующий кафедрой ИУ-6

д. т. н., профессор

_____________ Сюзев В.В.

ОТЧЕТ

ПО ПРОВЕДЕНИЮ ПРАКТИЧЕСКОГО ЗАНЯТИЯ

"РАЗРАБОТКА И ИССЛЕДОВАНИЕ ПОСЛЕДОВАТЕЛЬНОГО И ИТЕРАЦИОННОГО АЛГОРИТМОВ КОМПОНОВКИ СХЕМ ЭВМ"

Составил: ст.гр.ИУ6-93 Красовский М.С

Руководитель: д. т. н., профессор Овчинников В.A.

Москва 2010 г.

ЦЕЛЬЮ ПРАКТИЧЕСКОГО ЗАНЯТИЯ является изучение, модификация и сравнительная оценка последовательного и итерационного алгоритмов компоновки схем ЭВМ.

Условные обозначения:

Поставленный вопрос

Ответ на поставленный вопрос

Теоретическая выкладка

Алгоритм

Семинар №1

1. Сформулируйте условие, проверяющее по гиперграфу схемы принадлежность элементов Э_iи Э_kцепи C_j.

Гиперграф можно определить как два непересекающихся множества X – вершин и U – ребер, на элементах которых задана пара двуместных предикатов-отношений инцидентности Г1(X,U) и Г2(U,X). Предикат Г1(X,U) соответствует такой связи между элементами множеств X и U, которая содержательно определяется выражением – «вершинам множества X инцидентны ребра множества U», а предикат Г2(U,X) можно записать как «ребрам множества U инцидентны вершины множества X».

∈ - Принадлежность к множеству.

∧ - Конъюнкция («и»).

{ , } - Множество элементов.

⊆ - «является подмножеством».

x_iГ₂u_j ∧x_kГ₂u_j

или

{ x_i ,x_k} ⊆Г₂u_j

или

x_i ,x_k Г₂u_j

2. Раскройте смысл выражения Г2u_jГ2u_l, j, lM=1,m и обсудите возможность его справедливости для подмножеств вершин гиперграфа, представляющих цепи схемы.

 - Пересечение.

 - Неравенство.

 - Пустое множество.

Для некоторой пары ребер u_jиu_l присутствует хотя бы одна общая вершина, инцендентная им одновременно. Данное условие проверяет связность гиперграфа.

3. Докажите, что при представлении схемы гиперграфом учитывается фактор неизвестности соединения.

Г₂u_j – множество элементов, соединенных цепьюu_j.

Множество – совокупность неупорядоченных элементов.

При работе с множествами учитывается фактор неизвестности соединения. Описание цепи не диктует порядок соединения этой цепи.

4. Используя «...» способы перехода от схемы к гиперграфу и неориентированному мультиграфу, получите геометрическое задание этих математических моделей схемы «...».

Граф Кёнига - двудольный граф.

Исходная схема:

Гиперграф в виде графа Кёнига:

Формальное описание графа Кёнига на языке описания графов DOT:

dot graph -Tpng -o graph.png -Gsplines=line

graph new {

levels=2;

ranksep=2;

node[shape=plaintext,fontsize=12];

subgraph one {

rank = same;

edge[color=white];

X1--X2--X3--X4--X5--X6--X7--X8--X9--X10--X11--X12;

}

subgraph two {

rank = same;

edge[color=white];

U1--U2--U3--U4--U5--U6--U7--U8--U9--U10--U11;

}

X1:s--U1:n;

X2:s--U2:n;

X3:s--U3:n;X3:s--U4:n;

X4:s--U5:n;X4:s--U6:n;

X5:s--U1:n;X5:s--U3:n;X5:s--U4:n;X5:s--U7:n;

X6:s--U1:n;X6:s--U3:n;X6:s--U5:n;X6:s--U8:n;X6:s--U10:n;

X7:s--U2:n;X7:s--U3:n;X7:s--U9:n;X7:s--U10:n;

X8:s--U2:n;X8:s--U8:n;X8:s--U11:n;

X9:s--U9:n;

X10:s--U10:n;

X11:s--U6:n;X11:s--U9:n;X11:s--U11:n;

X12:s--U7:n;X12:s--U9:n;X12:s--U11:n;

}

Неориентированный мультиграф:

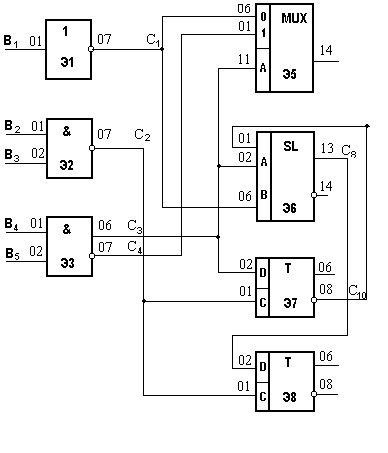
Анализируемая часть схемы:

Построение неориентированного мультиграфа:

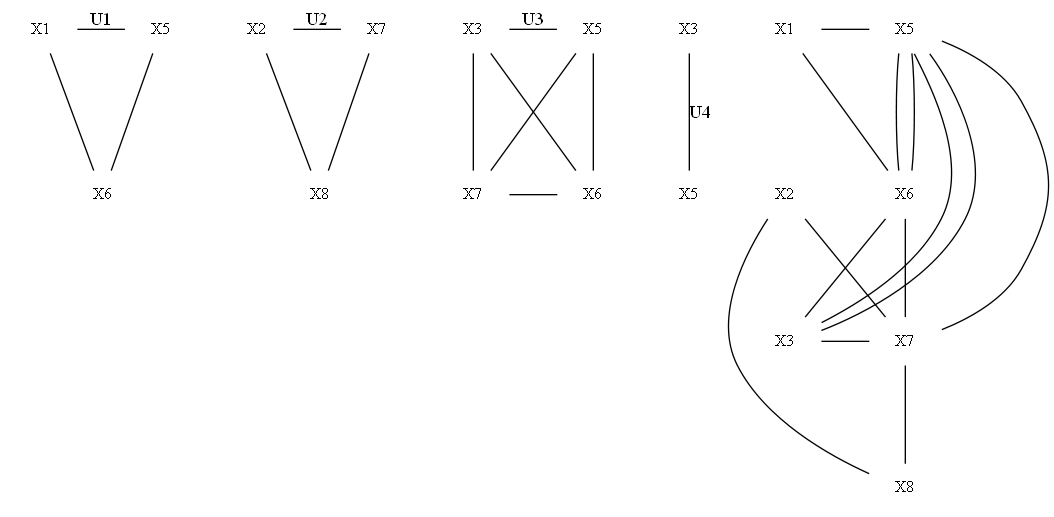
Формальное описание неориентированного мультиграфа на языке описания графов DOT:

graph new {

ranksep=1;

node[shape=plaintext,fontsize=12];

subgraph one {

subgraph n1 {

rank=same;

Xn1[label="X1"];Xn5[label="X5"];

}

subgraph n2 {

rank=same;

Xn6[label="X6"];

}

Xn1--Xn5[label="U1"];

Xn5--Xn6;

Xn6--Xn1;

}

subgraph two {

subgraph w1 {

rank=same;

Xw2[label="X2"];Xw7[label="X7"];

}

subgraph w2 {

rank=same;

Xw8[label="X8"];

}

Xw2--Xw7[label="U2"];

Xw7--Xw8;

Xw8--Xw2;

}

subgraph three {

subgraph h1 {

rank=same;

Xh3[label="X3"];Xh5[label="X5"];

}

subgraph h2 {

rank=same;

Xh6[label="X6"];Xh7[label="X7"];

}

Xh3--Xh5[label="U3"];Xh3--Xh7;Xh3--Xh6;

Xh5--Xh6;Xh5--Xh7;

Xh7--Xh6;

}

subgraph four {

Xo3[label="X3"];Xo5[label="X5"];

Xo3--Xo5[label="U4"];

}

subgraph main {

subgraph m1 {

rank=same;

X1;X5;

}

subgraph m2 {

rank=same;

X2;X6;

}

subgraph m3 {

rank=same;

X3;X7;

}

subgraph m4 {

rank=same;

X8;

}

subgraph m5 {

edge[color=white,weight=100];

X1--X2--X3;

}

subgraph m6 {

edge[weight=100];

X5--X6--X7--X8;

}

X1--X5;X1--X6;

X5--X6;X5--X7;

X2--X7;X2--X8;

X3--X5;X3--X5;X3--X6;X3--X7;

}

}

5. Сделайте вывод о возможности правильной оценки по гиперграфу и неориентированному мультиграфу числа электрических связей между элементами или частями схемы, если между ними имеется хотя бы одна цепь,которая соединяет более двух элементов. Докажите вывод теоретически.

⇔ - Равносильность.

⇒ - Импликация, следование.

| | - Мощность множества.

G(X,U) – Мультиграф.

С помощью гиперграфа можно правильно оценить число электрических связей между элементами, так как взаимооднозначно определены элементы Э и вершины X, связи С и цепиU.

С помощью неориентированного мультиграфа невозможно правильно оценить число электрических связей между элементами, если между ними есть хотя бы одна цепь, которая соединяет более двух элементов, так как нет взаимооднозначного определения связей и цепей в таком представлении.

Доказательство для гипергафа:

Если Э⇔X, C⇔U, то С_i,j⇔ U_i,j ⇒|C|=|U|,| С_i,j |=| U_i,j |.

Доказательство для неориентированного мультиграфа:

Если Э⇔X, C⇒U, то С_i,j⇒ U_i,j ⇒|C|≤|U|, |С_i,j|≤|U_i,j|, если есть цепи, соединяющие более двух элементов.

Таким образом, нельзя правильно оценить число электрических связей.