9. Стратегии декомпозиции пространства решений.
Большинство методов решения комбинационно-оптимизационных задач использует 2 идеи:
Декомпозиция пр-ва решений на некоторые подм-ва.
Выбор перспективного подм-ва на основе некоторой оценки
Существуют две стратегии декомпозиции мн-ва решений: в ширину и в глубину с возвращением.
Процесс декомпозиции: пусть М мн-во вариантов решений некоторой комбинаторной задачи. Декомпозиция этого мн-ва заключается в том, что в соответствии с некоторыми принципом это мн-во разбивается на подм-ва Мiтакие, чтоUMi=M. В общем случаеMiмогут пересекаться, но как правило они не пересекаются. Далее используя тот же принцип полученные подм-ва разбиваются на подм-ва с меньшим кол-вом вариантов и так до тех пор, пока каждое подм-во не будет содержать по 1 варианту. Порядок разбиения подм-в м.б. заданным или вычисленным. Сопоставим каждое подмножество некоторой вершине графа, и, сопоставим вершиныMiиMj, еслиMjполучено непосредственным разбиениемMi. Т.о. получаемдерево декомпозиции(дерево поиска). Принцип разбиения мн-ва решений определяется теми преобразованиями, кот. необходимо выполнить над моделью исходного описания для получения модели рез-та.( т.е. теми преобразованиями, которые необходимо выполнить над исходным графом для получения графа-результата.)
М
етод
декомпозиции в ширину: рассмотрим на
# задачи поиска всех маршрутов, т.е.
простых цепей некоторого графа,
соединяющие 2 заданые вершиныxiиxj. Простая цепь – это
такая последовательность ребер, в
которой ни одно ребро или вершина не
встречаются дважды.
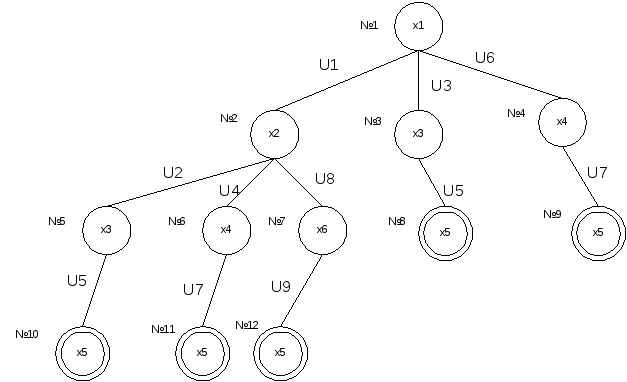
Принцип формирования маршрута – последовательное включ. в простую цепь ребер в порядке возрастания их номеров. принцип разбиения в данном случае вытекает из процедуры формирования маршрута указанного выше. Зададим следующий порядок разбиения подм-в: переход с одного уровня дерева декомпозиций к другому будем осуществлять только после включения в строящиеся цепи текущего ребра. Сопоставим корню дерева решений все мн-во решений: для наглядности этой вершине припишем x1. Данный метод декомпозиции обеспечивает получение всех вариантов решений.
Стратегия декомпозиции в глубину с возвращением:эта стратегия обеспечивает получение всех вариантов решения, но приводит к др. порядку появления этих решений. Заключ. эта стратегия в следующем: на 1-ом шаге мн-во М разбивается на 2 подм-ва М1 и М\М1, далее М1 разбивается на М2 и М1\М2 и т.д. пока подмножество не будет содержать 1 вариант. Затем выполняется возвращение к ближайшему подм-ву, содержащему > 1 варианта. Процедура применяется к этому подмножеству и она применяется до тех пор, пока не будет получено подмн-во всех вариантов.
10. Отсечение и выбор перспективной вершины дерева решений. Верхняя и нижняя границы целевой функции. Пример.
Поиск оптимального решения полным перебором при декомпозиции в ширину или в глубину с возвращением, как правило, нереализуем для задач с размерностью входа более 5-6.
Существование некоторой оценки, которая с той или иной степенью достоверности позволит судить, содержит ли данное подмножество оптимальное решение, позволило бы избежать полного перебора вариантов.
Обозначим такую оценку F(Mi). Очевидно, что для конечного дерева решений эта оценка должна быть равна значению целевой функции для соответствующего решения. В задачах на минимумF(Mi) – это так называемая нижняя граница функцииFдля вариантов, входящих во множествоMi, причем функцияFнеобязательно является целевой функцией, но в любом случае связана с ней. Для задач на максимумF(Mi) – верхняя граница.
Нижняя и верхняя граница означают, что значение целевой функции для всех вариантов, порожденных множеством Mi, не меньше (не больше) числаF(Mi).