35.Метод параллельного поиска

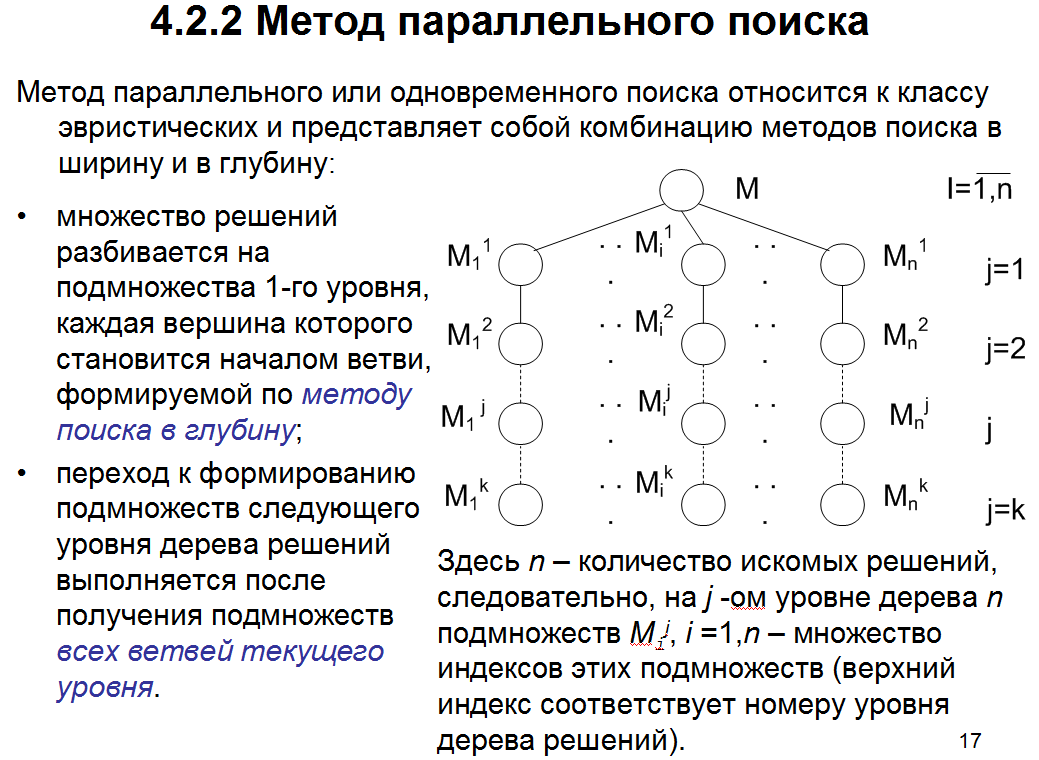
В зависимости от специфики задачи подмножества разных ветвей могут быть как пересекающимися, так и непересекающимися.

Рассмотрим задачу компоновки схемы в nконструктивных модулей. Множество элементов схемыЭ поставлено во взаимнооднозначное соответствие множеству вершинХгиперграфаЭ Х.

Указанная задача может быть решена алгоритмом, реализующим метод параллельного поиска. Результатом его работы будет разбиение множества Хвершин гиперграфа наnподмножествXi,i=1,n. Так как один и тот же элемент схемы не может входить в разные конструктивные модули и составXiопределяется по методу поиска в глубину последовательным включением вершинxXвXji(XjiсоответствуетMji), тоXjiX jp=для всехi, pI ={1,n}. Таким образом, в данной задаче подмножества, принадлежащие разным ветвям дерева решений, должны быть непересекающимися.

Если подмножества вариантов 1-го уровня содержат все варианты решения, т.е. удовлетворяют условию M1i=Mи оценка выбора подмножества в каждой ветви является отсекающей, то метод обеспечивает получение точного решения.

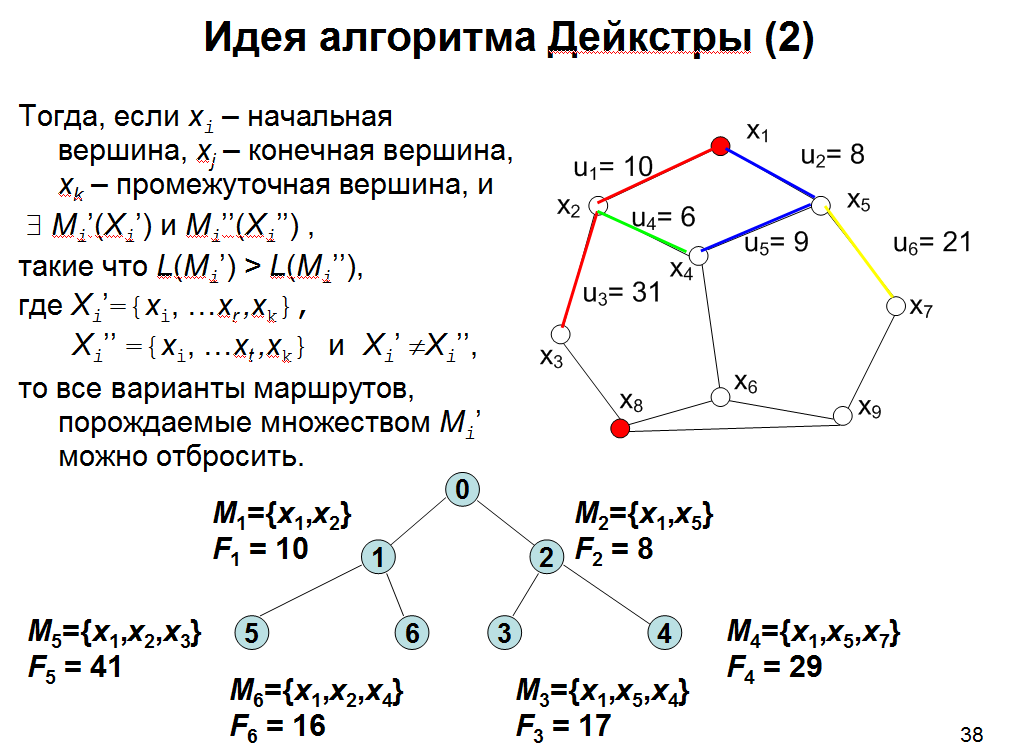
36.Дополнительные отсечения при использовании метода ветвей и границ. Идея алгоритма Дейкстры

Задача: поиск маршрута (простой цепи) минимальной длины из некоторой исходной точки в заданную конечную.

Стратегия декомпозиции множества решений – по методу в ширину.

Принцип разбиения – включение во фрагмент пути некоторого ребра.

Оценочная функция в каждой вершине дерева – суммарная длина ребер уже построенного фрагмента маршрута – нижняя граница целевой функции.

Поскольку гарантия, что эта оценка является отсекающей отсутствует, она может использоваться как оценка перспективности, т. е. для выбора очередной вершины ветвления.

Однако в данном случае эта оценка может выступать в качестве отсекающей в «особых» вершинах дерева решений.

Этот факт основывается на свойстве графа – результата решения:

маршруты, как простые цепи, могут проходить через одну и ту же вершину графа и иметь разную длину до этой вершины.

37.Модификация метода на примере задачи построения гамильтонова цикла с минимальной суммой весов ребер

Основная идея последовательного алгоритма решения задачи коммивояжера по методу поиска в глубину: начиная с заданной исходной вершины из ребер, инцидентных ей, а в дальнейшем – последней вершине фрагмента тура, выбираем то, которое имеет минимальный вес и не образует цикла с уже включенными ребрами, до тех пор, пока количество включенных в тур вершин меньше их числа в графе.

Анализируя процесс преобразования исходного графа в граф результата, мы приходим к выводу, что выбор ребер с малым весом на начальных этапах построения тура может привести к выбору ребер с большим весом на конечных из-за того, что ребра меньшего веса будут образовывать частичные циклы. Т.е. локальный критерий выбора не является отсекающей оценкой, а алгоритм, реализующий поиск в глубину, не строит плана вперед – текущий выбор делается без учета того, к чему это приведет в последующем.

Следовательно для увеличения точности необходимо увеличить глубину просмотра, т.е. выбирать, например, пару ребер с минимальным суммарным весом, одно из ребер которой инцидентно концевой вершине, а другое – смежно этому ребру. При увеличении глубины просмотраkдоk=n, гдеn– количество вершин графа, получим дерево полного перебора.

Данный метод является комбинацией методов поиска в глубину и в ширинус ограничением в видеkна количество уровней при генерации поддерева в ширину. Алгоритм, реализующий эту идею, можно назватьалгоритмом с просмотром на k шагов вперед.

Кроме этого, так как гамильтонов цикл проходит через все вершины:

• можно начинать построение тура с любого ребра;

• целесообразно обеспечить выбор среди ребер, инцидентных обеим концевым вершинам построенного фрагмента тура, (например, для предыдущего графа это обеспечит получение точного решения).

Точное решение l = 10

Выполненный анализ позволил нам сформулировать идею алгоритма, основанного на комбинации метода поиска в глубину и в ширину и указанных выше эвристик:

• из всех пар смежных ребер выбираем ту, которая имеет минимальный вес;

• затем, до тех пор, пока количество вершин, включенных в строящийся тур меньше n-2 (для четного) илиn-1 (для нечетного числа вершин исходного графа), выбираем из всех пар ребер, одно из которых инцидентно той или иной концевой вершине, а второе – смежно этому ребру, ту пару, которая имеет минимальный вес и не образует цикла с уже включенными ребрами.

Алгоритм, реализующий эту идею, является эвристическим, имеет вычислительную сложностьO(n3), для него характерна более высокая вероятность нахождения точного решения, чем по методу поиска в глубину.