26. Последовательный алгоритм разрезания гиперграфа схемы.

Введение.

Разрезаем гиперграф, то есть, разбиваем множество его вершин на 2 (в частном случае) подмножества:и. Формируем, перетаскивая по одной вершине кандидату множества. При этом число рёбер в разрезе должно быть минимальным. Для каждой вершины-кандидата определяем, сколько рёбер попадут в разрез, а сколько – исчезнут из негопри выборе данной вершине. Вычисляетсяи выбирается вершина, для которойминимально. Значениядля всех вершин кандидатов хранятся в массиве.

Выбор структур данных.

В качестве структур данных для аналитического представления гиперграфа будем использовать массивы динамических векторов, так как над ними выполняются только операции доступа. При работе алгоритма будут формироваться и использоваться массивы.

Над массивом мы будем выполнять следующие действия: последовательная выборка элементов, добавление выбранной вершиныв конец массива. Таким образом, структура данных для- динамический вектор. В массивбудем добавлять новые вершины-кандидаты и исключать из него вершину. Для массивацелесообразно использовать одно- или двусвязный список. Над массивомбудут выполняться только операции просмотра его элементов (последовательного доступа), так как его элементы после корректировкипересчитываются заново. Следовательно, структура данных массива- динамический вектор.

Основные пункты одного из вариантов алгоритма.

1. Включаем в формируемое множество некоторую вершину:

2. Определяем количество рёбер 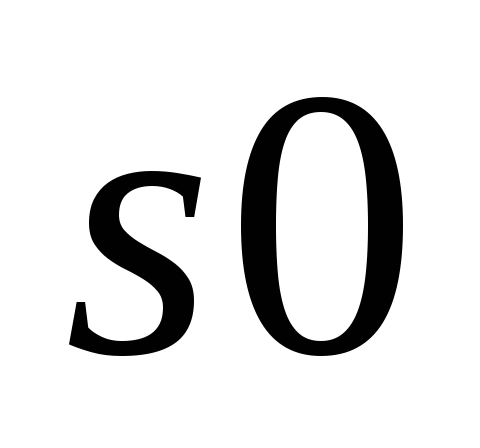, соединяющихс:

3. Находим множество вершин - кандидатов на включение в:

, где

4. Для каждой вершины определяем множество инцидентных ей рёбер, подмножестворёбер, приходящих в разрез, и подсчитываем показатель. Для этого:

4.1.

4.2. для выполняем:

4.2.1. Находим множество вершин , входящих в ребро

4.2.2. Проверяем условие

Если условие не выполняется (ребро остаётся в разрезе) переходим к пп. 4.2.4. Выполнение условия означает, что ребро уходит из разреза – переходим к пп. 4.2.3.

0. Подсчитываем показатель и переходим к п. 4.2.

0. Проверяем условие

Если условие выполняется (ребро приходит в разрез при включенииxi вXl), переходим к пп. 4.2.5. При невыполнении условия переходим к анализу следующего ребра, т.е. к п.

4.2.

4.2.5. Включаем ребро в множество:

,

подсчитываем показатель :

и возвращаемся к п. 4.2.

4.3. Определяем значение :

и заносим его значение в массив :

5. Находим вершину , для которойминимально:

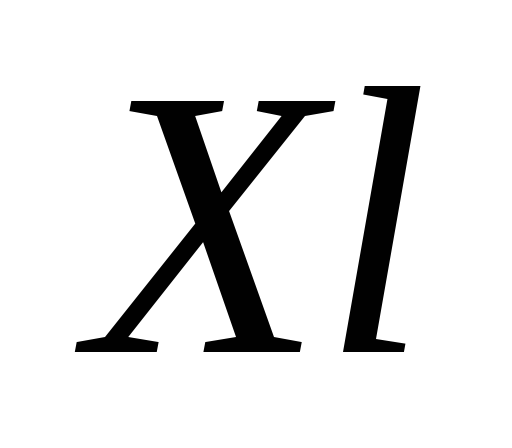6. Подсчитываем количество рёбер , соединяющих множества ипосле включенияв:

7. Проверяем ограничение на количество внешних выводов l-й части схемы:

Если условие выполняется, то переходим к п. 8, иначе – к п. 12.

8. Включаем вершину в множество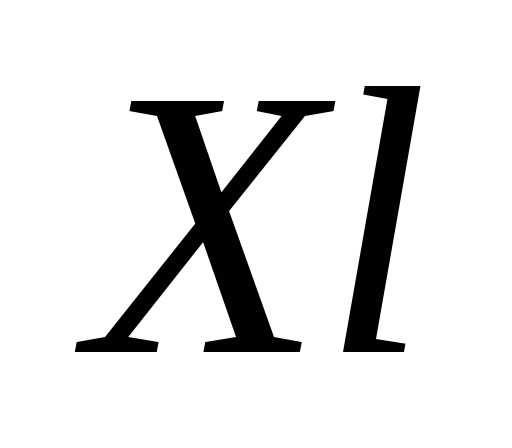и исключаем её из:

9. Проверяем условие:

, гдеnl – требуемое количество элементов вl-й части схемы.Если условие выполняется, то переходим к п.10, иначе – к п.13.

10. Определяем множество вершин, входящих в множество рёбер :

11. Корректируем множество вершин кандидатов :

и возвращаемся к п. 4.

11. Дальнейшее формирование невозможно из-за нарушения ограничения на число внешних выводов. Переход на окончание работы алгоритма к п. 14.

11. Вывод результатов.

11. Конец работы алгоритма.

Вычислительная сложность алгоритма.

Рассмотренный вариант алгоритма имеет . Его можно усовершенствовать, так чтобудет равно.