Эпр диполя Герца

ЭПР отражателей, имеющих длину l, много меньшую длины волны λ (диполь Герца), в десятки раз меньше ЭПР полуволнового отражателя. Количественно ЭПР диполя Герца (σ_l) может быть определена по рассмотренной ранее схеме (см. (5.1.3), (5.1.5), (5.1.8)), с соответствующей заменой σ₁ на σ_l, h_д на l, G₁ на G_l:

; ;

.

Здесь: E – напряженность падающего на диполь электрического поля. Вектор падающего поля предполагается коллинеарным с диполем;

z ‑ комплексное входное сопротивление диполя;

W ‑ волновое сопротивление диполя.

По условиям

У диполя Герца W = 1000 ом [64], коэффициент направленного действия G_l = 1,5. Соответственно максимальное значение ЭПР диполя Герца определяется выражением

, (5.1.24)

что соответствует результатам, полученным Релеем, при исследовании рассеяния волн малыми телами.

Чтобы оценить порядок σ_l, предположим, что l/λ = 0,1, тогда σ_l = 1,8∙10^-3l² м.²

Если l = 0,01 м. то σ_l = 1,8 10^-7 м.² ЭПР полуволнового диполя на волне λ = 0,1 м будет равна σ_l = 0,86λ² = 0,86∙10^-2 м.²

.

Следовательно, полуволновый диполь l = 5 см на волне λ =10 см имеет ЭПР σ_l, примерно в 50000 раз большую чем диполь длиной 1 см.

5.2. Динамика образования и статистические характеристики облака отражателей

Пространственно-временные параметры облака отражателей

Чтобы определить информационный ущерб, наносимый пассивными помехами, необходимо знать ЭПР части облака диполей, попадающей в элемент разрешения подавляемой РЛС, в данный момент времени. Последнее требует знания динамики развития облака отражателей после раскрыва пачки, сброшенной постановщиком помех.

Масса диполя и его аэродинамические характеристики обеспечивают ему возможность достаточно свободного перемещения под воздействием воздушных потоков. Практически, большинство действующих диполей пачки совершает случайные блуждания в соответствии с законами турбулентной диффузии атмосферы. Количественные оценки первого приближения, позволяющие ориентировочно оценить параметры облака диполей, могут быть получены на основании рассмотрения простейшей задачи теории одномерных блужданий [65. 66].

В рассматриваемом случае диффундирующую безынерционную частицу представляет диполь, осуществляющий случайные блуждания (флуктуации) под воздействием сил, обусловленных турбулентной диффузией атмосферы. Предполагается, что через интервал времени τ осуществляется дискретное перемещение диполя на расстояние h вправо или влево по оси ОХ. Движение начинается из начала координат (ОХ = 0). Перемещения осуществляются по случайному закону вправо с вероятностью p, влево с вероятностью q.

Параметры τ,h, p и q предполагаются

(5.2.1)

постоянными в течение времени наблюдения.

Определим вероятность того, что через n шагов в момент времени t = nτ диполь удалится от начала координат на расстояние x. Последнее может иметь место, если за время t диполь m раз переместится вправо и (n-m) влево. Соответственно

. (5.2.2)

Искомая вероятность P_n(m) определяется с помощью формулы Бернулли [3, 20]:

, (5.2.3)

где

.

В пределе при τ → 0 и h → 0 от вероятности P_n(m) можно перейти к вероятности P(x,t). Процесс блуждания является Марковским. Опираясь на закономерности Марковских процессов, определим вероятность P(x,t+τ) того, что диполь в момент времени t+τ будет в точке с координатой x. В соответствии с теоремой Маркова, которая в данном случае сводится к формуле полной вероятности, имеем

(5.2.4)

Пользуясь равенством (5.2.1), выражение (5.2.4) можно записать следующим образом:

. (5.2.5)

Для достаточно малых τ и h в (5.2.5) разности вероятностей представляются в виде первых членов соответствующих рядов:

где O(τ) и O(h²) ‑ остатки соответствующих порядков малости. Подставляя полученные выражения для разностей вероятностей в (5.2.4) и опуская достаточно малые величины O(τ) и O(h²), получим:

. (5.2.6)

Переходя к пределу τ → 0 и h → 0, введем ограничения, не допускающие произвольного независимого друг от друга перехода τ и h к пределу. Ограничения предполагают конечность скоростей распространения флуктуаций и их дисперсий. Конкретно это сводится к существованию конечных пределов

(5.2.7)

С учетом сделанных ограничений уравнение (5.2.6) преобразуется к виду

. (5.2.8)

Решение уравнения должно удовлетворять следующему начальному условию:

(5.2.9)

Уравнение (5.2.8) является классическим уравнением диффузии. Оно получено в начале века физиками Фоккером и Планком. В общем виде и достаточно строго оно было выведено А.Н. Колмогоровым. Наиболее широко распространенное его название ‑ уравнение Фоккера-Планка-Колмогорова (ФПК).

Если функция P(x,t) дифференцируема, то уравнение ФПК может быть записано и для плотности вероятности p(x,t):

(5.2.10)

Начальное условие

, (5.2.11)

где δ(x–x₀) ‑ дельта-функция. Когда x₀ = 0 и t₀ = 0, что имеет место в рассматриваемом случае, получим

.

Решение уравнения (5.2.10) может быть получено методом разделения переменных [67]. Если коэффициент сноса A_x и диффузии B_x, постоянны, решение уравнения (5.2.10) при начальных условиях (5.2.11) записывается в следующем виде:

. (5.2.12)

В полученном выражении A_xt равно среднему значению смещения диполя от начала координат (x = 0) за время t,которое в последующем обозначается x₀:

. (5.2.13)

Среднее квадратическое отклонение (СКО) диполя по оси x определяется равенством

. (5.2.14)

Знак осреднения над σ_x, x₀, и другими величинами в данном случае и в последующем опускается.

Характерной особенностью плотности вероятности p(x,t) является ее нестационарность. Параметры σ_x и x₀, зависят от l.

Рис. 5.6

На рис. 5.6 приведена зависимость p(x,t) для двух моментов времени t₁ и t₂ (t₁<t₂), которым соответствуют СКО. и σ_x1 и σ_x2. Предполагается, что A_x = x₀ = 0. Здесь же показана эффективная ширина полосы дипольных отражателей l_Пэ,x(t₂), определяемая СКО σ_x(t₂) и равная

. (5.2.15)

В последующем дисперсию распределения диполей в турбулентной среде обозначаем σ_x²(σ_y²,σ_x²)

. (5.2.16)

Предполагая независимость турбулентной диффузии атмосферы по осям OX, OY и OZ, что в рассматриваемой задаче вполне допустимо, можно записать уравнения ФПК для плотностей вероятностей p(y,t) и p(z,t), с соответствующими начальными условиями, и получить решения, аналогичные (5.2.12). Как известно, процессы турбулентной диффузии атмосферы отличаются от классического случая, описываемого уравнением ФПК с постоянными коэффициентами.

В зависимости от величины дисперсии σ² распределения диполей в турбулентной среде коэффициент турбулентной дисперсии B по разному изменяется во времени, причем

.

Исследования А. А. Загородникова [38, 68] показали, что распределение дипольных отражателей в турбулентной атмосфере при эффективном значении ширины облака l_Пэ ≤ 50 м определяется коэффициентом турбулентной диффузии B, зависящим от времени по квадратичному закону (закону турбулентной диффузии Колмогорова-Обухова). При этом СКО σ_x зависит от времени в степени 3/2

,

где η_x – коэффициент пропорциональности.

Если же 50 м ≤ l_Пэ ≤ 1000 м, то коэффициент турбулентной диффузии изменяется пропорционально времени

.

Соответственно, при больших значениях эффективной ширины облака (l_Пэ ≥ 1000 м) имеет место обычная диффузия B = const, σ = η√t.

На практике наибольший интерес представляет второй случай 25 м ≤ σ ≤ 500 м. Для указанных условий решение уравнения турбулентной диффузии приводит к следующей формуле для трехмерной плотности вероятности p(v,t):

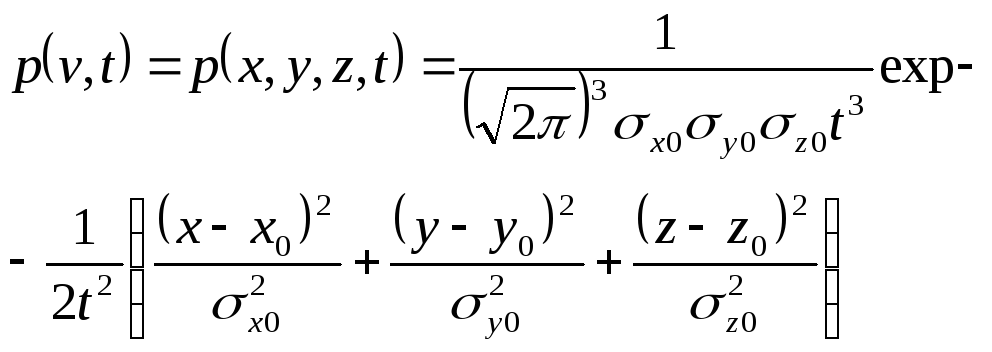(5.2.17)

Здесь:

C_x, C_y, C_z – скорость движения воздуха (скорость течения) соответственно по осям x, y, z.

A_x’, A_y’, A_z’– осредненные скорости ветра по осям x, y, z.