Эффективная площадь рассеяния полуволнового диполя, произвольно ориентированного в пространстве

Согласно определению (4.2.52) ЭПР диполя равна

, (5.1.3)

где 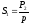– отношение полной переизлучаемой диполем мощности (P₂) к плотности потока мощности (p), падающей на диполь плоской волны;

G₁ ‑ коэффициент направленного действия диполя.

Для диполя, ориентированного под углом Θ к электрическому вектору E падающей волны (рис. 5.1), переизлучаемая мощность P₂ равна

, (5.1.4)

где P₂₀ ‑ мощность, излучаемая диполем в экваториальной плоскости (при Θ = 0).

Рис. 5.1

Как известно [29], значение мощности P₂₀ может быть найдено по формуле

, (5.1.5)

где i ‑ амплитуда тока в пучности;

R_Σ ‑ сопротивление излучения диполя.

Для полуволнового диполя

, (5.1.6)

где E ‑ амплитуда электрического поля принимаемой плоской волны;

R_Σ = 73,3ом - сопротивление излучения полуволнового диполя;

h_д = λ/π – действующая высота полуволнового диполя.

Из вышеприведенных соотношений найдем мощность, переизлучаемую полуволновым диполем

[Вт]. (5.1.7)

Плотность потока мощности падающей волны (абсолютная величина вектора Умова - Пойнтинга) определяется формулой

. (5.1.8)

Таким образом, из (5.1.3), (5.1.7) и (5.1.8) с учетом того, что для полуволнового диполя , окончательно получим

. (5.1.9)

При совпадении поляризаций диполя и падающей волны ЭПР полуволнового диполя будет максимальной

. (5.1.10)

В общем случае Θ представляет собой случайную величину. С достаточной для практики точностью с учетом соображений, высказанных в предыдущем параграфе, можно считать, что случайная величина Θ распределена с равномерной плотностью вероятности в пределах всего телесного угла Ω для всех значений угла φ (рис. 5.1). Это позволяет считать

. (5.1.11)

Для определения среднего значения ЭПР диполя σ_i необходимо найти параметры закона распределения случайной величины Ω.

Предположение о равновероятной ориентации диполей означает, что в пределах любого элементарного телесного угла dΩ, (рис. 5.2) число диполей примерно одинаково. Элементарный телесный угол dΩ, может занимать любое положение с одинаковой вероятностью в пределах всего телесного угла 4π. Поэтому плотность вероятности равна

. (5.1.12)

В дальнейшем будем считать, что ЭПР облака диполей не зависит от соотношения поляризаций приемной и передающей антенн, т.е. иными словами, будем считать, что их поляризации одинаковы. В общем случае следует учитывать различие поляризаций.

Рис. 5.2

Вероятность того, что диполь будет находиться в пределах элементарного телесного угла, dΩ равна

. (5.1.13)

Для того чтобы найти среднее значение ЭПР диполя (математическое ожидание), нужно произвести усреднение величины σ_i определяемой формулой (5.1.9), в пространстве по всему телесному углу Ω = 4π

, (5.1.14)

.

В сферической системе координат элемент поверхности сферы единичного радиуса равен элементу телесного угла

. (5.1.15)

Интегрируя (5.1.14), получим

, (5.1.16)

Отсюда

. (5.1.17)

Таким образом, средняя ЭПР пачки диполей σ_n будет равна:

, (5.1.18)

где N_Пэ = ηN – число эффективно действующих диполей в пачке.

Выше была выведена формула (5.1.9) для определения ЭПР диполя, произвольно ориентированного относительно направления электрического вектора падающей волны. В процессе вывода формулы (5.1.9) считалось, что точки излучения и приема смещены, а угол Θ между электрическим вектором и диполем является случайной величиной.

В ряде случаев важно знать величину ЭПР в направлении, не совпадающем с направлением на источник излучения. Ниже выводится формула для указанного случая.

Пусть направление приема сигнала, отраженного от диполя, составляет угол ψ с направлением на источник облучения (рис. 5.3). Обозначим через Θ угол между диполем и электрическим вектором облучающего поля.

Если σ_Imax = 0,86λ²– ЭПР диполя при ψ = 0 и Θ = 0, то для ψ ≠ 0 и Θ ≠ 0

. (5.1.19)

Интересующее нас значение ЭПР одного диполя определяется как математическое ожидание т.е.

. (5.1.20)

Рис. 5.3

Интегрирование производится в пределах всего телесного угла Ω = 4π.

Заменяя σ(Θ,ψ) и p(Ω) их значениями из (5.1.19) и (5.1.12), а также учитывая известное выражение для дифференциала телесного угла единичного радиуса dΩ = sinΘdΘdφ, получим

(5.1.21)

Второй интеграл выражения (5.1.21) путем преобразования

приводится к сумме табличных интегралов вида:

Таким образом, окончательно получим

, (5.1.22)

или

. (5.1.23)

При ψ = 0 получается общеизвестная формула (5.1.17).

Выражение (5.1.23) позволяет сделать вывод о том, что максимальная мощность рассеяния соответствует углам ψ = 0 и ψ = π, а минимальная – углам ψ = π/2 = 0 и ψ = 3π/2. Величина σ_ψ в направлении минимума (ψ = π/2 = 0 и ψ = 3π/2) соответствует примерно 0,65σ_1max (рис. 5.4).

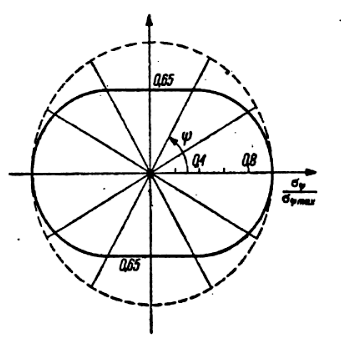
Рис. 5.4

Полученные формулы справедливы для идеально проводящего полуволнового вибратора. Реальные полуволновые диполи вследствие конечной проводимости и толщины обладают большей диапазонностью, чем идеальный полуволновый вибратор. Увеличение длины дипольного отражателя до значений, больших, чем полволны, приводит к уменьшению ЭПР. Однако, при значениях длины диполя, кратных числу полуволн, его ЭПР вновь увеличивается и может быть несколько большей, чем у полуволнового вибратора (рис. 5.5). Последнее не означает, что дипольные отражатели, рассчитанные на подавление более длинноволновых станций, будут эффективны и против РЛС, работающих на более коротких волнах. Дело в том, что число диполей в пачках на более длинных волнах уменьшается, поскольку протяженность пачки фиксирована. Соответственно уменьшается ЭПР пачки на более коротких волнах.

Рис. 5.5

Качественная зависимость ЭПР диполя от его относительной длины приведена на рис. 5.5, где по оси абсцисс отложено отношение длины диполя к половине длины волны.