Статическая балансировка роторов при проектировании
Рис.
11.6
Si,
а далееDi,
тогда для определения величины дисбаланса
корректирующей массы необходимо решить
векторное уравнение (рис.11. 6, б)
рис. 11.6
Технологически балансировку проводят размещением специальных масс привинчиваемых винтами в специальных пазах, высверливанием в «тяжелой» части и т.д. Дисбаланс корректирующей массы определяется по формулеDК = mКrК, где одной из величин задаются (либо « mК», либо «rК»), а вторая рассчитывается. Однако уравновешивание главного вектора сил инерции, т.е. сведения центра масс на ось вращения, недостаточно для полного уравновешивания системы инерционных сил, т.к. в этом случае главная центральная ось инерции тела может пересекать ось вращения ротора в центре масс, но не совпадать с нею.
Динамическая балансировка роторов при проектировании
Динамическое уравновешивание при проектировании проводят с деталями и узлами, в которых массы распределены относительно оси вращения неравномерно, например, детали типа коленчатого вала. Выполняя балансировку можно было бы каждой неуравновешенной массе противопоставлять свою корректирующую массу. Однако такое решение не является целесообразным, так как в системе ротора почти всегда происходит частичное взаимное уравновешивание дисбалансов. Поэтому применяют другой метод.
Рассмотрим ротор, состоящий из деталей 1, 2 и 3. Эти детали делят на несколько дисков и в каждом диске, также как при статическом уравновешивании, определяют величину и направление дисбаланса Di . На детали выбирают две плоскости коррекции (I и II) и каждый вектор дисбаланса раскладывают на две составляющие, расположенные в плоскостях коррекции. Затем составляющие векторы дисбалансов в плоскостях коррекции суммируются и их равнодействующий дисбаланс, уравновешивается соответствующей корректирующей массой mIk . Пример такого уравновешивания изображен на рис. 11.7.
D3 D1 D2 S3 S2 S1 D1II D2II D2I D1I D3I eKII eKI DKII DKI mK2 mK1 m1 m3 l2 l3 L l1 e2 e3 I II D3II m2 Рис. 11.7
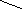
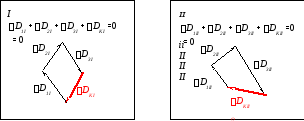
Пространственную систему векторов дисбалансов D1, D2 и D3 заменяем двумя плоскими системами составляющих векторов дисбалансов D1I, D2I, D3I, D1II, D2II, D3II, размещенных в плоскостях коррекции I и II. Условия приведения:
;
;
.
; 
Корректирующие массы mКI и mКII должны быть размещены в плоскостях I и II в местах, определяемых координатами КI, еКI и КII, еКII. Отметим, что вместо корректирующих масс (противовесов) можно применить так называемые «антипротивовесы». Это значит, что на линии действия вектора дисбаланса размещается не корректирующая масса, а диаметрально противоположно ей из ротора удаляется соответствующее количество материала (удаляется, как говорят «тяжелое место ротора»).