Определение ускорений

Для определения ускорений точек В и С записываем уравнения в следующем виде:

Д

Рис. 5.5

алее строим план ускорений (рис. 5.5) в масштабе. Угловое ускорение шатуна (звена 2) определяем по формуле:

.

Экспериментальный метод.

При экспериментальном методе исследования механизмов кинематические характеристики точек и звеньев механизма регистрируются с помощью датчиков. Датчики регистрируют, а потом и преобразуют кинематические параметры в пропорциональные электрические сигналы, которые после усиления регистрируются различными приборами. В последние годы для регистрации и обработки результатов экспериментальных исследований широко используются ПЭВМ. На рис 5.6 показана экспериментальная установка для исследования кинематических характеристик кривошипно-кулисного механизма пресс-автомата.

Рис. 5.6

В этой экспериментальной установке:

• Для измерения перемещения выходного звена используется потенциометрический датчик перемещения, в котором пропорционально положению движка потенциометра изменяется его сопротивление.

• для измерения скорости выходного звена используется идукционный датчик скорости, в котором напряжение на концах катушки движущейся в поле постоянного магнита пропорционально скорости катушки;

• для измерения ускорения выходного звена используется тензометрическиий акселерометр. Он состоит из пластинчатой пружины, один конец которой закреплен на выходном звене механизма, а на втором закреплена масса. На пластину наклеены проволочные тензопреобразователи. При движении выходного звена с ускорением инерционность массы вызывает изгиб пластины, деформацию тензопреобразователей и изменение их сопротивления пропорциональное ускорению выходного звена.

Метод кинематических диаграмм.

Графическое и численное интегрирование.

Этот метод применяется в тех случаях, когда функцию нельзя проинтегрировать в аналитической форме. Численное интегрирование ведётся по квадратурным формулам Ньютона-Котеса, формулам Гаусса.

При заданных значениях функций дляn+1 равноотстоящих значений аргумента квадратурные формулы Ньютона-Котеса имеют вид:

правило трапеций для n шагов

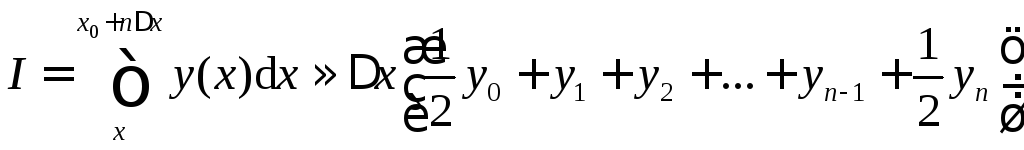
правило трапеций для n=1

правило Симпсона для n=2

правило Уэддля для n=6

При вычислениях на ЭВМ используют программы, имеющиеся в каталоге конкретной машины (например, QTFG или QSF).

При графическом определении интеграла подынтегральная функция задается графиком. Для примера рассмотрим определение угла поворотавыходного звена по заданной кривой, полученной экспериментально.

График угловой скорости изображается в декартовых коор­динатах с учетом числовых значений масштабов: угловой скоростии времени. Промежуток времени отдо, делится на такое количество интервалов, которое позволяет считать, что на каж­дом малом промежутке временидвижение можно принять рав­номерным.

Эти промежутки времени, отмеченные на рис. 5.7 , а точками 0, 1, 2, 3, 4, не обязательно должны быть равными.

В каждом интервале времени, например от доможно при­ближенно считать, что

т. е. можно принять, что площадь криволинейной трапеции равно­велика площади прямоугольника высотой и основанием.

Концы средних ординат для каждого интервала проецируют на ось ординат и соединяют найденные точки 1', 2', 3' , ... ,i' с точкой D, которая ограничивает слева выбранный отрезок интегрирования OD длиной К, мм (рис. 5.7, a).

Лучи D1', D2', D3', ... , проведенные через точку D, образуют углы D1’, с положительным направлением осих, причем .

На искомом графике (рис. 5.7, б) проводят линии 01", 1"2" , 2"3" , ... , параллельные в пределах соответствующих интервалов лучамDl', D2' , D3', ... . Первый отрезок 01" проводят через начало координат 0, следующие отрезки соответственно через точ­ку 1", затем через точку 2" и т. д. Эти линии наклонены относи­тельно положительного направления оси х под углами соответственно, т. е.

Отрезки на графиках связаны с соответствующими физическими параметрами с помощью масштабов соотношениями:

Рис. 5.7

Приравнивая правые части написанных выше соотношений для тангенса углаполучаем:

Откуда масштаб искомого графика:

(5.18)