Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Физика методички по лабам / m36

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

208.41 Кб

Скачать

☆

Московский Государственный Технический университет им. Н. Э. Баумана

А.М.Кириллов, Е.И.Красавина.

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТРЕНИЯ КАЧЕНИЯ МЕТОДОМ НАКЛОННОГО МАЯТНИКА

Методические указания к лабораторной работе М-36 по общему курсу физики. Под редакцией Л.Н. Климова.

Цель работы - экспериментальное изучение основных закономерностей трения качения и измерение коэффициента трения качения для разных материалов.

Теоретическая часть Трение качения возникает при перекатывании цилиндрического юга сфери-

ческого тела по поверхности другого тела. Для примера рассмотрим шар радиу-

сом R. и массой!т, лежащий на горизонтальной поверхности (рис. 1). Приложим к

оси шара силу Q , меньшую, чем максимальная сила трения покоя Fm= N, где -

статический коэффициент трения скольжения, а N - нормальная реакция опоры.

Тогда в точке А возникает сила трения

F , численно равная силе

Q . Если сила

нормальной реакции опоры N приложена в точке А, то она уравновешивает силу

P =

mg , а под действием пары сил

Q и

F будет происходить качение шара.

Рис. 1

Рис. 2

Однако в действительности все происходит несколько иначе. При взаимодействии

шара и плоскости их поверхности деформируются, и касание их происходит

вдоль некоторой области АВ (рис. 2). При действии на шар силы Q равнодейст-

вующая сил реакции опоры имеет точку приложения, смещенную к точке В, т.е. в
!	!

сторону действия силы Q . С увеличением силы Q это смещение растет до неко-

торой величины . В предельном положении на шар будут действовать две пары

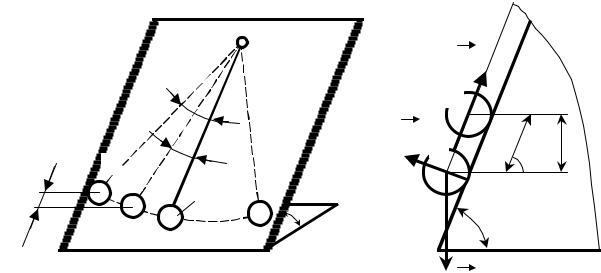
сил с моментами M1=QПРR и М2=µ N, уравновешивающими друг друга. Из равенства моментов M1=М2 находим значение предельной силы

QПР =		N	(1)
	R

Пока Q<QПР, шар покоится. При Q=QПР начинается качение.

Входящая в выражение (1) величина µ носит название коэффициента трения качания.

Коэффициент трения качения µ - это плечо пари сил, создающих момент трения качения, при котором начинается качение без скольжения. Коэффициент µ измеряется в единицах длины. Его значение зависит от материала тела и соприкасающейся с ним поверхности и определяется опытным путем.

Для большинства материалов отношение µ /R значительно меньше, чем статический коэффициент трения скольжения fc.Этим объясняется то, что в технике, когда это возможно, стремятся заменить скольжение качением.

Для исследования трения качения в данной работе использован наклонный маятник (рис. 3).

	2	T
	α 0	T
	α 0
	α n	B
	α n

	N	B′	∆ L	h
	B	B′		h
	B
∆ L	B′			β
	1			β
	1		β
			β
	β

Рис. 3

Шарик 1 массой m подвешен на нити длиной L и давит на наклонную плоскость 2, угол наклона β которой можно изменять.

Если вывести шарик из положения равновесия, он будет катиться по плоскости, и его движение примет характер затухающих колебаний. Коэффициент трения качения с помощью наклонного маятника определяют путем измерения уменьшения амплитуды его колебаний за определенное число периодов.

За n периодов колебания маятника шарик переходит из положения В в по-

ложение В′. При этом маятник теряет энергию ∆	E =mgh, равную работе момента
сил сопротивления при изменении угла отклонения маятника на величину S/R, где
S - длина дуги, которую описывает шарик,	(2)
∆ E=∆ AP + ∆ A1

Здесь ∆ АP - работа момента силы трения качения (∆ АP =MS/R);

∆А1 - работа, затрачиваемая на преодоление сопротивления среда и трения в подвесе маятника;

∆h - изменение положения центра тяжести маятника. Пренебрегая ∆ А1, ввиду ее малости, имеем

mg∆ h=µ NS/R.

Из геометрических соображений (см. рис. 3) найдем Подставив ∆ h и N в выражение (3), получим

mg∆ L sin β = R mg cosβ ,

(3)

∆ h= ∆ Lsinβ и N= mgcosβ .

(4)

где R - радиус шара; ∆ L=L(cosα n - cosα 0) (см. рис. 3), α 0 и α n - амплитудные значения угла отклонения маятника от положения равновесия в начальный момент и через n полных колебаний соответственно.

Из выражения (4) определяем коэффициент трения качения
µ =	R	tgβ	L(cosα		n−	cosα	0 )	(5)

	S
Путь, который проходит центр тяжести маятника за n колебаний,								(6)
			S=4nLα		СР		2
При малых углах α 0 и α n, учитывая, что				cosα		1− α
				α	0 −α		2 , получим
µ =			Rtgβ			n		(7)
					4n

где α 0 и α n - выраженные в радианах углы отклонения маятника в начальный и конечный моменты наблюдения.

Экспериментальная часть Описание установки

Установка для определения коэффициента трения качения представлена на рис. 4.

На вертикальной стойке 2 основания 1 размещен червячный редуктор, который осуществляет поворот и фиксацию нижнего кронштейна 3. Червячный редуктор приводится во вращение маховичком, причем угол наклона образца отсчитывается по шкале 4. Нижний кронштейн 3 представляет собой литую деталь сложной конфигурации, на которой крепятся: шкала отсчета амплитуда колебаний маятника 5; вертикальный стержень 6, предназначенный для крепления верхнего кронштейна 7; фотоэлектрический датчик 9.

Шкала 5 представляет собой пластинку, в которой выфрезеровано гнездо, предназначенное для установки сменных образцов. По шкале определяется угол отклонения маятника, от положения равновесия до 11°. Шкала 5 снабжена зеркальным отражателем, который служит для уменьшения параллакса при отсчете угла отклонения маятника.

Образец представляет собой прямоугольную пластину, имеющую две рабочих поверхности с разной шероховатостью. В верхнем кронштейне 7 размещается механизм подвеса маятника, который позволяет регулировать его длину. Маятник

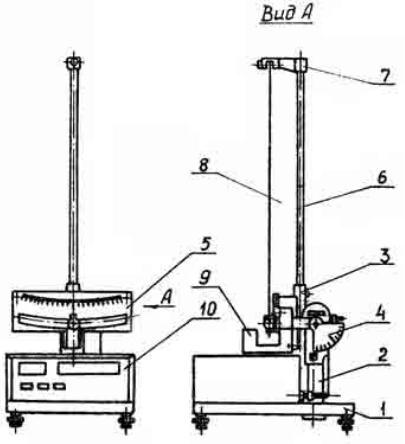
3 - тонкая эластичная нить с подвешенным на ней шаром, который в свою очередь имеет конус, предназначенный для пересечения оптической оси фотоэлектрического датчика 9. Фотоэлектрический датчик 9 расположен на нижнем кронштейне и служит для выдачи электрического сигнала на физический миллисекундомер 10, выполненный как самостоятельный прибор с цифровой индикацией времени и количества полных периодов колебаний маятника.

Рис. 4

Подготовка установки к работе.

1.Установить в гнездо шкалы исследуемый образец.

2.Произвести регулировку положения основания при помощи регулировочных опор таким образом, чтобы нить подвеса маятника совпала с нулевым делением шкалы.

3.Установить с помощью маховичка угол наклона образца, равный 90°; при этом шарик должен касаться исследуемой поверхности образца при отсутствии силы нормального давления, что достигается с помощью регулировочных опор.

4.Установить угол наклона образца 60°.

5.Отрегулировать длину маятника с помощью устройства на верхнем кронштейне таким образом, чтобы, при колебаниях маятника шарик перемещался по рабочей поверхности образка, не касаясь шкалы.

6.Подключить к разъему "Вход" на миллисекундомере фотоэлектрический датчик.

7.Включить в сеть шнур питания миллисекундомера.

6. Нажать кнопку "Сеть", расположенную на лицевой панели миллисекундомера; при этом должны загореться цифровые индикаторы. 9. Отклонить маятник на угол 5-6°, нажать кнопку "Сброс" на лицевой панели миллисекундомера и плавно отпустить маятник. Убедиться, что маятник совершает колебательные движения, а миллисекундомер производит отсчет времени и количества полных периодов колебаний маятника.

10. После совершения маятником 15-20 колебаний нажать на кнопку "Стоп" миллисекундомера, при этом убедиться, что счет времени и количества полных периодов колебаний прекращается в момент окончания очередного периода колебаний маятника,

Выполнение эксперимента.

1.Протереть рабочие поверхности исследуемого образца неворсистой тканью, смоченной в спирте,

2.Установить угол наклона образца 45°,

3.Отклонить маятник от положения равновесия на угол α 0=6°. Нажать на кнопку "Стоп" миллисекундомера при достижении амплитуды колебаний маятника

α n=2°. Снять показания миллисекундомера о количестве полных периодов колебаний маятника.

4. Результаты эксперимента занести в соответствующие графы таблицы.

№ образца	β	α	α	n	µ		∆µ	ε

5.Аналогичные измерения произвести для углов наклона образца 30о и 60о.

6.Заменить исследуемый образец и провести для него эксперимент по пунктам 1-

Окончательный результат эксперимента для каждого образца представить в виде

= ± ∆ .

Чтобы рассчитать ∆µ , воспользуемся выражением для полуширины доверительного интервала, результата косвенных измерений:

∂ µ 2

∂ µ

∂µ

(8)

∆ µ =

∆

R +

∂

∆α

∆

∂ R

∂

Подставляя значение , определенное по формуле (7), получим

= (α

tgβ )

( R tgβ )

(9)

∆ µ

∆

R +

∆α

∆ β

cos

где ∆ R, ∆α

и ∆β - абсолютные погрешности прямых измерений R, α

и β ,

0 −α

α =

, а

∆α

0 )

∆α+

(

n ) .

(

Преобразуем выражение (9) к виду, удобному для вычислений:

∆µ

∆

∆α

∆β

∆

(

∆α

0 )

2 + ∆α

(

n ) ∆β

(α 0 −α

n )

2 +

sin 2

sin 2β

Абсолютные погрешности ∆

R, ∆α

0, ∆α

n и ∆β

принять равными цене деления соот-

ветствующих шкал.

Контрольные вопросы

1.Что является причиной трения между телами?

2.Что понимают под коэффициентом трения качения?

3.Зависит ли величина коэффициента трения от силы давления тела на поверхность соприкосновения?

4.Зависит ли величина силы трения от площади соприкасающихся поверхностей?

5.Показать графически зависимость силы трения от силы давления при постоянном коэффициенте трения.

Литература

1.Савельев И.В. Курс общей физики, т. 1. - М.: 1982. - 432 с.

2.Лабораторный практикум по физике /Под ред. А.С.Ахматова. - М.: 1980. - 360 с.

Соседние файлы в папке Физика методички по лабам

#
10.02.2015248.05 Кб24m13.pdf
#
10.02.2015177.28 Кб17m16.pdf
#
10.02.2015175.38 Кб37m20_m21.pdf
#
10.02.2015154.86 Кб27m23.pdf
#
10.02.2015170.34 Кб22m30.pdf
#
10.02.2015208.41 Кб19m36.pdf
#
10.02.2015203.86 Кб16m4.pdf
#
10.02.20152.45 Mб17m40.pdf
#
10.02.2015350.85 Кб16m6.pdf
#
10.02.2015203.27 Кб30m7ab.pdf
#
10.02.2015206.1 Кб43m8.pdf