Учебная литература / Геометрические и кинематические характеристики механизмов
.pdf
Таким образом, маховик является аккумулятором энергии, получаемой от механизма, когда положение звеньев
представляет наилучшее для работы состояние. Поскольку масса маховика значительна, то при прохождении мёртвого положения кинетическая энергия маховика проворачивает кривошип.Дальше действует сила ползуна.
Кинематический способ используется в тех случаях, когда большие массы маховиков недопустимы. Этот способ заключается в том, что кривошипы нескольких одинаковых механизмов жёстко связаны между собой образуя коленчатый вал. У этих кривошипов общая ось вращения, но расположены они под углом друг к другу, чтобы при мёртвом положении одного механизма, другой имел более благоприятное положение, и проворачивал коленчатый вал остальных механизмов. В этом случае также могут быть использованы маховики, но они будут иметь очень незначительную массу.
На рис.3.19 первый и третий механизмы находятся в мёртвых положениях, а второй и четвёртый механизмы находятся внаилучших положениях.
Рис.3.19
Пример 5.
Используемметод замкнутых векторных контуров(рис.3.7).
Рис.3.20.Замкнутый векторный контур кривошипноползунного механизма
Решение:
Рассмотрим замкнутый векторный контур OABCO. Соблюдая единообразие отсчёта углов, определяющих положение звеньев,составимвекторное уравнение
. |
(4) |
Спроектируем(4) |
на координатные оси Х и Y: |
(5)– (6)
|
Решение задачи о положениях |
|
|
|
|
|
Определим функции положения ползуна |
|
и шатуна |
. Из (6) получаем |
, |
откуда |
,из(5)получаем |
|
|
. |
|
|
Решение задачи о скоростях |
|
|
|
|
|
Определиманалогскорости ползуна |
и шатуна |
,для чего продифференцируемуравнение (5)и (6): |
|
|
Из(8)получаеманалогскорости шатуна |
|
(7)(8) |
|
|
|
, |
|
|
тогда угловая скорость шатуна |
. |
|
Из(7)получаеманалогскорости ползуна |
|
|
|
|
, |
тогда скорость ползуна вычисляется по формуле |
. |
|
Решение задачи об ускорениях |
|
|
Определим аналоги ускорений шатуна |
и ползуна |
, для чего продифференцируем уравнения по |
(7)и (8):
(9)(10)
Из (10) получим аналог ускорения шатуна , тогда угловое ускорение шатуна можно вычислить по формуле
.
Из(9)получиманалогускорения ползуна |
,тогда ускорение ползуна можно вычислить по формуле |
.
Аналитическое исследование шарнирного четырёхзвенного механизма
Рис.3.21
При ведущем кривошипе рабочим ведомым звеном является чаще всего коромысло 
(рис.3.21). Чтобы найти зависимость угла поворота ведомого звена от ведущего аналитическим способом пользуются следующей формулой (рис.3.22):
.
Рис.3.22
Аналитическое исследование кривошипнокулисного механизма
Основнымэлементомкривошипнокулисных механизмовявляется кулиса. Кулиса – подвижная направляющая ползуна.
Кулисы бывают прямолинейные и изогнутые (рис.3.23). Конструктивно они бывают выполнены в виде стержней или рамных направляющих.
Рис.3.23
По принципу действия кривошипнокулисные механизмы бывают следующих видов: механизмы с возвратно поступательнымвращениемкулисы,механизмы с вращательнымдвижениемкулисы.
Рассмотриммеханизмс поступательнымвращениемкулисы (рис.3.24). 1 – кривошип.
2 – ползун (камень).
3 – кулиса.
; 
; 
.
Рис.3.24
Назначением таково механизма является преобразование вращательного движения кривошипа в возвратно поступательное движение кулисы.
Кулисный механизмс вращающейся головкой (рис.3.25).
Рис.3.25
1 – кривошип.
2 – ползун.
3 – качающаяся кулиса.
Этот механизм предназначен для преобразования вращающегося движения кривошипа в колебательное или вращательное движение кулисы (рис.3.26).
Рис.3.26
Зададим
.
угол поворота кривошипа при переходе кулисы изкрайнего правого вкрайнее левое положение. 
угол поворота кривошипа при переходе кулисы изкрайнего левого вкрайнее правое положение.
Очевидно,что угол |
больше угла |
.Таккак |
|
,то |
,а |
; |
или |
. Так как |
|
, то |
. Это означает, что прохождения кулисы влево и |
||
вправо различны,то есть влево кулиса двигается медленнее,чемвправо.
Средняя скорость точки 
: 
; 
.
Путь .
;.
Найдёмзависимость угла поворота кулисы от угла поворота кривошипа:
; |
. |
;
;
; |
; |
; |
. |
Выше были рассмотрены механизмы, у |
которых |
радиус кривошипа |
был меньше чем межцентровое |
расстояние 
.В этих механизмах кулиса совершала колебательные движения.
Рассмотрим вариант, когда радиус кривошипа будет больше межцентрового расстояния 
(рис.3.27). В этом случае центр вращения кулисы – точка 
будет находиться внутри кривошипной окружности, очерчиваемой шарниром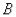
кривошипа.Такие механизмы имеют вращающуюся кулису.
Таккакрадиус величина переменная, то угловая скорость кулисы тоже будет величиной переменной. Верхнюю часть окружности кулиса проходит медленнее,чемнижнюю
Рис.3.27
Вопросы для самопроверки
Что называется "функцией положения"для звена или точки механизма?
В чемразличие между кинематическими и геометрическими характеристиками механизма?
Какие функции называются кинематическими передаточными функциями механизма?
Какие передаточные функции механизма называются главными,а какие вспомогательными?
Перечислите методы геометрокинематического исследования механизмов?
Напишите формулы,устанавливающие связь между геометрическими и кинематическими характеристиками механизма?
Изложите суть метода "проекций векторного контура"?
Что называется циклом?
Что называется "центроидой",какцентроиды используются при кинематическомисследовании механизма?
Какметод кинематических диаграммприменяется при кинематическомисследовании механизмов?
Какприменяется метод преобразования координат при решении прямой задачи о положении точки выходного
звена?
Каккинематические характеристики определяются экспериментально?
Опишите последовательность кинематического анализа плоского механизма.
Запишите уравнения плановскоростей и ускорений для любой структурной группы IIкласса,содержащей внутреннюю поступательную пару.
Запишите уравнения плановскоростей и ускорений для любой структурной группы IIкласса,содержащей хотя бы одну внешнюю поступательную пару.
Какопределяют величину и направление ускорения Кориолиса?
В каких случаях при построении плановскоростей и ускорений применяют метод подобия?
По какому признаку можно установить,является ли равномерным(или неравномерным)относительное движение звеньев,образующих поступательную пару?
Цель кинематического анализа механизмов.
Ответ: изучить движение звеньевмеханизма безучета сил,вызывающих это движение.
Какназываются графики,построенные по полученнымзначениямкинематических величин? Ответ: кинематические диаграммы.
Назовите численные значения масштаба.
Ответ: 1,2,2.5,4,5.
Какназывается чертеж,на которомизображены ввиде отрезковвекторы,равные по модулю и по направлению ускорениямразличных точекзвеньевмеханизма вданный момент?
Ответ: план ускорений.
Единица измерения масштаба скорости.
Ответ: мсек1/мм.
Напишите формулу для определения численного значения нормальной составляющей ускорения любой точки кривошипа.
Ответ: 
.
Какопределить направления угловой скорости звена?
Ответ: угловая скорость и вектор относительной скорости направлены водну сторону.
Скорость самолета 2500 км/час.Сколько метровсамолет пролетает за одну секунду? Ответ: 694,4 м/сек.
Скорость автомобиля 80 км/час.Какой путь автомобиль пройдет за одну секунду? Ответ: 22 м.
Задачи кинематического анализа механизмов.
Ответ: определение перемещений звеньеви траекторий,описываемых точками звеньев; определение скоростей отдельных точекзвеньеви угловых скоростей звеньев; определение ускорений отдельных точекзвеньеви угловых ускорений звеньев.
Понятие масштаба вТММ.
Ответ: Масштаб это отношение действительной величины котрезку вмм,который изображает эту величину на чертеже.
Напишите формулу для определения численного значения скорости любой точки кривошипа. Ответ: .
Чемзадается положение ведущего звена,если оно входит впоступательную пару? Ответ: функцией перемещения s=s(t).
Какопределить направление углового ускорения звена?
Ответ: угловое ускорение направлено всторону тангенциальной составляющей относительного ускорения.
С какой целью определяют ускорения точекзвеньевмеханизма? Ответ: например,для определения силы инерции.
Для каких целей строят кинематические диаграммы?
Ответ: для кинематического исследования механизма.
Единица измерения масштаба времени. Ответ: сек/мм.
Чемопределяется положение ведущего звена,если оно входит во вращательную пару со стойкой?
Ответ: функцией угла поворота 
.
С какой целью определяют перемещения (траектории)точекзвеньевмеханизма?
Ответ: для построения кинематических диаграмм,а также для выбора размеровкорпусных деталей при проектировании механизма.
Напишите формулу для определения угловой скорости 
(рад/сек),если известна частота вращения 
(об/
мин).
Ответ: 
.
Единица измерения масштаба длины. Ответ: м/мм.
Напишите формулу для определения численного значения тангенциальной составляющей ускорения любой точки кривошипа.
Ответ: .
С какой целью определяют скорости точекзвеньевмеханизма? Ответ: например,для выбора типа смазки.
Единица измерения масштаба угла поворота.
Ответ: град/ммили рад/мм.
Что такое кинематические диаграммы?
Ответ: графики,построенные по полученнымзначениямкинематических величин. Что такое план скоростей?
Ответ: чертеж,на которомизображены ввиде отрезковвекторы,равные по модулю и по направлению скоростямразличных точекзвеньевмеханизма вданный момент.
Что такое план ускорений?
Ответ: чертеж,на которомизображены ввиде отрезковвекторы,равные по модулю и по направлению ускорениямразличных точекзвеньевмеханизма вданный момент.
Задачи для самостоятельного решения
Задача 1
Для некоторой структурной группы имеется уравнение плана скоростей
.
Написать для этой группы:
1)уравнение плана ускорений;
2)формулы для вычисления угловой скорости и углового ускорения звена 3.
Задача 2
Кривошип OA механизма вращается равномерно; обозначить полюс и все векторы плана ускорений. Считая все
постоянные размеры звеньевзаданными,нанести на этот план вектор 
ускорения точки C.
Задача 3
Кривошип OA механизма вращается равномерно; обозначить полюс и все векторы плана ускорений.Считая все
постоянные размеры звеньевзаданными,указать на прямой AB звена 2 такую точку C,ускорение которой направлено,какпоказано на рисунке (написать формулу,по которой вычисляется положение этой точки на звене). Нанести соответствующую точку на план ускорений.
Задача 4
На плане скоростей кривошипнокулисного механизма отметить полюс и векторы скоростей всех
обозначенных на схеме точек.Найти для изображенного положения механизма точную величину отношения ( |
), |
если OA = OB. |
|
Задача 5
Для структурной группы имеется уравнение плана ускорений
.
Написать для этой группы: |
|
|
|
1) |
уравнение плана скоростей; формулы для расчета угловой скорости |
и углового ускорения |
; |
2) |
формулы для расчета нормального и кориолисова ускорений. |
|
|
Задача 6
В рассматриваемомположении механизма звенья 1 и 3 вертикальны,звено 2 горизонтально.Звено 1 вращается
равномерно с угловой скоростью =10 рад / с.Длины звеньев: AB = BC = 2OA.Найти величину и направление углового ускорения звена 2.
Задача 7
В рассматриваемомположении механизма звенья 1 и 3 вертикальны,звено 2 горизонтально.Звено 1 вращается
равномерно с угловой скоростью =10 рад/с.Длины звеньев: AB = BC = 2OA.Найти величину и направление углового ускорения звена 2.
Задача 8
Определить скорость и ускорение точки B звена 2; указать направления обоих векторовдля заданного положения механизма.
Исходные данные: OA=0,20 м; AB=0,10 м; 
=5 рад/с; кривошип OA втекущемположении вертикален.
Задача 9
Для механизма крестовокулисной муфты определить скорость и ускорение точки B звена 3; указать направления обоих векторов.В текущемположении механизма звено 1 вертикально и вращается равномерно с угловой
скоростью 
= 10 рад/с,звено 3 отклонено от вертикали на угол 
=300.Размер АВ = 0,3 м.
Задача 10 |
|
|
В текущемположении механизма угол |
ползун 1 движется равномерно.Размеры звеньев: длина |
|
кривошипа |
,длина шатуна |
.Определить точное соотношение угловых ускорений звеньев |
вуказанномположении.
Задача 11 (см.рисуноккзадаче 10)
Установить величину отношения угловых ускорений звеньев2 и 3 
при равномерномдвижении
ползуна 1 визображенномположении кривошипноползунного механизма (т.е.при угле |
).Соотношение длин |
|
звеньев: |
. |
|
Задача 12 (см.рисуноккзадаче 10)
Доказать, что при равномерном движении ползуна 1 в изображенном положении механизма (т.е. при угле
)угловые ускорения звеньев2 и 3 одинаковы по величине и направлению.
Задача 13
Кривошип 1 вращается с угловымускорением 
=1 рад/с2; при какомзначении его угловой скорости 
ползун 3 врассматриваемомположении механизма (т.е.при угле |
)будет двигаться равномерно? |
|
Соотношение длин звеньев: |
. |
|
Задача 14
Для кинематической цепи известны: размеры звеньевBC и h; положение,скорость 
и ускорение 
точки
A; положение (угол ),угловая скорость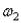
и угловое ускорение
звена 2; положение,скорость
и ускорение
точки B.Описать порядокпостроения положения точки С; написать уравнения плановскоростей и ускорений,в результате решения которых будут найдены скорость и ускорение точки С,а также угловая скорость и угловое ускорение звеньев3 и 4.