
- •Введение
- •1 Основные понятия и определения. Классификация механизмов
- •1.1 Основные понятия и определения
- •1.2 Кинематические пары и их классификация
- •1.3 Кинематические цепи и их классификация
- •1.4 Структурные, кинематические и конструктивные схемы механизмов
- •1.5 Общая классификация механизмов
- •1.5.1 Механизмы, преобразующие вид движения
- •1.5.2 Механизмы, преобразующие параметры движения
- •2 Анализ рычажных механизмов
- •2.1 Структурный анализ
- •2.2 Кинематический анализ
- •2.2.1 Основные кинематические характеристики механизмов
- •2.2.2 Цели, задачи и методы кинематического анализа
- •2.2.3 Графический метод дифференцирования (метод кинематических графиков)
- •2.2.4 Метод планов скоростей и ускорений
- •2.2.5 Понятия об аналитических методах
- •2.3 Силовой анализ
- •2.3.1 Задачи и методы силового анализа
- •2.3.2 Определение внешних сил
- •2.3.3 Трение в кинематических парах
- •2.3.4 Механический КПД машины
- •2.3.5 Определение сил реакций в кинематических парах
- •2.3.6 Кинетостатика ведущего звена (рисунок 2.54)
- •2.3.7 Определение уравновешивающей силы методом Жуковского
- •3 Анализ зубчатых механизмов
- •3.1 Основной закон зацепления (теорема Виллиса)
- •3.2 Теория эвольвенты
- •3.4 Основные параметры эвольвентных зубчатых колес
- •3.5 Способы изготовления зубчатых колес
- •3.6 Основные параметры зубчатой пары
- •3.7 Построение картины внешнего эвольвентного зацепления
- •3.8 Качественные показатели зацепления
- •3.9 Блокирующий контур
- •3.10 Кинематический анализ механизмов передач
- •3.10.1 Аналитический метод
- •3.10.2 Графоаналитический метод
- •3.11 Силовой анализ передач
- •4 Анализ кулачковых механизмов
- •4.1 Общие сведения
- •4.2 Силовой анализ
- •5 Синтез рычажных механизмов
- •5.1 Структурный синтез
- •6 Синтез планетарных механизмов
- •7 Синтез кулачковых механизмов
- •7.1 Графический метод
- •7.1.1 Законы движения ведомого звена
- •7.1.3 Определение основных размеров кулачкового механизма
- •7.1.4 Построение профиля кулачка
- •7.2 Аналитический метод
- •7.2.1 Аналитическое описание закона движения толкателя
- •7.2.2 Определение основных размеров кулачка
- •7.2.3 Построение центрового профиля кулачка
- •7.2.4 Определение радиуса ролика
- •7.2.5 Построение конструктивного профиля кулачка
- •8. Динамика машин с жесткими звеньями
- •8.1 Определение масс и моментов инерции звеньев
- •8.2 Приведение масс
- •8.3 Приведение сил
- •8.4 Режим работы машины
- •8.5 Уравнение движения
- •8.6 Неравномерность хода машинного агрегата
- •8.7 Расчет маховика без учета характеристик приводного электродвигателя
- •8.8 Динамика машин с учетом характеристик приводного электродвигателя
- •9 Динамика машин с учетом упругости звеньев
- •9.1 Структура динамического расчета
- •9.2 Динамические модели
- •9.3 Математические модели
- •9.4 Решение уравнений движения
- •9.5 Оптимизация колебательного процесса
- •10 Уравновешивание и виброзащита машин
- •10.1 Уравновешивание машин
- •10.1.1 Уравновешивание вращающихся звеньев
- •10.1.2 Уравновешивание плоских рычажных механизмов (циклических механизмов)
- •10.2 Виброзащита машин
- •10.2.1 Виброгашение
- •10.2.2 Виброизоляция
- •11 Манипуляторы и промышленные роботы
- •11.1 Виды манипуляторов и промышленных роботов
- •11.2 Структура и геометрия манипуляторов
- •11.3 Кинематика манипуляторов
- •12 Синтез системы управления механизмами машины-автомата
- •12.1 Тактограмма движения
- •12.2 Таблица включений (таблица 12.2)
- •12.3 Составление формул включения и их упрощение
- •12.4 Построение системы управления на пневматических элементах
- •12.5 Построение системы управления на электрических элементах
- •Список использованных источников
Векторное уравнение без ω 2
m1r1l1 + m2r2 l2 + m3r3l3 + mур/ rур/ lур/ = 0.
Строим многоугольник моментов в mrlμ кгм2/мм. Из плана моментов находим величину и направление динамического дисбаланса (рисунок 10.5)
mур/ rур/ lур/ = mур/ rур/ lур/ × mrlμ .
Уравновешивающие массы m'ур устанавливаются одна в плоскости коррекции, другая масса m'ур в любой точке вала.
Противовесы массой mур и m'ур , установленные в одной плоскости
коррекции, можно заменить одной массой, следовательно, полное уравновешивание масс, закрепленных на валу, может быть достигнуто установкой двух противовесов, центры масс которых будут лежать в двух произвольно выбранных плоскостях.
10.1.2 Уравновешивание плоских рычажных механизмов (циклических механизмов)
Для обеспечения приближенного постоянства сил и моментов (рисунок 10.6), действующих на фундамент принимают условия
1) |
|
ин = 0 , |
2) |
|
ин = 0 , |
F |
М |
которым можно удовлетворить подбором масс звеньев и установкой противовесов, т.е. уравновешиванием масс механизма.
Рисунок 10.6 |
Рисунок 10.7 |
При уравновешивании масс плоских механизмов часто ограничиваются выполнением условия (1), что равносильно постоянству положения общего центра масс механизма относительно стойки, т.е. статическое уравновешивание масс механизма.

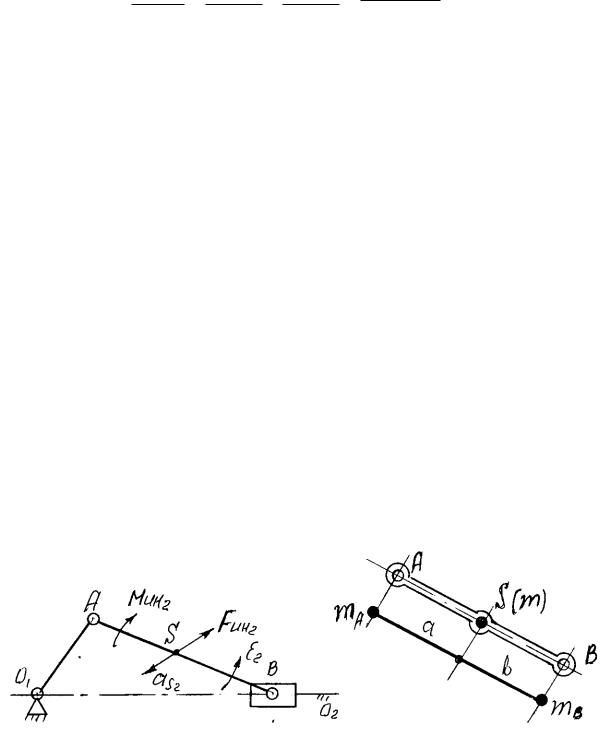
Для нахождения общего центра тяжести механизма применяется метод замещающих точек. Возьмем реальное звено массой m сосредоточенной в центре масс S (рисунок 10.7). Разнесем массу по двум точкам А и В, лежащим на одной прямой с центром тяжести S.
4 Полная масса звена должна не изменяться
m = mA + mB . |
(10.1) |
5Центр тяжести фиктивного звена должен совпадать с реальным звеном
|
|
|
mAa = mBв. |
|
(10.2) |
|
Отсюда mA = mB |
в |
, подставляем в (10.1) |
|
|||
|
а |
|
|
|
|
|
m = mB |
в |
+ mB ,m = mB |
в + а |
,mB = m a |
||
|
|
а |
|
а |
|
l |
|
|
mB = m a ,mA |
= m |
в |
(10.3) |
|
|
|
|
l |
|
l |
|
Определим центр масс для шарнирного четырехзвенника (рисунок
10.8).
Дано: m1, m2, m3, сосредоточенных в центрах тяжести S1, S2, S3, кг; a1, в1, a2, в2, a3, в3 , положение центров тяжести;
m = m1+m2+m3, общая масса мехинизма, кг.
Рисунок 10.8

Распределим массы по шарнирным точкам по формулам (10.3), кг
|
|
m |
O1 |
= m |
1 |
в1 |
,m |
A |
|
= m |
A1 |
+ m |
A2 |
|
|
= m |
1 |
a1 |
|
|
+ m |
2 |
|
в2 |
, |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
l1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 |
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
m |
B |
= m |
B2 |
+ m |
B3 |
= m |
2 |
|
a2 |
|
|
+ m |
3 |
|
|
в3 |
|
,m |
O2 |
|
|
= m |
3 |
|
a3 |
. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Из О1 проводим вектора r1 = |
O1A |
|
, r2 = |
|
|
|
O1B |
|
, r3 = |
O1O2 |
|
, тогда |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
mAr1 |
+ |
|
mBr2 |
+ |
|
|
mO2 r3 |
= |
|
|
|
mrs |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(10.4) |
|||||||||||||||||||||||||||||||||||||||||||||
где |
m = m1 + m2 + |
m3 = mO1 |
|
+ mA + mB + |
|
|
mO2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
rs - радиус-вектор до центра тяжести. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
Введем новую систему векторов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 ,r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
r1 = l |
|
= l |
1 + l2 ,r3 |
|
= |
|
l1 + l2 + |
l3 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(10.5) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и подставим в уравнение (10.4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
mA l1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
+ mB (l |
1 + l2 ) + mO2 (l1 + l2 + l3 ) = mrs , |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
или |
|
(mA + |
mB + |
|
|
|
|
|
|
|
(mB + |
|
|
|
|
|
2 + |
|
|
|
|
|
3 = |
|
|
. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mrs |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
mO2 )l1 + |
|
|
|
mO2 )l |
mO2 l |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Откуда |
mA + mB |
+ mO |
|
|
|
|
|
|
|
|
|
|
|
|
|
mB |
+ mO |
|
|
|
|
|
|
|
|
|
|
|
|
|
mO |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, (10.6) |
|||||||||||||||||||||||||||||||||
|
r = |
2 |
|
|
l |
1 |
+ |
|
|
2 |
|
l |
2 |
+ |
2 |
l |
3 |
= h |
1 |
+ |
h |
2 |
+ h |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
s |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
причем
h1 < l1 и h1 l1 , h2 < < l2 и h2 l2 ,
h3 < < < l3 и h3 l3 .
Таким образом вектор общего центра масс может быть определен как геометрическая сумма векторов h1 , h2 , h3 .
Строя механизм в нескольких положениях, можно получить траекторию центра тяжести.
Для уравновешивания механизма необходимо добиться, чтобы центр тяжести его был в одном и том же месте. Для этого необходимо добиться условия
|
|
|
|
|
|
|
|
3 |
≈ (0,7) , |
|
h |
1 = |
h |
2 = |
h |
(10.7) |
|||||
|
|
|
|
|
|
|
||||
|
|
l2 |
|
|||||||
l1 |
l3 |
|
||||||||
т.е. нужно выровнять коэффициенты с массами в уравнении (10.6). Практически устанавливают противовесы для масс mA и mB (массы mO1 и
mO2 неподвижны) (рисунок 10.9).
|
|
|
1/ |
|
|
|
1 , примем − (mAур |
|
|
|
|
mAур l |
= mA l |
= mA , l1/ |
= |
l1 ) , |
|||||||
|
|
3/ |
|
|
3 , примем − (mBур |
= mB , l3/ |
|
l3 ). |
|||
mBур l |
= mB l |
= |
|||||||||
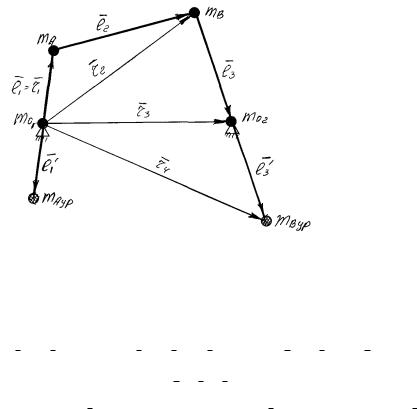
Рисунок 10.9
|
|
|
|
|
|
mrs = − mAур l |
1 + mA l1 + mB r2 + mO2 r3 + mBур r4 . |
(10.8) |
|||
Подставим (10.5) в (10.8)
mrs = mB (l1 + l2 ) + mO2 (l1 + l2 + l3 ) + mB (l1 + l2 + 2l3 ). Сгруппируем массы при векторах l1 , l2 , l3 .
mrs = (mB + mO2 + mB )l1 + (mB + mO2 + mB )l2 + (mO2 + 2mB )l3 . Радиус вектора по центру масс всего механизма
|
|
2mB + mO |
|
|
|
|
|
|
2mB + mO |
|
|
|
|
|
2mB + mO |
|
|
|
|
|
(10.9) |
|
r |
= |
2 |
l |
1 |
+ |
2 |
l |
2 |
+ |
2 |
l |
3 |
= const |
|||||||||
|
|
|
|
|
|
|
||||||||||||||||
s |
|
m |
|
|
|
|
m |
|
|
|
|
|
m |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Массу каждого противовеса mAур |
и mBур |
и расстояния до центров О1 |
||||||||||||||||||||
и О2 можно в некоторых пределах варьировать, но так, чтобы были выполнены условия
mA l1 = mAур l1/ и mB l3 = mBур lB/ .
Аналогично могут быть решены задачи статического уравновешивания других плоских механизмов.
В некоторых случаях уравновешивание масс механизма приводит к неконструктивному расположению противовесов. Например, для статического уравновешивания кривошипно-ползунного механизма (рисунок 10.10) необходимо поставить противовесы не только на кривошип, но и на шатун. Если ограничиться одним противовесом на кривошипе, то это будет задача о приближенном статическом уравновешивании масс механизма, которую можно решить путем статического размещения масс звеньев по точкам О, А, В.
Дано: m1, m2, m3, l1, l2, а1, в1, а2, в2.
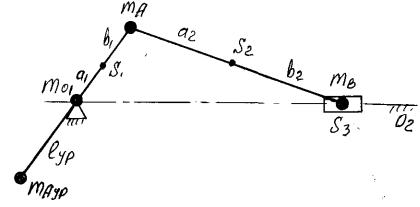
Рисунок 10.10
Разнесенные массы
mO1 |
= m1 |
в1 |
, mA = m1 |
a1 |
+ m |
в2 |
, mB = m3 |
+ m2 |
a2 |
. |
|
|
|
|
|||||||
|
|
l1 |
l1 |
l2 |
|
l2 |
||||
Массу в точке О1, как неподвижную не учитываем.
Сила инерции массы mА полностью уравновешивается противовесом mAур при выполнении условия
mAур lур = mA l1 .
Остается неуравновешенной только сила инерции от массы, которая направлена вдоль движения ползуна. В некоторых случаях эта сила не оказывает вредных влияний на фундамент и тогда такие частичные уравновешивания допустимы.
Уравновесим горизонтальную силу инерции массы mВ Fин = mB l1ω 12 cos ϕ 1 (сила инерции 1 порядка).
Если на дисках 1 и 2 (рисунок 10.11) вращающихся в противоположных направлениях с одинаковыми угловыми скоростями, укрепить массы с равными статическими моментами относительно осей вращения, то для любого положения дисков, проекции этих сил инерции на вертикальную ось уравновешиваются, а на горизонтальную – складываются. Тогда равнодействующая силы инерции представляет собой простую гармоническую функцию
2Fг |
= 2ω 2 |
m |
r сosϕ |
y |
. |
(10.10) |
ур |
ур |
|
ур ур |
|
|
