
Учебная литература / ulstu2012-116
.pdf
2.6.2 Подбор момента инерции Jм маховика по заданному коэффициенту неравномерности δ
Обычно требуется определить параметры маховика при заданных
значениях ωср |
и δ. |
Существуют два |
наиболее распространенных |
|
метода определения Jм – Н. И. Мерцалова |
и метод Ф. Виттенбауэра. |
|||
Рассмотрим |
более |
точный метод |
Ф. |
Виттенбауэра, при котором |
предварительно строится диаграмма энергомасс ∆Тпр(Jпр). Согласно этой диаграмме
(рис.2.38): ω2max,min=2·μТ/μJ·tgΨmax,min,
tgΨmax,min= μJ/μT·ω2max,min/2.
С другой стороны из уравне- 





ний п. 2.5.9:
ωmax,min=ωс·(1+(–)δ/2).
Таким образом, найдя Ψmax и Ψmin и проведя касательные к диаграмме энергомасс под этими углами к горизонтали (рис. 50), получим в точке их пересечения начало новой системы координат с осями Т и
J1пр, отстоящими от старых осей на искомую величину Jм и Т0пр. В целом последовательность определения Jм включает следующие операции:
Рис.
Рис. 2.38. Определение необходимого момента инерции маховика
1.Строится диаграмма Мпр(φ) для установившегося движения.
2.Строится диаграмма ∆Тпр(φ) путем графического интегрирования диаграммы Мпр(φ).
3.Строится график Jпр(φ) и диаграмма энергомасс путем исключения параметра φ из графиков ∆Тпр(φ) и Jпр(φ).
4.Определяются углы Ψmax и Ψmin, после чего находится Jм в новых координатах Тпр и J1пр диаграммы Тпр(J1пр).
Зная необходимый момент инерции маховика Jм, можно определить его максимальный диаметр D, как указано в п. 2.4.1, и массу m = 4DJ2м , после чего конструктивно подобрать ширину маховика и толщину обода.
2.6.3. Регулирование непериодических колебаний скорости движения машин
В процессе выполнения работы приходится регулировать скорость рабочего органа машины. Например, в стационарных двигателях
51

необходимо поддерживать скорость рабочего органа постоянной, а в двигателях транспортных машин эта скорость должна изменяться в широких пределах.
Из уравнения движения машины следует, что изменения скорости рабочего органа можно достигнуть за счет изменения разности работ движущих сил и сил сопротивления (Ад–Ас). Устройства, обеспечивающие изменения работы сил сопротивления, применяются в виде тормозов, например, в транспортных машинах, которые снабжаются также и приспособлениями для одновременного разобщения двигателя с машиной – орудием.
Другим способом регулирования является изменение работы движущих сил путем воздействия на орган,














 подающий энергию к
подающий энергию к
входному звену (порш-
ню у двигателя внутрен-
него сгорания, лопаткам
турбины и т. д.). Одним из них является центробежный регулятор (рис. 2.39), приводимый во вращение валом
двигателя В. Ползун А соединяется с органом, подводящим рабочее тело (пар, горючая смесь и т. д.). Регулирование может осуществляться либо человеком-оператором, либо автоматически – с помощью устройств,
называемых регуляторами.
Регулятор автоматически поддерживает скорость вала двигателя постоянной, т. к. ее увеличение приводит к уменьшению подачи рабочего тела и наоборот.
2.6.4.Уравновешивание масс в механизмах и машинах
2.6.4.1.Действие сил на фундамент. Условия уравновешивания
Вобщем случае в кинематических парах механизмов и машин возникают динамические усилия, переменные по величине и направлению. Через стойку они передаются на фундамент, вызывая дополнительные напряжения в отдельных звеньях, вибрацию и ухудшение условий работы. Чтобы этого избежать, необходимо рационально подобрать и расположить массы звеньев с условием полного или частичного гашения динамических усилий. Эта задача решается при уравновешивании.
52

Основными динамическими составляющими при работе любого механизма являются силы инерции, которые, как правило, переменны по величине и направлению. Это характерно и для случаев, когда входное звено вращается с
постоянной угловой скоростью 1 const
(рис. 2.40). Все силы и моменты сил инерции можно привести к главному вектору и моменту относительно выбранной точки:
Fи Fui ; Mи Mui Fui h Fui .
Полностью уравновешенным считается механизм, в котором Fu 0 и M u 0 , т. е.
Рис. 2.40. Положение Рис. 57 центра масс
сила давления стойки на фундамент остается постоянной при движении звеньев. Из теоретической механики известно, что Fи m a s , где m масса всех подвижных звеньев; аs ускорение центра масс системы.
Следовательно, для выполнения условия Fu 0 необходимо, чтобы аs 0 . Это равносильно требованию постоянства положения центра масс
механизма относительно стойки. Такое уравновешивание называется
статическим, или уравновешиванием первого рода. В этом случае используется метод заменяющих (сосредоточенных) масс, обладающих массой, центром масс и моментом инерции JS заменяемого твердого тела
(звена) с распределенной массой. Если поместить начало системы координат в центр масс системы, то условия эквивалентности заменяемой и заменяющих масс запишутся так:
mi m ; |
mi x i 0 ; |
mi yi 0 ; |
mi (xi2 yi2 ) JS , |
т. е. в общем случае плоского звена необходимы четыре заменяющих массы. В частных случаях число заменяющих масс может быть сведено к двум. Например, для звена АВ (рис. 1.59) можно ограничиться частичной заменой его массы m двумя массами m1 и m2, учитывая условия:
m1 m2 m ; |
m1 l1 m2 l2 0 . Отсюда: |
m1 |
m |
l2 |
; |
m2 |
m |
l1 |
. |
l |
|
||||||||
|
|
|
|
|
|
|
l |
||
Для полного уравновешивания механизма необходимо выполнение обоих условий: Fu 0 ; M u 0 , причем выполнение условия M u 0
решается при моментном (динамическом) уравновешивании, которое называется уравновешиванием второго рода.
53

2.6.4.2. Уравновешивание с помощью противовесов на звеньях механизма
Рассмотрим последовательность статического уравновешивания на примере четырехшарнирного механизма (рис. 2.41, а). Заменяем массы звеньев 1, 2, 3 сосредоточенными массами в точках A, B, C, D, причем в силу неподвижности точек A и D массы, сосредоточенные в этих точках, можно не учитывать.
а |
б |
Рис. 2.41. Уравновешивание масс:
а – до уравновешивания; б – после уравновешивания
Приведенные массы в точках В и С равны:
|
mB mB |
mB |
|
m1 |
lAS |
|
|
|
lCS |
2 ; |
|
|||||||||
|
2 |
|
1 m2 |
|
|
|
||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
lAB |
|
|
|
lBC |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
m |
|
m |
|
m |
|
m |
|
|
lBS |
2 m |
|
|
lDS |
|
|
|||||
C |
C2 |
C3 |
2 |
|
|
3 |
|
|
3 . |
|
||||||||||
|
|
|
|
|
|
|
lBC |
|
lCD |
|
|
|||||||||
Так как заменяющие массы |
|
mB |
и |
|
|
mC совершают вращательное |
||||||||||||||
|
|
|
|
|
|
|
|
|
движение, то для уравновеши- |
|||||||||||
|
|
|
|
|
|
|
|
|
вания сил инерции необходимы |
|||||||||||
|
|
|
|
|
|
|
|
|
противовесы |
|
с |
массами |
mЕ и |
|||||||
|
|
|
|
|
|
|
|
|
mF, |
|
определяемыми из условий |
|||||||||
|
|
|
|
|
|
|
|
|
(рис. 2.41, б): mE lAE mB lAB ; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
mF lDF mC lCD , где, |
задавая |
|||||||||
|
|
|
|
|
|
|
|
|
длины противовесов, |
можно |
||||||||||
|
|
|
|
|
|
|
|
|
получить их массы и наоборот. |
|||||||||||
|
|
|
|
|
|
|
|
|
Рассмотрим |
|
моментное |
уравно- |
||||||||
|
|
|
|
|
|
|
|
|
вешивание на примере четырех- |
|||||||||||
|
|
|
|
|
|
|
|
|
шарнирного |
|
|
механизма. Его |
||||||||
|
|
|
|
|
|
|
|
|
приближенное моментное урав- |
|||||||||||
|
|
|
|
|
|
|
|
|
новешивание |
|
можно осущест- |
|||||||||
Рис. 59 |
|
|
|
|
|
|
|
вить после статического уравно- |
||||||||||||
|
|
|
|
|
|
|
вешивания, введя в схему меха- |
|||||||||||||
Рис. 2.42. Моментное |
|
|
|
|
|
|
||||||||||||||
уравновешивание масс |
|
|
|
|
|
низма два одинаковых дополни- |
||||||||||||||
|
|
|
|
|
|
54 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

тельных противовеса mМ (рис. 2.42), соединенных с зубчатыми колесами
«а» и «b». Колесо «а» жестко связано с кривошипом 1 и вращается с угловой скоростью 1 , а равное ему колесо «b» вращается с той же
угловой скоростью 1 , но угловые координаты противовесов отличаются на 1800, поэтому момент пары сил инерции от противовесов mМ равен
M uМ FuМ h М.
Подбирая положение точки E, можно обеспечить направление M uМ , противоположное направлению M u , а массу противовесов mМ определяют из условия M u = M u М .
2.6.4.3. Уравновешивание вращающихся масс (роторов)
Ротором в теории балансировки называется любое вращающееся тело. В связи с появлением быстроходных машин возникла проблема уравновешивания быстровращающихся деталей. Так, например, скорость некоторых турбин, валов гироскопов, суперцентрифуг достигает 3÷50 тысяч об/мин и малейшее смещение центра масс с геометрической оси вращения вызывает появление больших сил инерции, т. е. вибрационных явлений в машине и фундаменте.
Различают статическое уравновешивание (статическая балансировка) вращающихся роторов и динамическое. Статическая балансировка достигается тем, что центр тяжести вращающейся детали переводят в неподвижную точку. Такое уравновешивание применяется для плоских деталей, длина которых мала по сравнению с диаметром. Если такую деталь заменить сосредоточенной массой m, вращающейся относительно неподвижного центра вращения (рис. 2.43, а), то можно записать уравнение динамики:
G FA Fu 0 ,
где G – сила тяжести; FA – реакция в опоре; Fu – сила инерции, равная
F m a n |
G 2 |
|
2 |
d |
а |
б |
в |
|
u |
S |
g |
|
g |
|
|||
|
|
|
|
|
|
|
||
|
|
. |
|
|
|
|
|
|
Здесь g – ускорение силы |
|
|
|
|||||
тяжести; |
d G |
дис- |
|
|
|
|||
баланс |
( lAS ), который |
Рис. 2.43. Уравновешивание плоской |
||
Рис. 60 |
||||
характеризует |
неуравнове- |
детали: а – исходная схема; б – план сил; |
||
в – установка дисбаланса |
||||
шенность |
и |
направлен так |
||
|
||||
же, как сила инерции Fu.
55

План сил в данном положении (рис. 2.43, б) показывает, что FA – величина переменная по направлению и создает динамические нагрузки и
вибрацию. Если d 0 , то |
G |
|
F |
A 0 и динамические нагрузки |
отсутствуют. Для этого необходимо уравновесить дисбаланс установкой массы противовеса с противоположной стороны (рис. 2.43, в). Тогда дисбалансы будут уравновешены, и Gп определяется из условия d dп , т.
е. G G п п , где |
п lAS . |
|
п |
Рассмотрим уравновешивание неплоской детали, которую можно представить, например, в виде двух грузов G1 и G2 (рис. 2.44, а). В этом случае возникают реакции, вызванные неуравновешенностью как сил, так и моментов от сил инерции. Причем момент от сил инерции относительно
точки А равен M u2 Fu2 |
a |
и характеризуется |
дисбалансом |
d 2 a G 2 2 a . |
|
|
|
а |
|
б |
в |
Рис. 2.44. Уравновешивание неплоской детали: а – схема; б, в – графическое определение сил тяжести и положения противовесов
В этом случае динамические нагрузки на опоры возникают, даже если проведена статическая балансировка, когда центр тяжести грузов 1 и 2 совпадает с центром вращения. Уравновешивание моментов от сил инерции вращающихся деталей будет обеспечено динамической балансировкой.
Полное уравновешивание системы можно осуществить двумя дополнительными грузами G3 и G4, установленными в разных плоскостях I
и II, называемых плоскостями исправления.
|
|
|
При этом |
|
должны |
выполняться |
условия: |
F |
ui |
0 или |
|||||||||||||||
|
|
1 |
|
2 |
|
3 |
|
4 0; |
|
|
|
|
|
|
|
|
|
|
|
||||||
d |
d |
d |
d |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
ui 0 или |
|
|
1 a1 |
|
2 |
a 2 |
|
|
3 a 3 |
|
|
4 |
a 4 0 . |
|
|||||||||
M |
d |
d |
d |
d |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
56 |
|
|
|
|
|
|
|
||

Совместное решение указанных уравнений, например, графическим путем (рис. 2.44, б, в) позволяет найти силы тяжести и положение
противовесов G3 и G4.
Балансировка вращающихся масс осуществляется на специальных балансировочных станках, при этом исключается неуравновешенность, вызванная неточностью изготовления детали.
2.6.5. Виброактивность и виброзащита машин
При работе машин с большими скоростями даже незначительные неуравновешенные массы вызывают существенные колебания и вибрацию, которые могут быть полезными, когда они вызваны целенаправленно для обеспечения технологического эффекта (вибрационные транспортеры, сита, виброударные механизмы для забивки свай и т. д.).
Например, вибрационные транспортеры обеспечивают перемещение сыпучих и кусковых материалов, заготовок и деталей на расстояния от 0,5 до 100 и более метров на заводах, мельницах, стройках, шахтах и т. д. Вибрационные транспортеры могут совмещаться с техпроцессами подогрева, охлаждения, сушки и перемешивания материалов, скорость движения по горизонтали может превышать 0,5 м/с. Грузонесущие органы вибрационных транспортеров – трубы или желоба имеют цилиндрическую или призматическую форму и совершают прямолинейно направленные или эллиптические колебания, за счет которых происходит перемещение груза (рис. 2.45).
Рис. 2.45. Схема электромагнитного вибротранспортера
57
2.6.5.1. Общие сведения об источниках колебаний и объектах виброзащиты. Колебательные процессы
В колебательной системе различают источники колебаний (И) и объекты виброзащиты (О). Например, в двигателе с ротором источником колебаний может быть ротор, а объектом виброзащиты – корпус двигателя. Силы, возникающие в связях И с О называются динамическими воздействиями. В указанном примере – это динамические реакции опор
ротора. Иногда виброактивность характеризуется не динамическим |
|||
X |
|
воздействием, а перемещением точек |
|
T |
крепления связей с источником. |
||
|
|||
|
|
Такие воздействия называется кине- |
|
|
|
матическими. Силовые и кинемати- |
|
|
|
||
ческие воздействия называются об- A0 щим термином «механические воз-
действия». Они делятся на:
а) линейные перегрузки (при  ускорении источника колебаний, например, летательных аппаратах,
ускорении источника колебаний, например, летательных аппаратах,
транспорте и т. д.); б) вибрационные воздействия,
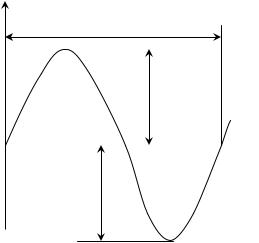
которые являются колебательными процессами гармонического вида
(рис. 2.46).
где Ao – амплитуда; o – частота; |
х(t) Ao sin( ot ), |
t – время; – начальная фаза. |
Время одного колебания называется периодом Т , который связан с частотой соотношением Т 2 / о .
Примером колебательных систем с гармоническими колебаниями являются вибрации несбалансированного ротора поршневых машин, неуравновешанных рычажных механизмов и т. д.
Более сложный вид колебательных процессов можно представить как полигармонический – в виде суммы бесконечного и конечного числа гармонических компонентов.
в) ударные воздействия – это кратковременные механические воздействия с большими усилиями. Характеризуются длительностью удара и его амплитудой, т. е. максимальным значением усилия.
Наиболее опасными являются для технических объектов вибрационные воздействия, т. к. знакопеременные нагрузки приводят к накоплению повреждений в материале и его разрушению. Вибрация вызывает у людей стойкие физиологические изменения, называемые вибрационной болезнью (ухудшение зрения, галлюцинации, нарушение координации движения).
58

Динамические воздействия, допустимые для человека, регламентируются санитарными нормами, а виброзащита является одной из важных задач современной техники.
2.6.5.2.Методы виброзащиты
Косновным методам виброзащиты, уменьшающим интенсивность колебаний объекта, можно отнести:
1.Снижение виброактивности источника, например, за счет уравновешивания, использования специальных смазок, изменения свойств материалов трущихся поверхностей (если трение в кинематических парах является причиной вибрации).
2.Изменение конструкции объекта, обеспечивающее демпфирование (гашение) колебаний и устранение резонансных явлений.
3.Динамическое гашение колебаний с применением динамических виброгасителей, которые частично уравновешивают динамические воздействия от источника колебаний.
4.Виброизоляция, включающая ослабление связей между источником
иобъектом, что уменьшает динамическое воздействие.
Демпферы, динамические гасители и виброизоляторы образуют в совокупности виброзащитные устройства, которые могут быть пассивными (без собственного источника энергии) и активными (имеющими собственный источник энергии).
Уровень виброзащиты оценивается коэффициентом эффективности виброзащиты, равным отношению какого-либо характерного параметра колебаний объекта с виброзащитой к величине этого параметра без виброзащиты.
2.6.5.3. Демпфирование колебаний
При колебаниях упругих систем происходит рассеяние энергии в окружающую среду как в узлах сочленений, так и в материале. Эти потери энергии вызваны силами неупругого сопротивления (диссипативными силами). К таким силам можно отнести силы вязкого сопротивления (в газе, жидкости), силы сухого трения и т. д.
a) |
|
б) |
|
|
|
|
F(x) |
m |
|
|
|
|
|
x |
Рис. 2.47. Демпфирующие элементы
59

Если провести циклическое деформирование упруго-диссипативного элемента (на рис. 2.47, а) например, по закону х Аcos t , то обнаружится
различие линии нагрузки и разгрузки. При этом полная составляющая сила будет равна
F (х) Fx Fq ,
где |
Fx – упругая |
составляющая |
(рис. 2.48, |
а), например, линейно |
зависимая от перемещений, Fx cx |
(с – постоянный коэффициент), где |
|||
Fq – динамическая |
составляющая от скорости |
V, коэффициента трения |
||
f тр |
и т. д. (рис. 2.48, б). |
|
|
|
Диаграмма F(x), будет иметь форму эллипса (рис. 2.48, в). Это
явление называется гистерезисом. Площадь, ограниченная петлей гистерезиса, равна энергии рассеянной за цикл. Она определяет работу диссипативных сил и влияет на амплитуду «А» циклического деформирования. Подбирая характеристики демпфера (Fq), можно обеспечить колебание системы с заданной амплитудой «А». Если такой демпфер установить в сочетании с амортизатором в виде упругого элемента (рис. 2.48, б), то можно обеспечить гашение колебаний в заданных пределах. Свойствами демпфера обладают и различные соединения (подвижные и неподвижные) за счет трения.
a) |
б) |
в) |
Fx |
Fg |
F |
x |
V,tтр |
x |
Рис. 2.48. Силовые характеристики колебательного процесса
2.6.5.4. Динамическое гашение колебаний
Метод состоит в присоединении к объекту виброзащиты (рис. 2.49, а) дополнительных устройств (динамических гасителей) с целью изменения его вибрационного состояния. Это состояние изменяется либо путем перераспределения колебательной энергии от объекта к гасителю, либо путем увеличения рассеяния энергии колебаний. В первом случае используются так называемые инерционные динамические гасители, а во втором – поглотители колебаний.
60
