
Учебная литература / ulstu2012-116
.pdf
приведения в начале цикла, то можно определить начальную |
|||||||
кинетическую энергию: Т0пр = 1/2 · J0пр · ω02. |
рассматривать |
в |
координатах |
||||
Тогда диаграмму |
энергомасс можно |
||||||
Тпр(J1пр), где ось |
J1пр |
отстоит от первоначальной оси |
Jпр |
на величину |
|||
Т0пр (рис. 30). |
|
|
|
|
|
|
|
Так как Тпр = 1/2 ·Jпр · ω2, то ω2 =2 · Тпр/Jпр =2 · μТ/μ J· tgΨ, |
где μТ и J |
||||||
– масштабные коэффициенты, используемые для построения диаграмм. |
|||||||
Таким образом, диаграмма энергомасс позволяет при установившемся |
|||||||
движении определить |
угловую скорость |
ω звена приведения в любой |
|||||
момент времени, т. е. |
ω = |
2 Т / J tg ; |
а |
tgΨ = μJ/μT·ω2/2. |
|||
M |
|
|
|
|
|
|
|
Тпр |
|
|
|
|
Тпр |
|
|
|
|
|
|
|
|
|
|
|
|
Тпрi |
|
|
|
|
Jпр |
|
|
|
|
Топр |
|
J1пр |
|
Jпр |
|
|
|
|
i |
|
|
|
Jiпр |
|
|
|
45 |
|
|
|
|
|
|
|
|
||
|
|
|
.27 |
|
|
|
|
|
|
|
Рис. 30 |
|
|
|
|
|
Рис. 2.17. Построение диаграммы энергомасс |
|
|||||
2.2.7. Определение реакций в кинематических парах (силовой расчет)
Зная активные силы, действующие на звенья механизма и силы инерции этих звеньев, можно произвести его кинетостатический расчет, т. е. определить реакции в кинематических парах и уравновешивающую силу (момент) на входном звене, причем эта сила (момент) является движущей при совпадении ее направления с направлением движения входного звена или силой (моментом) сопротивления, если ее направление противоположно этому движению. При кинетостатическом расчете реакции в кинематических парах определяются путем статического расчета, который базируется на результатах кинематического анализа, включая ускорения, необходимые для определения сил (моментов) инерции.
31

При силовом расчете используется принцип Даламбера, позволяющий решение задачи динамики свести к статическому расчету. Согласно этому принципу приведение ускоренно движущейся системы в равновесие обеспечивается условным приложением к этой системе сил инерции. При этом неизвестные силы определяются из уравнений статики.
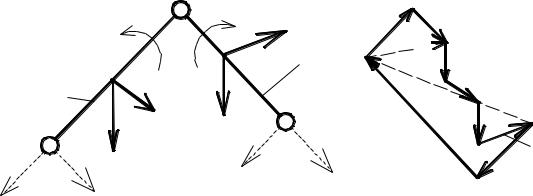
Силы взаимодействия между звеньями (реакции) можно считать направленными по нормали к контактирующим поверхностям, если расчет ведется без учета сил трения (рис. 2.18, а, б).
При графоаналитическом решении используется метод плана сил. Механизм расчленяется на структурные группы Ассура и начальные звенья. Расчет ведется, начиная с последней структурной группы, и заканчивается расчетом входного звена.
а) |
б) |
При расчете струк- |
|||||
|
|
турных |
групп |
к |
ним |
||
|
|
прикладываются |
все |
||||
|
|
действующие |
|
силы, |
|||
|
|
включая силы инерции |
|||||
|
|
и реакции |
отброшен- |
||||
|
|
ных |
связей. |
Каждая |
|||
|
|
из |
неизвестных реак- |
||||
|
|
ций, |
при |
необходи- |
|||
Рис. 31 |
|
мости, может быть раз- |
|||||
Рис. 2.18. Реакция в кинематических парах: |
|||||||
Рис. 31. Реакции в кинематических парах |
ложена |
на |
две |
сос- |
|||
а – цилиндрический шарнир; |
б – поступательная пара |
||||||
|
|
тавляющие по выбран- |
|||||
ным направлениям, например, вдоль оси звена (нормальная Fn) и |
|||||||
перпендикулярно оси (тангенциальная Ft). При равенстве числа уравнений |
|||||||
статики числу неизвестных реакций их можно определить аналитически и |
|||||||
графически, построив многоугольник (план) сил. Неизвестные определятся |
|||||||
из условия замкнутости векторной суммы сил. |
|
|
|
|
|
|
|
32
|
а) |
|
|
B |
M и2 |
б) |
t |
|
|
|
|
M и1 |
|
|
|
Fn |
|
|
|||
|
|
|
|
Fi,1 |
|
|||||
|
|
|
|
|
|
|
i,1 |
F |
|
|
|
S |
|
|
S2 |
Fи2 |
2 |
|
i,1 |
G1 |
|
|
1 |
Fи1 |
|
|
|
|||||
|
1 |
G2 |
|
C |
|
Fj,2 |
F |
|
||
|
|
|
|
|
и1 |
|
||||
F |
G1 |
|
|
|
|
|
n |
Fn |
G |
|
|
|
|
|
|
|
Fj,2 |
j,2 |
2 |
Fи2 |
|
|
|
|
t |
|
t |
|
|
|
Ft |
|
Fn |
|
Fi,1 |
|
|
|
|
j,2 |
|
||
|
|
Fj,2 |
|
|
|
|
|
|||
i,1 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.19. Силовой расчет двухповодковойРис. 32.33 |
ассуровой группы |
|
|||||||
|
|
|
1-го вида: а – схема; б – план сил |
|
|
|
||||
Рассмотрим примеры:
1) Двухповодковая группа с вращательными парами:
Fi,1t определяется из уравнения моментов для звена 1 – ∑МB = 0 относительно т. В. (рис. 2.19, а);
Fj,2t определяется из уравнения моментов для звена 2 – ∑МВ = 0 относительно т. В (рис. 2.19, а).
При отрицательных значениях реакций необходимо изменить их направления на противоположные.
Fi,1n и Fj,2n определяются из плана сил (рис. 2.19, б), полученного на основе векторного уравнения;
∑Fk=0, где Fk – силы, действующие на структурную группу.
33

2) Двухповодковая группа шатун-ползун (рис. 2.20, а, б)
аа) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бб) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 33 Рис. 2.20. Силовой расчет двухповодковой группы
шатун-ползун: а – схема; б – план сил
определяется из уравнения моментов – ∑МА = 0 относительно т. А.
F i,1 = F i,1n + F i,1t определяется из плана сил (рис. 2.20, б) на основе векторного уравнения ∑Fk=0.
3) Двухповодковая группа кулиса-камень (рис. 2.21, а)
а |
Fi,2 |
B |
F |
|
б |
|
в |
|
|
|
|
|
|||||
а) |
|
|
|
|
б) |
|
в) |
|
|
Fи1 |
|
Mи1 |
Fi,2 |
F1,2 |
Fn |
Fi,1t |
F |
|
|
G1 |
|
i,1 |
|
G1 |
||
|
|
|
|
|
Fi,2 |
|||
|
A |
|
|
|
|
|
F и1 |
|
|
|
|
|
|
|
|
||
Fi,1n |
|
F t |
|
|
|
|
|
|
|
|
i,1 |
|
|
. 34 |
|
|
|
|
|
|
|
|
Рис.35 |
|
|
|
|
|
|
Рис. 2.21. Силовой расчет двухповодковой |
|
||||
|
|
группы кулиса-камень: а, б – схемы; в – план сил |
||||||
Fj,2 определяется из уравнения моментов – ∑МА = 0. Fi,1=Fi,1n+Fi,1t определяется из плана сил (рис. 2.22, в), на основе векторного уравне-
ния ∑Fk = 0. При этом особенность расчета данной группы Ассура состоит в возможности некоторого упрощения вычислений в случае, когда весом
34
камня 2 можно пренебречь. Тогда реакция Fi,2 противоположна реакции F1,2 и перпендикулярна АВ, т. е. линия ее действия известна (рис. 2.21, б).
4) Входное (начальное) звено (рис. 2.22, а)
а) |
Fj,1 |
A |
F и1 |
|
б) |
|
|
|
|
|
|
Fj,1 |
|
|
M ур |
Mи1 |
|
|
Fj,1n |
|
|
|
|
Ft |
|||
|
G1 |
|
G1 |
|
||
|
|
|
|
|
j,1 |
|
|
O |
|
|
|
|
F и1 |
Fj,1n |
|
Fj,1t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. 35 |
|
|
механизма: |
|
Рис. 2.22. Силовой расчетРиспервичного.36 |
|||||
|
а – схема; б – план сил |
|
|
|
||
Мур определяется из уравнения моментов – ∑Мо = 0. F j,1 = F j,1n + F j,1t определяется из плана сил (рис. 2.22,б) согласно векторному уравне-
нию ∑F k = 0.
2.2.8. Теорема Жуковского о жестком рычаге
Одним из способов определения приведенной силы Fпр является способ, предложенный проф. Н. Е. Жуковским. Уравнение, из которого
может |
быть |
найдена |
|
Fпр, |
а) |
б) |
основано на равенстве мощностей: |
||||||
F∑пр·VA·cos(F∑пр |
|
|
|
|
||
VA)=∑Fi·Vi·cos(Fi Vi). |
|
|
|
|
||
Рассмотрим |
какое-либо |
|
|
|||
звено |
механизма, |
в |
т. |
|
|
|
В которого приложена сила Fi |
|
|
||||
под углом αi к вектору скорости |
|
|
||||
Vi этой точки (рис. 2.22, а). |
|
Рис. 36 |
||||
Мощность, развиваемая |
|
силой |
|
|||
Fi, равна: |
Pi= Fi · Vi· cosαi. |
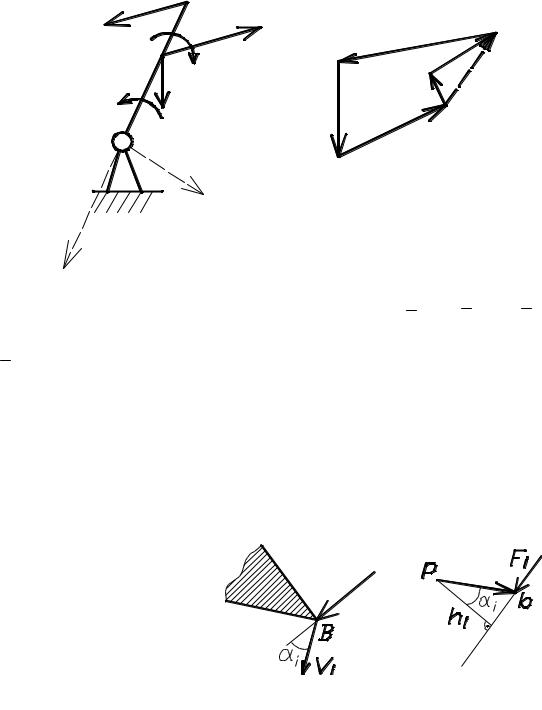
Рис. 2.23. Построение рычага Жуковского: |
Если вектор скорости т. В |
а – схема; б – перевернутый план скоростей |
|
(план скоростей) повернуть на |
|
|
90˚ и |
силу Fi приложить к |
концу вектора (в т. «b»), сохранив ее |
|
|
35 |

направление, то момент этой силы относительно полюса «p» будет равен
(рис. 2.23, б):
Mi = Fi · hi = Fi · Vi · cosα i= Pi,
т. е. равен мощности силы Fi. Таким образом, Fi можно найти, повернув на 90˚ план скоростей и приложив к нему все внешние силы, включая силы инерции в соответ-ствующих точках и сохраняя их направления. Тогда из
уравнения моментов такого рычага: F∑пр·hпр=∑Fi·hi, получим:
F∑пр=∑Fi·hi/hпр,
где hi и hпр – кратчайшие расстояния от полюса плана скоростей до линии действия i-й и приведенной сил. Повернутый на 90° план скоростей с приложенными к нему силами называется жестким рычагом Жуковского.
Величина Fпр, или Мпр, зависит от положения механизма, поэтому можно построить диаграмму, например, Fпр(φ), являющуюся функцией положения звена приведения. Для этого необходимо последовательно определить значения Fпр методом рычага Жуковского для целого ряда положений механизма в пределах цикла (F1пр, F2пр,…) и отложить их на диаграмме (рис. 2.24).
Fпр
F1пр F2пр




 1
1 



 2
2
Рис.26
. 37
Рис. 2.24. Годограф приведенной силы
Приведенная сила F∑пр, или момент М∑пр, характеризует реакцию механизма на движение его входного звена по определенному закону, задаваемому двигателем. Сила или момент, равные по величине приведенной силе или моменту, но противоположные им по направлению,
называются уравновешивающей силой Fур, или моментом Мур. Эта сила,
или момент, развивается двигателем и обеспечивает заданное движение входного звена.
Если к рычагу Жуковского приложить все внешние силы, включая силы инерции, а также Fур, то его можно рассматривать в равновесии, из условия которого Fур· hур + ∑Fi · hi = 0 можно определить неизвестную Fур, а также найти мощность двигателя Pдв, требуемую для получения заданного движения входного звена в заданном положении
Pдв = Fур· VA· cos (Fур,VA )= Mур· ω.
36

2.2.9. Особенности учета сил трения при силовом расчете рычажных механизмов
Для учета сил трения в кинематических парах рычажных механизмов при определении Fур или M ур используется метод приведения сил трения,
позволяющий определять уточненные значения F* ( M* ) без повторного
ур ур
силового расчета с учетом трения по формуле
M*ур Мур Мпртр ,
где M ур– уравновешивающий момент, вычисленный без учета трения;
Мпртр – момент трения, приведенный к вращающемуся с угловой скоростью
в входному звену, и равный:
Мтр Piтр . пр в
Здесь Рiтр – суммарная мощность сил трения в кинематических парах.
Для определения реакций в кинематических парах с учетом трения обычно используется метод последовательных приближений, когда по найденным без учета трения реакциям определяются силы и моменты трения в кинематических парах. Затем эти силы прикладываются как внешние и производится перерасчет реакций в установленном порядке. Обычно достаточно одного перерасчета (итерации).
2.3.Основные критерии работоспособности
ирасчета деталей машин
При проектировании деталей машин к ним предъявляются многие требования (критерии работоспособности и расчета), иногда противоречивые. Рассмотрим основные из них.
2.3.1. Прочность
Суть этого требования состоит обычно в том, что напряжения не должны превышать допускаемых величин и не должно быть остаточных деформаций. Различают расчеты на сопротивление усталости (когда учитываются часто повторяющиеся и длительно действующие нагрузки) и расчеты на сопротивление пластическим деформациям (когда учитываются максимальные кратковременные перегрузки).
37
2.3.2. Жесткость
Упругие деформации не должны превышать допустимых величин (удлинения, прогибы, углы закручивания и т. п.).
2.3.3. Виброустойчивость
Способность конструкции работать в нужном диапазоне режимов без недопустимых колебаний. Чаще всего расчеты ведутся на недопущение резонанса. Иногда ограничиваются амплитуды колебаний. Шумы при работе машины ограничиваются санитарными нормами.
2.3.4. Износостойкость
Большинство деталей выходит из строя из-за изнашивания. Различают такие виды изнашивания, как механическое (особую роль играет абразивное), молекулярно-механическое (схватывание, или заедание, когда при высоких температурах и давлениях частицы материала могут быть вырваны из одной детали и прилипнуть к другой) и коррозионномеханическое (когда после ржавления частицы материала механически стираются, а затем ржавеет следующий слой).
Практические расчеты обычно ведутся на ограничение удельного давления на поверхности трения. Особый случай – расчеты на жидкостное трение для подшипников.
2.3.5. Теплостойкость
Нагрев деталей может вызвать понижение прочности, увеличение изнашивания, заклинивание, заедание, понижение точности работы машины. Составляются уравнения теплового баланса, из которых можно определить рабочую температуру и сравнить ее с допускаемой для данной смазки. Иногда требуется вводить искусственное охлаждение.
2.3.6. Надежность
Надежностью называется свойство изделий выполнять в течение заданного времени свои функции, сохраняя в заданных пределах эксплуатационные показатели. Надежность обусловливается безотказностью, долговечностью, ремонтопригодностью и сохраняемостью.
Безотказность – свойство сохранять работоспособность в течение заданной наработки (ресурса) без вынужденных перерывов. Утрата работоспособности называется отказом. Различают отказы полные и
38
частичные, внезапные и постепенные, устранимые и неустранимые, приработочные и износовые.
Основной показатель – вероятность безотказной работы в течение заданного времени.
Вероятность безотказной работы системы равна произведению вероятностей безотказной работы отдельных элементов. Пусть число элементов n = 10; вероятности Р1 = Р2 … Р10 – 0,9. Тогда вероятность безотказной работы системы Р = 0,910 ≈ 0,35.
Долговечность – свойство изделия сохранять работоспособность до предельного состояния с необходимыми перерывами для ремонтов и технического обслуживания. Основной показатель – нормативный срок службы изделия.
Ремонтопригодность – приспособленность изделия к предупреждению, обнаружению и устранению отказов путем проведения технического обслуживания и ремонтов.
Сохраняемость – свойство изделия сохранять требуемые эксплуатационные показатели после установленного срока хранения и транспортировки.
Существует теория надежности, основанная на методах теории вероятности и математической статистики.
2.3.7. Технологичность
Она сводится к минимальной трудоемкости изготовления изделия с учетом программы выпуска. Форма детали должна соответствовать выбранному способу изготовления (литье, штамповка, сварка, обработка резанием или комбинированный вариант), установленному совместно конструктором и технологом.
2.3.8. Точность механизмов
На точность работы нового механизма влияют следующие основные факторы:
1)Технологически неизбежные отклонения в размерах и форме деталей, регламентируемые системой допусков.
2)Упругие деформации звеньев под влиянием действующих сил (необходим расчет на жесткость).
3)Температурные деформации звеньев (особенно при неравномерном нагреве).
4)Относительные смещения деталей под действием сил за счет неплотности и деформаций в соединениях.
39

5) Смещение звеньев за счет зазоров и толщины слоев смазки в кинематических парах.
Дополнительные факторы, влияющие на точность механизма, находящегося в эксплуатации:
1.Износ трущихся деталей.
2.Остаточные деформации деталей (особенно смятие в соединениях).
3.Постепенное деформирование деталей (коробление) за счет остаточных напряжений при технологических процессах, связанных с
нагревом до высоких t .
Идеальным механизмом называется механизм с абсолютно точными размерами всех звеньев.
Первичные ошибки – ошибки в основных размерах и форме звеньев. Они делятся на:
1)Систематические (постоянные или изменяющиеся по определенному закону).
2)Случайные (их величину нельзя заранее предугадать).
3)Грубые – недопустимо большие ошибки, подлежащие устранению. Ошибкой положения механизма называется разница положений
ведомых звеньев действительного и идеального механизмов при одинаковых положениях ведущих звеньев.
Ошибкой перемещения механизма называется разница перемещений ведомых звеньев действительного и идеального механизмов при одинаковых положениях ведущих звеньев.
Ошибками скоростей и ускорений механизма называются разности между скоростями и ускорениями ведомых звеньев действительного и идеального механизмов при одинаковых положениях ведущих звеньев.
Динамическими ошибками механизма называется разность сил реакций в действительном и идеальном механизмах при одинаковых положениях ведущих звеньев.
Для нахождения ошибок положения механизма по первичным ошибкам существует принцип независимости первичных ошибок, положенный в основу графического способа их нахождения. Он состоит в построении планов малых перемещений.
Рассмотрим, например, кривошипно-шатунный механизм. В нем возможны следующие ошибки, влияющие на перемещение ползуна
(рис. 2.25, а):
1) Ошибка в длине шатуна 2 – q2 .
Строим план малых перемещений. Дугу приближенно заменяем перпендикуляром к шатуну АВ и определяем ошибку x2 (рис. 2.25, б).
2) Ошибка в длине кривошипа ОА – q1 (рис. 2.25, б).
40
