
Учебная литература / ulstu2012-116
.pdf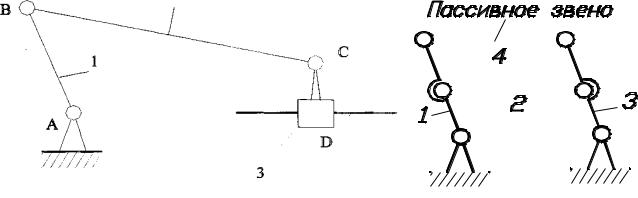
W = 6n –5p5 – 4p4 – 3p3 – 2p2 –р1. |
(1) |
Так как любой механизм имеет одно неподвижное звено |
(стойку) и |
«п» подвижных звеньев, то формула (1) может использоваться для
определения W пространственного механизма, где |
n – число подвижных |
|
звеньев, a W – степень подвижности механизма, |
показывающая, сколько |
|
нужно |
иметь ведущих звеньев (двигателей) для получения определенного |
|
движения остальных его звеньев; q – число повторяющихся связей.
Для плоского механизма степень подвижности определяется по формуле
Чебышева: |
|
W = 3n – 2p5 – p4, |
(2) |
Приэтомк.п. 5-гоклассасуществуетввидепоступательных, вращательныхи винтовых. Например, кривошипно-ползунный плоский механизм (рис. 7), в
котором n = 3; р5 = 4; P4 = 0, имеетW=3·3–2·4–0 = l.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8 |
|
|
|
|
|||||||||||||||||||||||||||||
Рис 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Рис. 1.8. Механизм |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Рис. 1.7. Кривошипно-ползунный |
|
|
|
|
|
|
|
|
|
|
параллелограмма |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
механизм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
При определении W необходимо учитывать возможность наличия так называемых «пассивных» звеньев, т. е. звеньев, устраняемых безформального ущербадлякинематикианализируемогомеханизма(рис. 1.8):
а) W=3·4–2·6–0=0 – с пассивным звеном, б) W=3·3–2·4–0=1 – фактически.
Кроме того, необходимо учитывать возможность наличия избыточных связей, которые не реализуются в реальном механизме, а их число q определяется разностью между числом связей в к. п. действительного и формально возможного механизмов.
На рис. 1.9, а показан действительный механизм, а на рис. 1.9, б – формально возможный механизм, имеющий функциональное назначение, аналогичное действительному механизму, но где все связи, в отличие от действительного механизма, реализованы.
11

p4 |
=0, p 5а=3 . |
p4l |
= 1, pб5l |
= 2. |
|
|
Рис.9 |
|
|
Рис. 1.9. Клиновые механизмы: а – действительный; б – формально возможный
Число избыточных связей q в действительном механизме равно: q = (2p5+p4) –(2p/5+p/4)=(2·3+0) –(2·2+1)=1,
т. е. степень подвижности действительного механизма равна: W = 3n–2p5–p4+q=3·2–2·3 – 0+1=1.
Вобщемслучаепространственногомеханизма: W = 6n– i ·pi + q (i от1 до5).
1.4. Классификация механизмов
Основной принцип образования рычажных механизмов был сформулирован в1914 годупрофессором Л. В. Ассуроми заключается в следующем. Схема любого механизма может быть составлена последовательным присоединением к входным (начальным) звеньям и стойке к.ц. с нулевой степенью подвижности. Такие к. ц. называются структурными группами Ассура. ПримерыразличныхгруппАссурапоказанынарис.1.10.
2-х поводковая группа Ассура 2-го класса 2-го порядка
W =3 2-2 3=0
3-х поводковая группа Ассура
3-го класса, 3-го порядка
W =3 4-2 6-0=0
Группа Ассура 4-го класса 2 -го порядка
W = 3 4-2 6-0= 0
Рис.10
Рис. 1.10. Ассуровы группы
12

Начальное звено со стойкой образует простейший механизм 1-го класса |
|||||
(рис. 1.11). |
|
|
|
|
|
Путем присоединения к таким механизмам |
|
||||
различных групп Ассура можно получить механизм |
|
||||
любой сложности. ГруппыАссураклассифицируются |
|
||||
по числу к.п., которыми они присоединяются к |
|
||||
основномумеханизму. Эточислоопределяетпорядок |
|
||||
группы. |
|
|
|
класс, |
Рис. 1.11. Простейшие |
Кроме того, группа Ассура имеет |
механизмы 1-го класса |
||||
определяемый числом к. п., образующих наиболее |
|
||||
сложныйзамкнутыйконтур. |
|
|
|
|
|
Состав и последовательность присоединения групп Ассура в |
|||||
механизме можно выразить его формулой строения. Механизм в целом |
|||||
классифицируется по группе наивысшего класса. |
|
||||
На рис. 1.12 показан пример такой классификации: |
|||||
Формула строения механизма 1(1,6) 2(2,3) 2(4,5). |
|||||
2 |
3 |
5 |
|
|
|
|
6 |
|
|
||
|
|
|
|
|
|
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
группы Ассура 2-го |
|
|
механизм 1-го |
|
класса 2-го порядка |
|
|
|
|
класса |
|
|
|
Формула строения механизма |
||||
|
Рис. |
.12. Формула строения механизма |
|||
|
1(1,6) |
2 (2,3) |
2 (4,5) |
|
|
|
|
1(1,6) |
2(2,3) 2(4,5) |
|
|
|
|
Рис.12 |
|
|
|
Среди всего многообразия различают рычажные, кулачковые, фрикционные, зубчатые механизмы, механизмы с гибкими звеньями (например, ременные передачи) и другие виды. Менее распространенные классификации подразумеваютналичиемеханизмовс низшими иливысшимипарамивплоском илипространственномисполнении и т. д.
Учитывая возможность условного превращения практически любого механизма с высшими парами в рычажный, в дальнейшем наиболее подробно рассматриваютсяименноэтимеханизмы.
Среди рычажных механизмов наиболее распространены так называемые четырехзвенные, примеры которых представлены на рис. 1.13, а-г. В этих механизмах встречаются однотипные звенья: кривошип – звено, совершающее
13
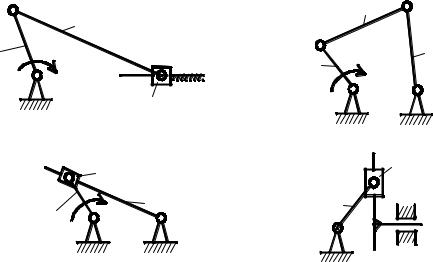
полнооборотное вращательное движение вокруг неподвижной оси; коромысло – звено, совершающее неполнооборотное вращательное движение вокруг неподвижной оси; ползун – звено, совершающее поступательное движение относительно стойки; камень – звено, совершающее поступательное движение относительно подвижной направляющей, называемой кулисой; шатун – звено, совершающееплоскопараллельное движение.
а |
|
|
в |
б |
г2 |
|
1 |
|
2 |
|
3 |
||
|
|
|
|
1 |
||
|
|
|
|
|
|
|
|
|
|
3 |
4 |
|
4 |
|
|
|
|
|
||
|
в |
|
|
г |
|
|
|
|
|
|
|
||
|
|
Рис. 13. Виды рычажных механизмов: а - кривошипно- |
|
|||
|
|
|
2 |
|
2 |
|
|
|
ползунный; б –3четырехшарнирный; в – кулисный; г – |
|
|||
|
|
1 |
|
|
1 |
|
|
|
|
4 |
|
3 |
4 |
Рис. 1.13. Виды рычажных механизмов: а – кривошипноползунный; б – четырехшарнирный; в – кулисный; г – синусный
Контрольные вопросы
1.Что называется механизмом?
2.Что называется машиной?
3.По каким признакам классифицируются механизмы?
4.Какие звенья называются начальными, ведущими, ведомыми, входными, рабочими, пассивными, выходными?
5.Какие звенья получили названия: кривошип, шатун, кулиса, камень, коромысло, ползун?
6.Как изображаются на кинематических схемах звенья механизма?
7.Что называется кинематической парой?
14
8.По каким признакам классифицируются кинематические пары?
9.Какая кинематическая пара называется высшей?
10.Какая кинематическая пара называется низшей?
11.Какими преимуществами и недостатками обладают высшие и низшие кинематические пары?
12.Каким образом кинематические пары классифицируются по числу условий связи?
13.Что называется планом механизма?
14.Что называется степенью подвижности механизма?
15.Что показывает формула Чебышева П. Л.?
16.Сколько степеней подвижности у механизма первого класса?
17.Что называется кинематической цепью?
18.Как классифицируются кинематические цепи?
19.Какая кинематическая цепь называется замкнутой?
20.Каким образом кинематическая цепь преобразуется в механизм?
21.Что называется структурной группой?
22.Как определяется класс и порядок структурной группы по Артоболевскому И. И.?
23.Как записывается формула строения механизма?
24.Что такое избыточная связь в механизме?
2.РЫЧАЖНЫЕ МЕХАНИЗМЫ
2.1. Кинематический анализ
Кинематический анализ механизмов включает вопросы изучения звеньев с геометрической точки зрения, т. е. без учета действующих сил. Для этого используется графические, аналитические и экспериментальные методы исследования.
Одним из наглядных методов является графоаналитический, который включает:
а) построение планов положения механизма; б) определение скоростей и ускорений характерных точек или звеньев механизма.
При графических построениях на чертеже изображаются длины звеньев, скорости, ускорения и другие величины в определенном масштабе, характеризуемом масштабным коэффициентом: = значение
параметра/длина отрезка.
Например, вектор длиной 10 мм изображает скорость V = 20 м/с.
Тогда v = 20/10 = 2 м ·с-1/мм.
15
2.1.1. Построение планов положения механизма
Графическое изображение взаимного расположения звеньев механизма, соответствующее заданному моменту времени, называется планом положений, или планом механизма. Планы положения строятся в определенном масштабе методом
|
засечек |
в |
соответствии с |
||||
|
формулойстроениямеханиз- |
||||||
|
ма, при этом должны быть |
||||||
|
заданы |
линейные |
размеры |
||||
|
всехзвеньев(рис. 2.1). |
|
|||||
|
После |
построения |
нес- |
||||
|
кольких |
совмещенных |
пла- |
||||
А1 |
нов механизма при необхо- |
||||||
димости |
можно |
определить |
|||||
Рис. 2.1. Планы положений механизма |
графически |
траектории |
ха- |
||||
рактерных |
точек |
звеньев, |
|||||
Рис. 14 |
|||||||
|
имеющих |
сложное |
движе- |
||||
|
ние, например, |
центра тя- |
|||||
|
жестиS шатунаАВ(рис. 2.1). |
||||||
2.1.2. Определение скоростей и ускорений механизма методом планов
Метод планов является одним из самых наглядных. Определению подлежат линейные скорости и ускорения отдельных точек и угловые скорости и ускорения звеньев. При этом предварительно составляются векторные уравнения для скоростейиускоренийточекзвеньев, совершающихсложноедвижение, например:
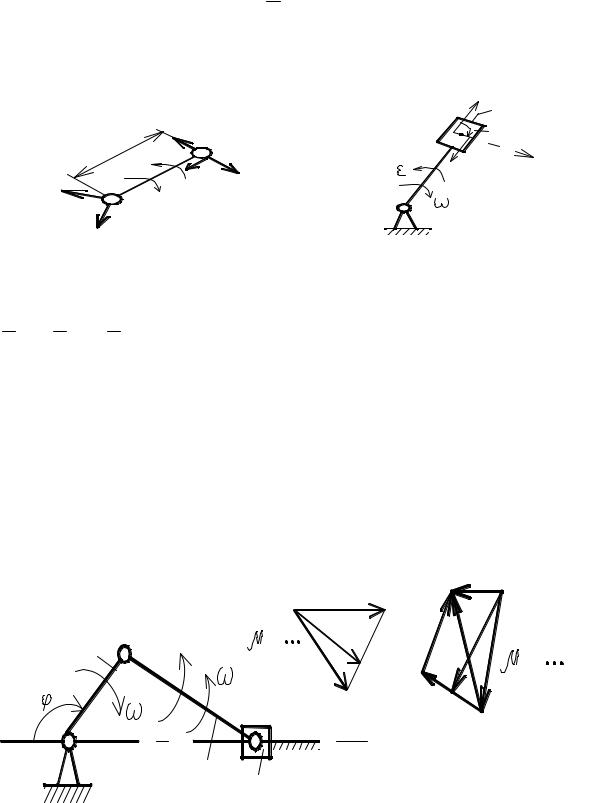
а) звено совершает плоско-параллельное движение, состоящее из переносного, т. е. поступательногососкоростьюполюсаиотносительноговращательноговокруг полюса(рис. 2.2).
Принимаязаполюст. А, получим: VВ VА VВА ; гдеVВА= ·1АВ;
аВ аА аВА ; где аВА аВАn аВАt ; при аnВА = 2·1АВ; аtВА = ·1АВ. Здесь V,a,
, – линейные скорости и ускорения соответствующих характерных точек, а также угловые скорость и ускорение звена (индексы соответствуют характеру ускоренийиобозначениямточек);
б) звено совершает сложное движение, состоящее из переносного вращательногоиотносительногопоступательного, например, звена1 (рис. 2.3).
16
|
|
|
|
|
|
|
V B |
1 B 2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
l |
B A |
|
a Bt |
A |
|
|
|
B |
|
|
|
1 |
k |
B |
|
|
|
|
|
|
|
|
|
|
a B 1 B 2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
V |
|
|
|
|
a t B |
|
B |
|
|
|
|
A |
|
a nB A |
B A |
|
|
|
|
1 |
|
2 |
|
|
V A |
|
|
|
|
|
|
|
|
|
|
|
|
|
a A |
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис с15. 5 |
|
|
|
|
|
|
Р и с . 1 6 |
|||||
Рис. 2.2. Плоско-параллельное |
Рис. 2.3. Сложное движение звена |
||||||||||||
|
движение звена |
|
|
|
|
|
|
|
|
|
|
||
Пусть В1 |
и В2 – |
точки, |
принадлежащие |
звеньям 1 |
|
|
и |
2. Тогда: |
|||||
V В1 V В2 |
V В1В2 ; |
|
где VВ2 = |
·1АВ . аВ1 |
=аВ2 |
аВt |
1А2 |
аВК1В2 , где ускорение |
|||||
Кориолиса аkВ1В2 = 2VВ1В2 · и совпадает с направлением вектора VB1В2, повернутогона90° всторонупереносноговращения.
Решениевекторныхуравненийосуществляетсяграфическипутемпостроения такназываемыхплановскоростейиускорений, накоторыхабсолютныескорости и ускорения откладываются от одной точки, называемой полюсом, в определенноммасштабе.
Пример расчета кривошипно-ползунного механизма рассмотрен на рис. 2.4, гдепланположений– а), планыскоростейиускорений– б, в).
|
|
|
|
б)планскоростей |
в)планускорений |
|||
|
а)планположений |
|
б |
|
|
в |
|
|
|
|
а |
|
|
в |
в |
П |
|
|
|
А |
|
Р |
|
|||
|
1 |
E |
= |
|
|
|
|
|
|
S |
|
|
|
|
|||
|
|
|
|
V |
S |
n |
|
= |
|
|
|
|
2 |
a |
|||
|
|
|
|
|
|
|
||
|
|
|
|
а |
S |
|
|
|
|
|
1 |
|
В |
а |
|
||
|
|
|
|
|
||||
Х |
О |
|
2 |
4 |
Х |
|
|
|
|
|
|
3 |
|
|
|
|
|
РисРис. .17
Рис. 2.4. Планы: а – положений; б – скоростей; в – ускорений
17

Векторные |
|
|
уравнения |
для |
|
скоростей |
записываются |
|
в |
|
|
виде: |
||||||||||||||||||||||||||||||
|
|
В |
|
А |
|
ВА ; |
|
В |
|
Вх |
|
|
|
; |
где VA= 1 · lOA; |
|
Вх 0 ; |
|
|
ВА_|_AB; |
||||||||||||||||||||||
|
V |
V |
V |
V |
V |
V |
V |
V |
||||||||||||||||||||||||||||||||||
|
ВВх |
|||||||||||||||||||||||||||||||||||||||||
|
|
ВВх||x-x, |
|
|
т. е. |
|
в |
выбранном |
|
масштабе |
μV: pb||x-x; |
|
|
|
_|_ |
|
; VBA= |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
аb |
АВ |
|||||||||||||||||||||||||||||||||
|
V |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
μV · ab; |
VB = μV · pb |
|
Vs v PS и |
2 = VBA/ lAB. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
Векторные уравнения для ускорений при 1 = const записываются в |
||||||||||||||||||||||||||||||||||||||
виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а |
В |
а |
А |
а |
ВА |
; |
|
|
|
а |
В |
а |
Вх |
аk |
аt |
; |
где |
|
а |
А |
аn |
2 |
1 |
; |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВВх |
ВВх |
|
|
|
|
|
|
|
А |
|
|
|
1 |
ОА |
||||||||||||
аВА аВАn |
аВАt |
; здесь |
anBA= 22 · lAB; atBA = ε2 · |
lAB; aBx=0; |
akBBx=0; |
|||||||||||||||||||||||||||||||||||||
аtBBx||x-x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Все ускорения представлены в выбранном масштабе |
|
|
а |
в |
виде |
|||||||||||||||||||||||||||||||||||||
соответствующих отрезков, например, aB |
= μa |
· πb |
|
|
|
и |
|
|
т. |
д. |
||||||||||||||||||||||||||||||||
При определении скоростей и ускорений промежуточных точек звеньев, |
||||||||||||||||||||||||||||||||||||||||||
например т. |
S, можно использовать так называемую теорему подобия, |
|||||||||||||||||||||||||||||||||||||||||
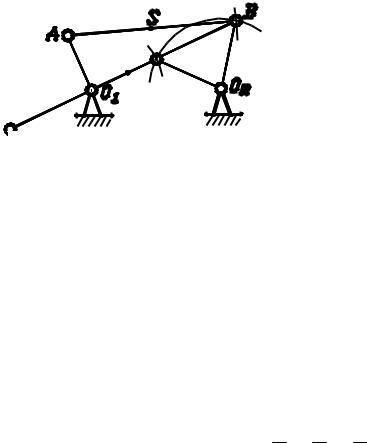
согласно которой точки на плане положений звеньев и соответственные точки на планах скоростей и ускорений образуют подобные фигуры или пропорциональные отрезки. Рассмотрим доказательство данной теоремы. На рис. 2.5 показано звено АBC и планы скоростей и ускорений для точек
этого |
звена: |
отрезок |
на плане скоростей |
соответствует |
|
СА _|_ СА; |
|||||||||||
V |
|||||||||||||||||
отрезок ab на плане скоростей соответствует |
|
|
АВ_|_ |
|
; отрезок bc на |
||||||||||||
|
|
АВ |
|||||||||||||||
|
V |
||||||||||||||||
плане |
скоростей соответствует |
|
ВС_|_ |
|
; |
|
т. |
е. треугольник abc |
|||||||||
|
ВС |
|
|||||||||||||||
V |
|
||||||||||||||||
подобен треугольнику ABC. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ускорения относительного (вращательного) |
|
движения равны: |
|||||||||||||||
a CA lCA |
( 4 2 ) ; a AB lAB |
( 4 2 ) ; |
a BC lBC |
( 4 2 ) , |
|||||||||||||
т. е. aCA/ lCA =aAB/ lAB =aBC/ lBC |
или |
ca/CA=ab/AB=bc/BC. |
|
|
|||||||||||||
Следовательно, треугольник abc подобен треугольнику ABC. |
|||||||||||||||||
Аналогичным является |
построение |
фигур для |
любой промежуточной |
||||||||||||||
точки, |
например т. S (рис. 2.5, а, б, с). |
|
|
|
|
|
|
|
|
||||||||
18

a)аа) |
|
б |
б) |
в |
|
|
A |
B |
Планскоростей Планускорений |
||||
c |
a |
c |
|
a |
||
S |
|
s |
||||
|
s |
P |
|
b |
||
C |
|
|
b |
П |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
а) звено |
|
Рисб) план.18скоростей |
с) план ускорений |
|||
|
|
|
|
|||
Рис. 2.5. Планы: а – звено; б – скоростей; в – ускорений
2.1.3. Исследованиерычажныхмеханизмовметодомкинематическихдиаграмм
Кинематическойдиаграммойназываетсяграфическаязависимостькакого-либо параметра движения звена от времени или от перемещения входного звена, представленныевопределеннойсистемекоординат.
Еслиизвестнаоднакинематическаядиаграмма, томожно получить остальные зависимостипутемграфическогодифференцированияилиинтегрирования.
На рис. 1.19, а, б показана последовательность построения кинематической диаграммыперемещенияползунакривошипно-ползунногомеханизма S( ) и S(t), а также элементы графического дифференцирования с получением диаграммы скоростей V(t) методом хорд. Если диаграмма V(t) первична, то процесс, обратный дифференцированию, обеспечивает получение диаграммы S(t) и называется графическим интегрированием. Следует отметить, что графические методы частоприводяткискажениямрезультатов из-за неточности графических построений, поэтому необходимо контролировать
расположениехарактерныхточек, соответствующихэкстремумамнадиаграммах.
2.1.4. Кинематическоеисследованиерычажныхмеханизмованалитическим методом
Аналитические методы исследования позволяют проводить анализ с заданной степенью точности. Кроме того, создание математических моделей механизмов позволяетрешатьзадачиихоптимальногосинтезаприиспользованииЭВМ.
19
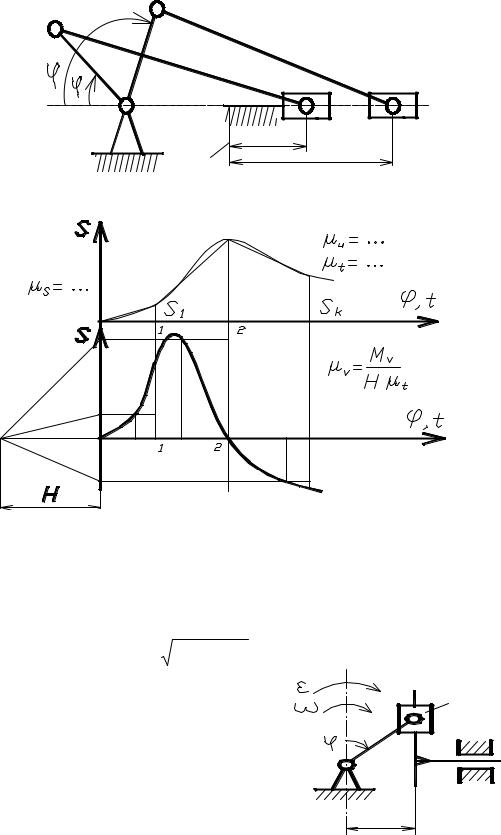
а)
k |
i |
|
|
|
|
|
|
|
|
S |
|
|
|
i |
Sk |
|
крайнее |
|
|
|
|
|
|
|
положение |
|
|
б)
Рис. 19 Рис. 2.6. План положений и кинематическая диаграмма
Рассмотрим пример кинематического исследования синусного механизма (механизмдвойногоползуна), гдекривошип1 вращаетсясугловойскоростью и
угловымускорением |
|
(рис. 2.7). |
Тогда скорость и ускорение точки |
А равны: |
||||||||||
VА = 1ОА· ; |
|
|
|
аА = 1ОА· |
|
( 4 2 ) . |
|
|
|
|||||
|
Все точки звена 1 и 2 описывают |
|
|
2 |
||||||||||
окружности, а точки звена 3 движутся посту- |
|
|
||||||||||||
пательно, имея перемещения, |
скорости и |
|
1 |
A |
||||||||||
ускоренияравные: |
|
|
|
|
|
O |
B |
|
||||||
S В |
1ОА |
sin 1ОА sin t; |
|
|
|
|
||||||||
|
|
|
|
3 |
||||||||||
VВ |
dS В |
/ dt 1ОА cos ; |
|
|
|
|
|
|||||||
|
|
|
|
S |
|
|||||||||
аВ d |
2 |
SВ / dt |
2 |
1ОА ( соs |
|
2 |
sin ); |
|
|
|||||
|
|
|
Рис. 2.7. Синусный механизм |
|||||||||||
при 0 |
аВ= – 1ОА |
|
sin . |
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Р и с . 2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
