
Учебная литература / ulstu2012-116
.pdf
д) |
условие |
правильного |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
зацепления. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Физический |
|
и |
математический |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
смысл этих условий разберем на |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
конкретной |
схеме |
планетарного |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
механизма с нулевыми эвольвент- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ными |
цилиндрическими |
колесами |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(рис. 4.26). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Кинематическое |
|
|
условие |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
обеспечивает заданное передаточное |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
отношение и для данного механизма |
|
|
|
Рис. 4.26. Условия синтеза |
|
||||||||||||||||||||
имеет |
|
|
следующий |
|
|
|
|
вид: |
|
|
|
планетарного механизма: 1 – |
|
||||||||||||
i1,4(H) Z2 |
|
Z4 |
1 |
H , |
|
|
|
|
|
|
|
|
|
солнечное колесо; 2, 3 – блок |
|
||||||||||
|
|
|
|
|
|
|
|
|
сателлитов; 4 – неподвижный |
||||||||||||||||
|
Z1 |
|
Z3 |
4 |
H |
|
|
|
|
|
|
|
|
|
зубчатый венец; Н – водило |
|
|||||||||
или при 4 |
0 |
получим |
|
|
1 |
|
|
|
Z2 |
Z4 . |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
i |
|
1 |
|
|
|
|
|
|
|
(а) |
|||||||||
|
|
|
|
|
|
1,H |
|
|
H |
|
|
|
Z1 |
Z3 |
|
|
|
|
|
|
|
|
|
||
Обычно допускается отклонение передаточного отношения в |
|||||||||||||||||||||||||
пределах 5% от заданного. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Условие соосности требует, чтобы оси колес, 1 и 4 в данном случае, |
|||||||||||||||||||||||||
совпадали для обеспечения зацепления сателлитов с центральными |
|||||||||||||||||||||||||
колесами. Для этого необходимо, чтобы выполнялось соотношение |
|||||||||||||||||||||||||
радиусов |
делительных окружностей |
|
r1 r2 r4 |
|
r3 , а |
при одинаковых |
|||||||||||||||||||
модулях всех колес |
Z1 Z2 Z4 Z3 . |
|
|
|
|
|
|
|
(б) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Условие соседства включает требование совместного размещения |
|||||||||||||||||||||||||
нескольких сателлитов по общей окружности так, чтобы они не задевали |
|||||||||||||||||||||||||
друг друга своими зубьями. Необходимость выполнения этого условия |
|||||||||||||||||||||||||
возникает |
при числе сателлитов |
k 2 |
(увеличение |
числа сателлитов |
|||||||||||||||||||||
уменьшает нагрузку на зубья). В этом случае необходимо, чтобы a |
c |
2 rc |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
( rc – радиус окружности вершин наибольшего сателлита). Так как |
|
|
|||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
) sin ; |
|
|
||
|
|
|
a |
c |
|
2 (r r |
2 |
) |
sin |
m (Z |
1 |
Z |
2 |
|
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
2k |
|
|
|
|
|
|
|
k |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
c |
|
|
|
c |
|
|
|
|
|
|
|
Z |
c |
|
|
|
|
|
|
|
|
|
|
|
|
r |
h a m m |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
ra |
|
|
2 |
1 , |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
то |
|
|
|
sin |
|
|
Zc 2 |
, |
|
|
|
|
|
|
(в) |
||||
|
|
|
|
|
|
|
|
|
k |
Z1 |
Z2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где Zc |
– число зубьев наибольшего сателлита (2 или 3). |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
101 |
|
|
|
|
|
|
|
|
|
|
|
||

Условие сборки учитывает необходимость одновременного зацепления всех сателлитов с центральными колёсами, т. е., установив
первый сателлит и повернув водило на угол 2k рад., необходимо в то же
самое место установить следующий сателлит. Это может быть осуществлено, если зубья колес второго блока сателлитов окажутся точно против впадин зубьев центральных колес. Иначе сборку осуществить невозможно. Для формирования условия примем, что оба колеса всех k блоков сателлитов имеют одинаковую ориентацию зубьев друг относительно друга. После установки первого сателлита на ось водило
должно быть повернуто на угол 2k рад., при этом колесо 1 необходимо повернуть на угол 1 i1,H 2k рад. С другой стороны, угол поворота
колеса 1 ( 1 ) должен быть кратным его угловому шагу зубьев 2 , в Z1
противном случае при повороте на угол 1 положение зубьев колеса 1 изменится и второй сателлит вставить будет невозможно. Таким образом
1 |
q |
2 (q – целое число) |
и |
|
|
|
|
|
||
|
|
Z1 |
2 i1,H |
|
2 |
|
|
|
Z1 |
|
|
|
q |
|
или |
q i1,H |
|
(г) |
|||
|
|
|
Z1 |
|
k |
|
|
|
k |
|
Условие правильного зацепления включает условие отсутствия подреза у колес с внешним зубчатым венцом и условие отсутствия заедания (интерференции) во внутреннем зацеплении. Эти условия имеют вид:
Zi Zmini .
Значение Zmin можно принять равным:
Zmin 17 – для колес с внешним зацеплением;
20 |
– для колес с внутренним зацеплением. |
(д) |
|
Zmin |
|
||
85 |
|
|
|
4.15.2. Методы синтеза эпициклических механизмов
Задача подбора чисел зубьев колес для эпициклического механизма в общей постановке является оптимизационной ввиду множества возможных решений. Ее можно считать типичной задачей дискретного нелинейного программирования, если за критерий оптимальности принять габариты или вес механизма, а ограничениями на целочисленные
102

параметры Z1, Z2,… будут условия (а-д). Такую задачу можно решать различными методами, например, численными методами направленного перебора, когда варьируются Z1, Z2,… с целью минимизации габаритов или веса при соблюдении ограничений. Такая задача может быть решена с помощью ЭВМ.
Применяются упрощенные методы, позволяющие найти одно из конструктивно допустимых решений. Один из таких методов – метод
сомножителей. |
|
|
|
|
|
|
|
|
|
Представим числа зубьев в виде нескольких сомножителей: |
|
||||||||
|
Z1 A t ; |
Z2 B t ; |
Z3 C t ; |
Z4 D t . |
|
||||
Из условия (б) (A B) (D C) . Это уравнение превращается |
|||||||||
в тождество при: D C ; |
A B . |
|
|
|
|
||||
Тогда: |
Z1 t A (D C) ; |
Z2 t B (D C) ; |
|
|
|
|
|||
|
Z3 t C (A B) ; |
Z4 t D (A B). |
|
B |
D i1,H |
|
|||
Подставив эти выражения в условие (а), получим: |
|
1. |
|||||||
|
A |
||||||||
|
|
|
|
|
|
|
C |
|
|
Таким |
образом, |
величину |
(i1,H |
1) можно представить в |
виде |
||||
нескольких сомножителей (A, B, C, D). Далее определяются значения t, обеспечивающие выполнение условий сборки и правильного зацепления, и выбирается одно из этих значений. Например, из условия сборки (г)
A (D C) i1,H
k
выбираются значения t, обеспечивающие целочисленность q. После этого можно определить числа зубьев.
Пример: |
|
i1,H 15 ; |
k 3. |
|
|
|
|
|
|
|||||
Представим |
|
B |
|
D |
i1,H 1 15 |
1 14 |
2 7 |
, т. е. А=1; В=2; С=1; |
||||||
|
|
C |
1 1 |
|||||||||||
D=7. Тогда |
|
|
A |
|
|
|
|
|
|
|
|
|||
|
|
|
|
A |
(D C) i1,H |
|
|
1 (7 1) 15 |
|
|
||||
|
q t |
t |
30 t , |
|
||||||||||
|
|
|
k |
|
3 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
следовательно, |
условие сборки выполняется при t 1, 2,... |
Так как при |
||||||||||||
t 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1 1 1 (7 1) 6 ; |
|
|
Z2 1 2 (7 1) 12 ; |
|
Z3 1 1 (1 2) 3 ; |
|||||||||
Z4 1 7 (1 2) 21, то с учетом условий правильного зацепления, когда |
||||||||||||||
Zmin3 20 , принимаем |
t 7 . Тогда |
Z1 42 ; |
Z2 84 ; |
Z3 21; |
||||||||||
Z4 147 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
103
4.16. Эпициклические механизмы с коническими колесами
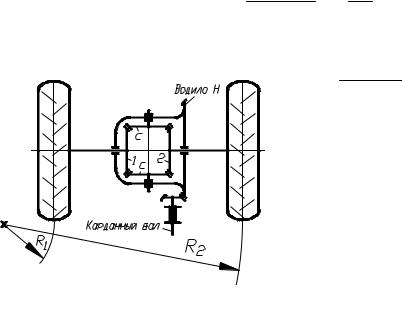
Примером дифференциального механизма с коническими колесами является дифференциал автомобиля (рис. 4.27). Согласно формуле Виллиса
1 |
H Z2 . |
|
|
|
|
|
2 |
H |
Z1 |
|
Z1 |
|
|
|
При |
Z2 |
получим |
|||
|
Н |
1 2 |
, т. |
е. |
при постоянной |
|
|
|
2 |
|
|
|
|
|
скорости вращения карданного вала и |
|||||
|
скорости автомобиля в целом полуоси |
|||||
|
могут |
вращаться |
с |
различными или с |
||
|
одинаковыми скоростями. Например, на |
|||||
|
повороте скорости вращения полуосей |
|||||
|
пропорциональны |
радиусам |
поворота |
|||
|
R1 и R2, а при ровной прямой дороге |
|||||
|
скорость полуосей одинакова и равна |
|||||
Рис. 4.27. Автомобильныйдифференциал |
|
1 2 |
Н . |
|
||
Рис. 1.22 |
|
|
|
|
|
|
Контрольные вопросы
1.Какие механизмы называют фрикционными?
2.Какие механизмы называют зубчатыми?
3.По каким признакам классифицируются зубчатые механизмы?
4.Какие зубчатые механизмы называются плоскими?
5.Какие зубчатые механизмы называются пространственными?
6.Какие зубчатые механизмы называются редукторами?
7.Какие зубчатые механизмы называются мультипликаторами?
8.Какие зубчатые механизмы называются эпициклическими?
9.Какие звенья называются сателлитами?
10.Какие звенья называются водилами?
11.Какие колеса называются центральными, солнечными?
12.Какие зубчатые механизмы называются планетарными редукторами?
13.В чем заключается условие соосности для планетарных редукторов?
14.Назовите преимущества и недостатки планетарных редукторов.
15.Где и в каких целях применяются планетарные редукторы?
16.Что такое обращенный механизм?
104
17.Что такое передаточное отношение планетарного редуктора?
18.Каким образом определяются передаточные отношения планетарных редукторов?
19.Как строится картина скоростей?
20.Как строится план угловых скоростей?
21.Как определяется передаточное отношение планетарного редуктора графическим построением?
22.Классификация зубчатых колес.
23.Классификация зубчатых передач.
24.Эвольвента и ее основные свойства.
25.Способы нарезания зубчатых колес.
26.Основные параметры зубчатых колес: основная, делительная и начальная окружности, окружности выступов, впадин, модуль зацепления, шаг, дуга, линия зацепления.
27.Подрезание профиля зуба. Корригирование зубчатого колеса.
105

5. МАШИНЫ-АВТОМАТЫ И ИХ СИСТЕМЫ УПРАВЛЕНИЯ
5.1. Основные понятия теории машин-автоматов
Кроме машин, в которых человек-оператор осуществляет управление практически всеми операциями, существуют устройства полуавтоматического и автоматического действия.
Полуавтомат – это машина с автоматическим циклом работы, для повторения которого необходимо участие человека, выполняющего лишь некоторые операции, например, по включению для повторений цикла, загрузке, выгрузке и т. д.
Машина-автомат (МА) – машина с автоматической системой управления, где все операции выполняются без участия человека, а его функции включают лишь наблюдение, наладку при изготовлении новых деталей, контроль и ремонт.
Автоматическая линия (АЛ) – это совокупность (МА), соединенных автоматическими транспортными устройствами с общей системой управления.
Указанные машины характеризуются производительностью Q – это число единиц продукции, выпускаемой в единицу времени t: Q N / t (N –
общее число единиц).
Различают технологическую (идеальную) Qи , цикловую Qц и фактическую Qф производительность.
Qи 1/ t р |
( t р – время, |
затраченное на единицу продукции без |
простоев). |
|
|
Qц Nц / Tk |
Nц /(t x t p ) , |
Nц – число единиц продукции, |
выпускаемой за время кинематического цикла Tk , включающего время холостого t x и рабочего t p хода.
Qф Nц н Qц н , где н – коэффициент использования
Tk
машины.
В машине-автомате выделяют следующие основные узлы (рис. 1): Двигатель (мотор) (М); передаточный механизм (ПМ); рабочая
машина (РМ); система автоматического управления (САУ). Передаточный механизм преобразует (передает) движение от М к РМ,
которая обеспечивает выполнение требуемых операций |
с обрабатывае- |
|||
мым предметом. |
|
|
|
|
САУ – |
это |
совокупность |
устройств, |
обеспечивающих |
согласованность перемещений и действий всех рабочих органов. |
||||
Работа |
МА |
характеризуется |
рабочим, кинематическим и |
|
|
|
106 |
|
|
технологическим циклами ( Тр,Тк,Тт ). За Тр машина выдает |
очередное |
||
изделие. |
Тт – время нахождения изделия в обработке. |
Тк – время |
|
установки рабочих органов в исходное положение. |
|
|
|
(МА) и (АЛ) классифицируются: |
|
const и |
|
1) по |
характеру Тк на специализированные с |
Тк |
|
универсальные с Тк var ;
2)по характеру перемещения обрабатываемого изделия: с непрерывным, периодическим и смешанным перемещением;
3)в зависимости от числа позиций при обработке на одно и многопозиционные МА;
4)по принципу действия выделяют МА и АЛ последовательного, параллельного и смешанного действия.
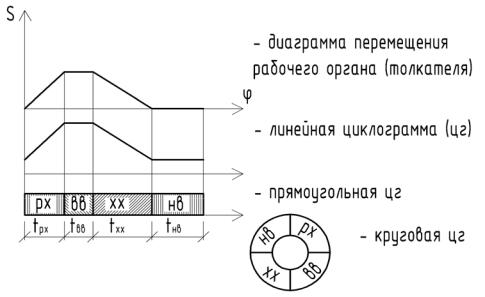
Графически последовательность работы МА или его механизмов можно представить в виде циклограммы (рис. 5.1).
Рис. 5.1. Пример циклограмм
ЦГ машины – это схема согласованности перемещений рабочих органов в зависимости от времени или угла поворота главного вала машины. Она показывает последовательность работы каждого механизма и на ней ЦГ всех механизмов совмещены.
Для точного расчета циклограммы иногда строят так называемую синхрограмму, т. е. совокупность диаграмм перемещений отдельных рабочих органов, построенных в единой системе координат. За начало построения принимается одно из крайних положений основного исполнительного механизма (начало рабочего хода).
107
5.2. Системы управления машин-автоматов
Системы управления СУ обеспечивают управление работой МА в заданном режиме и функциональной взаимосвязи механизмов по определенной программе.
Программа – это совокупность команд, обеспечивающих выполнение техпроцесса.
СУ обычно включает: 1 – программоноситель; 2 – считывающее устройство; 3 – передаточное устройство; 4 – управляющий орган. Иногда в СУ входят узел обратной связи и самонастройки, воспринимающие текущую информацию о результатах работы с последующей коррекцией рабочих параметров.
По виду программоносителя СУ делятся на СУ с распределительным валом, с копирами, с упорами, числовым программным управлением.
СУ с распределительным валом включают распредвал (РВ), т. е.
вращающееся звено, являющееся ведущим для всех исполнительных механизмов. На РВ закреплены детали (рычаги, кривошипы, кулачки) управляющие рабочими органами. Требуемая последовательность работы рабочих органов обеспечивается при этом закреплением кулачков, рычагов на РВ под определенными углами. Для уменьшения нагрузки на РВ применяют СУ (рис. 5.2, а) с командоаппаратом (КА), представляющим устройство с двигателем 1, вращающим вал 2 с кулачками, которые управляют работой электровыключателей 3. Сигналы от электровыключателей воздействуют на силовые системы привода рабочих органов. Вместо электровыключателей могут стоять золотники и распределители в системах с гидро- и пневмоприводом.
СУ с копирами включают копир (рис. 5.2, б) 1 – копию (образец) детали, являющийся программоносителем. Щуп 2 является считывающим устройством, а штанга 3 – передаточным устройством, управляющим рабочим органом 3 (режущим инструментом).
Рис. 5.2. Системы управления: а – с командоаппаратом; б – с копиром
108
СУ с упорами. Упоры – это детали с выступами, установленные по линии движения МА и воздействующие на путевые переключатели или конечные выключатели, которые включают – выключают приводы рабочих органов. Такие СУ еще называются СУ по пути (путевые).
Системы числового программного управления СЧПУ) имеют специальный регулируемый привод рабочих органов с шаговым двигателем. Информация о перемещенияx s рабочего органа выражается
дискретными числами s n s , где |
s – шаг, т. е. цена одного сигнала, |
мм. Эта информация кодируется |
на простых программоносителях |
(магнитные ленты и т. д.). В СЧПУ с обратной связью имеется дополнительный блок обратной связи, в котором производится сравнение фактического s и заданного s параметра, например, перемещения, в результате чего вырабатывается сигнал рассогласования s s s , по
которому корректируется параметр движения с подачей сигнала на двигатель рабочего органа.
Контрольные вопросы
1.Что такое машина-автомат?
2.Какова структура машин-автоматов?
3.Что такое система управления машин-автоматов?
4.Что называется циклограммой?
5.Виды циклограмм.
6.Что такое синхрограмма?
6.ОСНОВЫ СТРУКТУРЫ И КИНЕМАТИКИ МАНИПУЛЯТОРОВ
ИПРОМЫШЛЕННЫХ РОБОТОВ
6.1.Виды манипуляторов и промышленных роботов
Вкачестве средств механизации применяются манипуляторы и промышленные роботы.
Манипулятором называется техническое устройство, предназначенное для воспроизведения рабочих функций руки человека. Первые конструкции и по внешнему виду напоминали руку человека. На рис. 6.1 показана схема копирующего манипулятора, состоящего из управляющего (У) и исполнительного (И) механизмов. Вследствие идентичности, движения звеньев исполнительного механизма копируют движения управляющего благодаря электромеханической связи между ними.
109
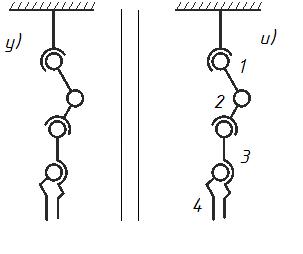
Рис. 6.1. Схема копирующего манипулятора
Механизм манипулятора представляет собой пространственную кинематическую цепь, звенья которой по аналогии с рукой называются О – корпус; 1 – плечо; 2 – предплечье; 3 – кисть (захват); 4 – палец. Плечо с корпусом образуют кинематическую пару, называемую плечевым суставом; аналогично: 1-2 – локтевой сустав; 2-3 – кистевой сустав. Звено 4 (палец) при рассмотрении структуры, кинематики и динамики
манипулятора |
объединяются со звеном 3. Т. е. степень подвижности |
|
манипулятора |
W 6n 5 р5 4 р4 ...Р1 6 3 5 1 3 2 7 |
(число |
степеней свободы незамкнутой кинематической цепи равно сумме подвижностей кинематических пар.
Копирующие манипуляторы используются в местах, исключающих присутствие человека. В зависимости от системы управления различают манипуляторы с ручным и автоматическим управлением.
В манипуляторах с автоматическим управлением звенья получают движение от приводов, работающих по заданной программе. Предварительно на программу записываются действия оператора, связанные с перемещением звеньев управляющего механизма (на перфоленту или магнитные носители). После этого программа может многократно использоваться.
Промышленные роботы (ПР) – это манипуляторы с автоматическим управлением, отличающиеся от обычных машинавтоматов применением механизмов, образованных из незамкнутых кинематических цепей, возможностью быстрой переналадки на выполнение различных программ, широким диапазоном пространственных движений рабочих органов.
Манипуляторы с автоматическим управлением, применяемые в машинах-автоматах для выполнения различных транспортных операций (загрузка, перемещение, выгрузка изделий и т. д.), работающие по жесткой (неизменяемой) программе называются автооператорами.
Конструктивные схемы манипуляторов ПР разнообразны, например
110
