Учебная литература / n1

На промежутке от 0 до π2 действует только момент движущих

сил M Д . Следовательно, избыточная работа, кинетическая энергия и угловая скорость будут возрастать.

На промежутке от π2 до π момент сил сопротивления MC

больше момента движущих сил. Следовательно, избыточная работа будет отрицательной (она изображается площадью прямоугольника NFKP ) и кинетическая энергия и угловая скорость будут убывать.

Затем по аналогичным причинам угловая скорость будет возрас-

уравнение движения и для перемещения от ϕ = π2 до ϕ =π ).

483

Коэффициент неравномерности хода

δ = ωmax −ωmin = 10,3 −9,35 = 0,096 ωср 9,82

Чтобы найти угловое ускорение звена приведения, воспользуемся уравнением движения в дифференциальной форме

5.8Контрольные вопросы

1.Классифицируйте силы, действующие в машине.

2.Что называют механической характеристикой?

3.Как подсчитать кинетическую энергию звена при его поступательном, вращательном, плоском движении? Чему равна кинетическая энергия машины?

4.Какие различают этапы (режимы) работы машины?

5.Сформулируйте закон передачи работы при установившемся движении.

484

6.Покажите возможные динамические модели машинного агрегата с жесткими звеньями с одной степенью подвижности.

7.Что является критерием приведения сил и масс в машине?

8.Что называют приведенной массой, приведенным моментом инерции? Приведите пример по определению Iпр. (mпр.).

9.Что называют приведенной силой, приведенным моментом? Приведите пример по определению Рпр. (Мпр.).

10.Сформулируйте теорему Н.Е. Жуковского о жестком рычаге. Как определить Рпр., Мпр. с помощью рычага Жуковского?

11.Запишите уравнение движения машины в энергетической (интегральной) форме. Как найти с помощью этого уравнения закон движения машины?

12.Запишите уравнение движения машины в дифференциальной форме (уравнение Лагранжа 2-го рода). Как найти закон движения машины с помощью этого уравнения?

13.Что называют диаграммой энергомасс? Как определяют закон движения звена приведения с помощью этой диаграммы?

14.Отчего возникают колебания скорости главного вала машины при установившемся движении? Что называют коэффициентом неравномерности хода машины?

15.Расскажите, в какой последовательности решают задачу динамического анализа машинного агрегата с помощью диаграммы энергомасс.

6 Комплексная контрольная работа (итоговый тест)

Контрольная работа выполняется в присутствии преподавателя. Студент должен ответить в письменной форме на вопросы, изложенные в пункте 6.1., применительно к одному из машинных аг-

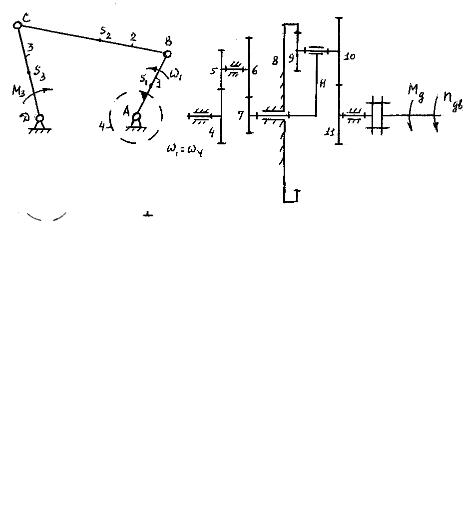
регатов, показанных на рисунках 5.35 – 5.39.

6.1 Содержание контрольной работы

Для машинного агрегата, указанного в задании:

1.Определить степень подвижности планетарной ступени зубчатого механизма (8).

2.Провести структурный анализ рычажного механизма (7).

485

3.Зная числа зубьев колес зубчатого механизма и частоту враще-

ния nдв. ротора электродвигателя (или nраб. – рабочей машины), найти частоту вращения кривошипа АВ (10).

4.Построив планы скоростей и ускорений рычажного механизма, определить величины и направления угловых скоростей и ускорений звеньев. Определить характер движения звеньев (ускоренное или замедленное) (20).

5.Определить динамические нагрузки, действующие на подвижные звенья рычажного механизма, записав формулы для подсче-

та главного вектора Фi и главного момента Мфi сил инерции и приложив их к каждому звену (15).

6.Считая известными массы и моменты инерции всех подвижных

звеньев, положения их центров масс, значения силы Р3 или момента М3 и момента Мдв (или Мс), построить динамическую модель машинного агрегата, принять за звено приведения кривошип 1, и составить выражения для подсчета приведенного момента Мпр1 и приведенного момента инерции Iпр1 (20).

7.Для полученной динамической модели записать уравнения движения в энергетической и дифференциальной формах. Изложите, как с помощью этих уравнений определяют закон движения звена приведения (20).

Вскобках указано максимальное количество баллов, которое можно получить при ответе на вопрос.

Чтобы определить оценку, полученную за выполнение задания, необходимо суммарное количество баллов разделить на 20.

486

6.2. Задания к комплексной контрольной работе.

Задание1

Рисунок 5.35

Задание 2

Рисунок 5.36

487

Задание 3

Рисунок 5.37

Задание 4

ϕ1

Рисунок 5.38

488

Задание 5

Рисунок 5.39

489