r |
r |
r |
|
V |
= V |
+ V . |
|
C |
B |
CB r |
известно: параллельно направляющей. |
Направление VC |
Из плана скоростей видно, что
VC = VB = 9 м/с.
Чтобы найти реакцию R03n , необходимо рассчитать структурную
группу 2 – 3 (рисунок 4.32с).
Так как массы звеньев не заданы, то расчет ведем без учета динамических нагрузок, т.е. сил инерции.
Тогда на структурную группу будут действовать следующие си-
лы:
заданная сила Р3, реакция в поступательной паре R03 = R03n + F ,
реакция во вращательной паре R12 |
= R12n + R12τ (рисунок 4.32с). |
|
запишем уравнение равновесия группы в виде |
|
|
∑mB |
(Pi )= R03n h1 − F h2 − P3 h2 = 0 |
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R n l |
BC |
cos α − f R n l |
BC |
sin α − P l |
BC |
sin α = 0 . |
|
03 |
|
|
|
|
|
03 |
|
3 |
|
|
|
|
|
Из рисунка 4.32а видно, что |
|
|
|
|
|
|
|
sin α = |
lAB |
= |
0,1 |
= 0,25. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lBC |
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда α = 14,47°. |
|
|
|
|
|
|
|
|
|
|
Rn = |
|
|
|
|
P l |
BC |
sin14,47o |
|
|
= |
|
1000 |
0,4 0,25 |
= |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
lBC cos14,47o |
− f lBC sin14,47o |
|
|
|
03 |
|
0,4 |
0,968 |
−0,1 0,4 0,25 |
|
= 265,1 H. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N = f R n |
V = 0,1 265,1 9 = 238,59 Вт. |
|
|
|
|
|
|
|
03 |
C |
|
|
|
|
|
|
|
|
|
|
|
|
Задача 5
Для кулисного механизма (рисунок 4.33а) найти уравновешивающий момент Му, приложенный к звену АВ, если к кулисе 3 при-
ложен момент М3 = 4 Нм, углы ϕ1 = 90°, ϕ3 = 30°, длина lАВ = 0,1 м.
Решение
Определим Му с помощью рычага Жуковского.
Строим план скоростей (рисунок 4.33b), используя уравнения
VB1, 2 = ω1 lAB ,
VB3 = VB1,2 + VB3B1,2
VB3 = VC + VB3C .
Рисунок 4.33 Для построения рычага Жуковского представим момент М3 в
виде пары сил с силами P |
= P |
|
= |
M3 |
, перпендикулярными к пле- |
|
|
|
|
|
|
|
|
B |
3 |
C |
|
lBC |
|
|
|
|
|
|
|
|
|
|
|
|
|
чу ВС. |
|
|
|
|
|
|
0,1 |
|
|
|
|
|
Так как lBC = |
lAB |
= |
|
|
= 0,2 м. |
sin ϕ3 |
sin 30 |
|
|
|
|
|
|
|
|
|
|
|
P |
= P = |
4 |
|
= 20 H. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
C |
0,2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Будем также считать, что к точке В перпендикулярно к кривошипу приложена уравновешивающая сила Ру.
Перенесем эти силы в соответствующие точки плана скоростей, предварительно повернув их на 90° против хода часовой стрелки
(рисунок 4.33b).
Записываем уравнение равновесия рычага
Pу |
pb |
1,2 − PB3 |
|
pb |
3 |
= 0 , |
|
|
P |
= P |
|
|
pb |
3 |
|
= P |
sinϕ |
|
= 20 sin30 =10 H . |
|
|
|
|
|
|
у |
|
|
B3 |
|
pb1,2 |
|
|
|
B3 |
3 |
|
Тогда
Му = Ру lАВ = 10 0,1 = 1 Нм.
4.10 Силовой анализ рычажного механизма аналитическим способом
Аналитический метод силового расчета, тем более с использованием ЭВМ, требует введения определенных правил при выборе систем координат, способе описания приложенных сил, записи уравнений равновесия, одинаково трактуемых как расчетчиком, так и ЭВМ.
Система координат
Система координат выбирается так же как и при кинематическом анализе механизмов: используем правую прямоугольную систему координат с началом на оси вращения входного звена.
При наличии в механизме неподвижной направляющей направляем ось абсцисс параллельно этой направляющей.
Если в механизме несколько непараллельных неподвижных направляющих, то кроме основной системы координат с осью абсцисс, направленной параллельно неподвижной направляющей, принадлежащей структурной группе, наиболее удаленной в соответствии с формулой строения механизма от начального механизма, вводят дополнительные системы координат.
Силовой расчет структурных групп в этом случае выполняют, используя для каждой из них свою систему координат, а при переходе от группы к группе применяют для определения реакций в кинематических парах формулы преобразования.
Рисунок 4.34
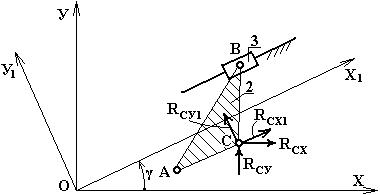
Пусть требуется рассчитать структурную группу 2-3 в системе координат Х1 ОУ1, зная реакцию в шарнире С, найденную из расчета предыдущей группы в системе координат ХОУ и представленную
проекциями Rcx и Rcy.
Чтобы перейти от этих проекций к проекциям Rcx1 и Rcy1 , используют стандартные формулы преобразования
|
RCX 1 |
= RCX cosγ + RCY sin γ |
(4.63) |
|
RCY1 |
= −RCX sin γ + RCY cosγ |
|
|
Здесь γ - угол между осью Х основной системы координат и осью Х1
дополнительной системы , отсчитываемый от оси Х против часовой стрелки.
Для возврата в основную систему координат также используют стандартные формулы
|
RCX |
= RCX 1 cosγ − RCY1 sin γ |
(4.64) |
|
RCY |
= RCX 1 sin γ + RCY1 cosγ |
|
|
Описание сил
Для описания силы необходимо указать модуль силы, координаты точки ее приложения, угол α между силой и основным вектором звена, отсчитываемый от основного вектора против хода часовой стрелки и угол φ, определяющий направление основного вектора звена (рисунок 4.35).
Рисунок 4.35 щим формулам
FX = F cos(ϕ +α) FY = F sin(ϕ +α)
Так как в уравнениях равновесия будут участвовать проекции сил на координатные оси, то полезно предварительно подсчитать величины этих проекций.
Проекции силы F , изоб-
раженной на рисунке 4.35, будут определяться по следую-
(4.65)

Силы инерции звеньев представляют в виде главного вектора Ф и главного момента МФ сил инерции .
На расчетной схеме показывают обычно проекции ФХ и ФУ главного вектора сил инерции .
Причем эти проекции направляют в положительном направлении соответствующей оси (рисунок 4.36) и подсчитывают по формулам
|
|
&& |
|
|
ФХ = −mX S |
(4.66) |
|
Ф = −mY&& |
|
|
|
У |
S |
|
Здесь
X&&S , Y&&S - проекции ускорения центра масс звена на координатные оси.
Истинные направления этих проекций определятся знаками X&&S
и Y&&S .
Главный момент МФ сил инерции показывают на расчетной схеме (рисунок 4.36) также направленным в положительном направлении, т.е. против хода часовой стрелки, и определяют по формуле
где
IS - момент инерции звена относительно оси, проходящей через центр масс звена перпендикулярно к плоскости движения звена; ϕ&& - угловое ускорение звена.
Момент силы относительно точки
Момент любой силы, представленной в виде проекции на координатные оси, относительно некоторой точки подсчитывают по следующей стандартной формуле
mA (F) = FY(XK - XA) – FX(YK –YA) |
(4.68) |
Здесь
XK , YK – координаты точки приложения силы F;
XA, YA – координаты точки, относительно которой определяют моменты силы.
Реакции в кинематических парах
Реакцию во вращательной паре показывают ее проекциями на координатные оси, направленными в стороны положительных направлений осей (рисунок 4.37).
Реакцию в поступательной паре направляют перпендикулярно к неподвижной направляющей в сторону положительного направления соответствующей оси и смещая в общем случае на некоторое расстояние h относительно шарнирной точки ползуна (рисунок
4.38).
Реакцию кулисного камня на кулису представляют ее проекциями. Направление полной реакции определяют путем поворота ос-
новного вектора lB3C кулисы на 90º против хода часовой стрелки
(рисунок 4.39).
Тогда проекции этой реакции на координатные оси определяется по формулам (рисунок 4.39)
R23X = R23 cos(φ3 + 90) |
|
R23Y = R23 sin(φ3 + 90) |
(4.69) |
Здесь |
|
φ3 – угол, определяющий направление основного вектора lB3C
кулисы. Этот угол находят в ходе кинематического анализа механизма.
Реакцию в высшей кинематической паре (рисунок 4.40) также представляют двумя ее проекциями.
R12X = R12 cos α |
|
R12Y = R12 sin α |
(4.70) |
При известном угле α , определяющим направление нормали n-n к соприкасающимся профилям, в выражениях (4.70) присутствует только один неизвестный параметр – величина реакции R12.
Пример силового анализа шестизвенного механизма
Провести силовой анализ шестизвенного механизма, показанного на рисунке 4.41.

Дано: |
Рисунок 4.41 |
|
|
lАВ = 0,14м, lСД = 0,77м, lДЕ = 0,28м, |
lCS3 = 0,385м, |
lДS4 = 0,14м, |
хС = 0, уС = -0,4м, уЕ = 0,3м, |
уН = 0,225м, ω1 = 20 с-1. |
Массы звеньев: m1 = 10 кг, m2 = 15 кг, |
m4 = 4 кг, |
m5 = 30 кг. |
Моменты инерции звеньев относительно центральных осей, перпендикулярных плоскости движения: IS3 = 1,1 кг м2, IS4 = 0,04 кг м2.
Сила технологического (полезного ) сопротивления: РС =2100 Н. Кривошип вращается по часовой стрелке и приводится во вра-
щение через зубчатую передачу «а - в».
Радиус основной окружности колеса «в» - rв = 0,2м , угол зацепления в паре колес αw = 26º.
Требуется определить: реакции в кинематических парах, уравновешивающую силу, приложенную в полюсе П (усилие в зацепле-
нии), при φ1 = 45º.
Решение: Для силового анализа механизма предварительно проводят его кинематический анализ в заданном положении с целью определения ускорений центров масс и угловых ускорений звеньев.
Результаты этого анализа представлены в таблице 4.1. В ней обозначено:
х, у – координаты точки; х′, у′ - проекции аналога скорости точки;
х′′, у′′ - проекции аналога ускорения точки; &x&, &у& - проекции ускорения точки;
φ, φ′, φ′′, ϕ&& - соответственно угол поворота, аналог угловой
скорости, аналог углового ускорения и угловое ускорение звена. При использовании ЭВМ для силового анализа механизмов ки-
нематический анализ реализуется в виде отдельной подпрограммы. Таблица 4.1
|
|
|
|
|
|
|
|
|
|
|
&& |
|
|
|
&& |
Точка |
х, м |
|
у, м |
|
х′, м |
|
у′, м |
х′′, м |
|
у′′, м |
x, |
|
|
|
у , |
|
|
|
|
м/с2 |
|
|
|
м/с2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Структурная группа (2,3) |
|
|
|
|
|
|
В1,2 |
0,09899 |
|
0,09899 |
|
-0,09899 |
|
0,09899 |
-0,09899 |
|
-0,09899 |
-39,598 |
|
|
|
-39,598 |
В3 |
0,09899 |
|
0,09899 |
|
-0,114 |
|
0,0226 |
-0,0466 |
|
-0,1789 |
-18,54 |
|
|
|
-71,568 |
S3 |
0,07492 |
|
-0,02236 |
|
-0,0864 |
|
0,0171 |
-0,03827 |
|
-0,0135 |
-14,107 |
|
|
|
-5,416 |
|
|
|
|
|
Структурная группа (4,5) |
|
|
|
|
|
|
Д |
0,1498 |
|
0,3553 |
|
-0,1727 |
|
0,0343 |
-0,0705 |
|
-0,027 |
-28,214 |
|
|
|
-10,832 |
Е,S5 |
0,4243 |
|
0,3 |
|
-0,1797 |
|
0 |
-0,0695 |
|
0 |
-27,814 |
|
|
|
0 |
S4 |
0,2871 |
|
0,3276 |
|
-0,1762 |
|
0,0171 |
-0,07 |
|
-0,0135 |
-28,014 |
|
|
|
-5,416 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Звено |
φ,градус |
|
|
φ′ |
φ′′ |
&& |
, с |
-2 |
|
|
ϕ |
|
2 |
258,8 |
|
0,228 |
0,083 |
|
33,2 |
|
3 |
258,8 |
|
0,228 |
0,083 |
|
33,2 |
|
4 |
248,6 |
|
-0,125 |
0,0955 |
|
38,2 |
|
5 |
|
0 |
|
|
0 |
0 |
|
|
|
0 |
|
При кинематическом и силовом анализе механизма используется правая прямоугольная система координат, показанная на рисунке
4.41а.
Последовательность силового расчета
Из структурной схемы (рисунок 4.41б) и формулы строения видно, что в первую очередь необходимо рассчитать группу (4,5), затем
– группу (2,3) и кривошип 1.
Определение сил тяжести и сил инерции звеньев
Так как масса звена 2 не задана, то силой тяжести и силами инерции этого звена пренебрегаем.
При подсчете величин сил тяжести звеньев примем g ≈10 м/с2.
G1 |
= m1 ·g = 10 |
· 10 = 100 Н, |
G3 = m3 ·g = 15 · 10 = 150 Н, |
G4 |
= m4 ·g = 4 · |
10 = 40 Н, |
G5 = m5 ·g = 30 · 10 = 300 Н. |
Ф1Х = Ф1У = 0, МФ1 = 0, т.к. аS1 = 0 и ε1 = 0.
Ф3Х = -m3 ·&x&S 3 = - 15 · (-14,107) = 211,6 Н Ф3У = -m3 · &y&S 3 = -15 · (-5,416) = 81,24 Н МФ3 = -IS3 ·&y&S 3 = -1,1 · 33,2 = -36,524 Нм Ф4Х = -m4 · &x&S 4 = - 4· (-28,014) = 112,06 Н Ф4У = -m4 · &y&S 4 = - 4 · (-5,416) = 21,66 Н МФ4 = -IS4 ·&y&4 = - 0.04 · 38,2 = -1,528 Нм Ф5Х = -m5 · &x&S 5 = - 30 · (-27,814) = 834,42 Н
МФ5 = 0, т.к. ε5 = 0.
Расчет структурной группы (4,5)
Расчетная схема показана на рисунке 4.42 Уравнение равновесия:
- для группы (4,5)
∑Fix = R34x + Ф4х + Ф5х – Рс =0
Отсюда
R34 x = РС −Ф4x −Ф5х = 2100 −112,06 −834,42 =1153,52Н
∑ Fiу = R34у + Ф4у – G4 – G5 + R05 = 0
Неизвестные величины отмечены чертой.









