Учебная литература / n1

Отсюда

n4 = −n5 (4) .

1 U58

Тогда

U15 =1+ U14H (1/(1− U58(4) )−1).

3.4.5 Кинематика волновых передач

Как частный случай сателлитной передачи, рассматривают волновую передачу, которая может быть как зубчатой, так и фрикционной.

Особенностью волновой передачи является то, что одно из зубчатых колес планетарной передачи с внутренним зацеплением является гибким, непрерывно деформирующимся во время работы (ри-

сунок 3.28).

Конструктивно гибкое колесо 2 выполнено в виде тонкостенного стакана с упруго деформируемым зубчатым венцом.

Деформация колеса осуществляется с помощью генератора волн Н, который вставляется внутрь колеса 2.

Рисунок 3.28

333

Генератор волн, выполненный либо в виде водила с роликами, либо в виде кулачка симметричной формы, деформирует гибкое колесо и вводит его в зацепление с жестким колесом.

В зависимости от количества роликов на генераторе может быть несколько зон зацепления.

Передача с двумя зонами зацепления называется двухволновой (рисунок 3.28а), с тремя зонами зацепления – трехволновой (рису-

нок 3.28б).

Обычно разность чисел зубьев Z3 – Z2 невелика и кратна числу волн.

По замыслу изобретателя этой передачи (Массер, США) Z3 – Z2

= 2.

При вращении генератора Н в каждой зоне зацепления возникает бегущая волна деформации и за счет этого происходит обкатывание одного колеса относительно другого.

Если неподвижно жесткое колесо 3, то вращается гибкое колесо 2 в сторону, противоположную направлению вращения генератора Н.

Если неподвижно гибкое колесо 2, то вращается жесткое колесо 3 в ту же сторону, что и генератор.

Достоинствами волновой передачи являются возможность получения больших передаточных отношений, передачи больших нагрузок при сравнительно малых размерах (результат многопарного зацепления зубьев), достаточно высокий коэффициент полезного действия (при передаточных отношениях 100…400 КПД достигает 0,8 – 0,9).

С помощью волновой передачи можно передать вращение через герметичную стенку, что имеет существенное значение при реализации технологических процессов в средах, опасных для жизни человека.

Пример возможного решения этой задачи показан на рисунке 3.29, где пространства А и Б разделены герметично посредством стенки стакана 2 с одновременной передачей вращения от звена 1 к звену 3.

334

Рисунок 3.29 Недостатком волновой передачи является наличие гибкого зуб-

чатого колеса, многократная деформация которого может вызвать его усталостное разрушение.

Передаточное отношение волновой передачи можно определить, если воспользоваться методом обращения движения (методом остановки генератора Н).

Если волновой передаче сообщить вращение с угловой скоростью “−ωH”, то получим рядовую передачу, состоящую из пары ко-

3.5 Графический метод определения передаточных отношений

Изучив этот параграф, студент должен уметь:

-строить картину распределения скоростей точек зубчатых колес и диаграмму угловых скоростей звеньев;

335

-определять скорость любой точки, угловую скорость любого звена зубчатой передачи;

-определять величину и знак передаточного отношения.

3.5.1. Построение картины распределения скоростей звеньев и диаграммы угловых скоростей

Графический метод базируется на построении картины распределения скоростей точек зубчатых колес.

Так как при вращательном движении звена скорости его точек прямо пропорциональны их расстояниям до абсолютной оси враще-

ния, то для построения линии распределения скоростей

звена необходимо знать значения скоростей двух любых его точек.

Построим картину распределения скоростей для рядовой зубчатой передачи, состоящей из двух колес.

Для этого вычерчиваем в масштабе кинематическую схему этого механизма, показывая на ней начальные окружности зубчатых колес (рисунок 3.20а).

Для колес без смещения (нулевых колес) радиусы начальных ок-

Покажем скорость точки “П” (рисунок 3.30а), отложив перпендикулярно к радиусам О1П и О2П (а следовательно, и к линии центров О1О2) произвольный отрезок Пп.

Тогда на колесе 1 будут известны скорости двух точек - “П” и “О1” (она равна нулю). Проведя через точки “п” и “О1” прямую, получим линию 1 распределения скоростей колеса 1.

336

Аналогично строится линия 2 (О2п) распределения скоростей колеса 2. Полученная картина называется картиной распределе-

Картина распределения скоростей позволяет найти скорость любой точки колеса. Так, чтобы найти скорость точки “K” колеса 2, необходимо радиусом из центра О2 (рисунок 3.30а) перенести точку “K” на линию центров, провести параллельно

Пп отрезок К1К2 до пересечения с линией 2 распределения скоро-

стей колеса 2. Тогда

По картине распределения скоростей можно найти и величину передаточного отношения.

Из рисунок 3.30а видно, что

337

гдеΘ1 и Θ2 – углы, образованные линиями распределения скоро-

Знак минус поставлен потому, что углы Θ1 и Θ2 отсчитываются от базисной линии (на рисунок 3.30а – линия центров) в противоположных направлениях.

Вывод: передаточное отношение между двумя звеньями зубчатой передачи равно взятому с определенным знаком отношению тангенсов углов наклона линий распределения скоростей соответствующих звеньев из картины распределения скоростей.

Картину распределения скоростей необязательно строить на механизме. Для ее построения можно провести параллельно линии центров базисную линию, снести на нее точки П, О1, О2, … , скоростями которых или задаемся, или скорости которых известны, или будут находиться. Дальнейший порядок построения картины распределения скоростей остается прежним (рисунок 3.30б).

Передаточное отношение можно найти и по диаграмме угловых скоростей (рисунок 3.30в). Для построения этой диаграммы необходимо:

1)параллельно векторам скоростей из картины распределения скоростей провести базисную линию;

2)выбрать на базисной линии произвольный полюс “P” и из него перпендикулярно базисной линии отложить произвольное полюсное расстояние РО;

3)из точки “O” провести лучи параллельно линиям распределения скоростей до пересечения с базисной линией. Полученные на базисной линии отрезки P1 и P2 в некотором масштабе

будут изображать угловые скорости колес 1 и 2.

т.е. отрезок P1 изображает угловую скорость колеса 1, а P2 - колеса

2.

Вывод: передаточное отношение между двумя звеньями зубчатой передачи равно взятому с определенным знаком отноше-

338

нию соответствующих отрезков из диаграммы угловых скоростей.

Если изображающие точки (например, 1 и 2) расположены по разные стороны относительно полюса “P”, то передаточное отношение отрицательно, если по одну сторону – то положительно.

Если известна угловая скорость какого-либо колеса (например, 1), то масштаб диаграммы угловых скоростей находится так:

3.5.2 Примеры решения задач на определение передаточного отношения планетарных механизмов графическим способом Задача 1: определить графически передаточное отношение U1H

зубчатого механизма, показанного на рисунке 3.31а. Радиусы начальных окружностей колес известны.

Рисунок 3.31 Чертим в масштабе кинематическую схему механизма (рисунок

3.31а) и строим картину распределения скоростей (рисунок 3.31б). Для этого проводим базисную линию и задаемся скоростью точ-

ки “A”, снеся ее на базисную линию и отложив перпендикулярно к

ней в произвольную сторону произвольный отрезок Aa . Вектор Aa изображает скорость точки “A” колеса 1. На колесе 1 известна еще скорость точки “О1” , она равна нулю. Сносим точку “О1” на базис-

339

ную линию и через точки “О1” и “а” проводим линию распределения скоростей колеса 1. От колеса 1 переходим к блоку колес 2 – 3. На этом блоке известны скорость точки “А” и скорость точки “О2”. Сносим точку “О2” на базисную линию и проводим линию аО2, которая будет являться линией распределения скоростей колес 2 – 3. Затем находим скорость точки “В” колеса 3. Для этого сносим ее на

базисную линию и проводим отрезок Bb до пересечения с линией распределения скоростей колес 2 – 3.

Переходя к блоку сателлитов 4 – 5, видим, что на этих колесах известны скорости точек “В” и “С” (скорость точки “С” равна нулю, т.к. принадлежит неподвижному колесу 6). Сносим точку “С” на базисную линию и проводим линию Сb распределения скоростей колес 4 – 5. После этого можно найти скорость точки “О4” колес 4-5,

если на картине распределения скоростей провести отрезок O4 o4 до

пересечения с линией 4 – 5. Точка “О4” принадлежит и водилу “Н”, на котором известна скорость точки “ОН” (она равна нулю). Снося точку “ОН” на базисную линию и проводя прямую OH o4 , получим линию Н распределения скоростей водила.

Если известна угловая скорость ω1 колеса 1, то можно подсчитать масштаб μv картины распределения скоростей.

Построим диаграмму угловых скоростей (рисунок 3.31в). Для этого проводим линию параллельно векторам окружных скоростей из картины распределения скоростей, которая будет базисной линией.

Перпендикулярно к ней откладываем полюсное расстояние РО и из точки “O” проводим до пересечения с базисной линией лучи параллельно всем линиям распределения скоростей.

Передаточное отношение

где P1и PH - отрезки в мм, измеренные на диаграмме угловых скоростей.

Передаточное отношение получилось со знаком минус, т.к. изображающие точки 1 и H расположены по разные стороны относительно полюса “P”.

340

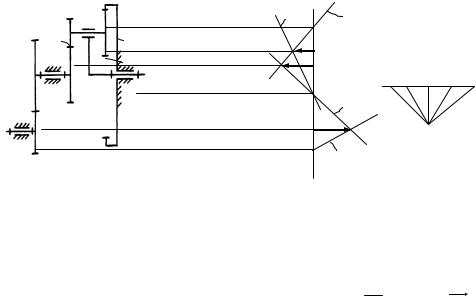
Задача 2: определить графически передаточное отношение U1δ зубчатого механизма, показанного на рисунок 3.32а. Радиусы начальных окружностей колес известны.

При построении картины распределения скоростей совсем необязательно задаваться скоростью того колеса, угловая скорость которого задана.

Следует задаваться скоростью точки такого звена, чтобы при переходе к звену с ним сопряженному, мы смогли найти на нем скорости двух точек и построить линию распределения скоростей этого звена.

Например, если задаться скоростью точки “A” колеса 1, то при переходе к звену 2 – 3 мы не сумеем построить его линию распределения скоростей, т.к. скорости точек “O2” и “B” неизвестны.

(рисунок 3.32б), задавшись скоростью точки “D” барабана. Так как барабан вращается вокруг неподвижной оси, проходящей через точку “Oδ”, то линия Оδd будет являться линией распределения скоростей барабана и колеса 7.

После этого можно построить линию распределения колеса 6, на котором известны скорости точек “D” и “O6”, и найти скорость точ-

ки “C”.

341

Зная скорости точек “C” и “O4” блока колес 4 – 5, строим линию О4с распределения скоростей этого звена и находим скорость точки

“B”.

На блоке сателлитов 2 – 3 кроме точки “B” можно найти скорость точки “O2”. Эта точка одновременно принадлежит и барабану.

Поэтому, проведя отрезок O2 o2 до пересечения с линией распреде-

ления скоростей 7, δ, находим скорость точки “O2”.

После этого проводим линию о2b, которая будет являться линией распределения скоростей колес 2 – 3, и находим скорость точки “A”.

Затем строим линию О4а распределения скоростей колеса 1. Имея картину распределения скоростей, построим диаграмму

3.6Коробки скоростей (коробки передач)

Врассмотренных выше зубчатых механизмах получают постоянное передаточное отношение между входными и выходными звеньями.

Между тем в технических приложениях часто возникает задача получения различных частот вращения выходного вала, т.е. задача ступенчатого регулирования скорости выходного вала.

Зубчатые механизмы, размещенные в отдельном корпусе (коробке), предназначенные для ступенчатого регулирования скорости выходного вала, называются коробками скоростей.

Существует большое количество конструкций коробок скоростей с различными числами ступеней регулирования, в которых используют как рядовые, так и планетарные зубчатые механизмы.

Часто встречаются конструкции, в которых изменение скорости выходного вала получают за счет сдвига вдоль одного из валов блока зубчатых колес до сцепления одного из колес с соответствующим ему колесом другого вала.

На рисунке 3.33 показана трехступенчатая коробка скоростей, в

которой изменение частоты вращения выходного вала II получают за счет смещения блока колес 1 – 1’ – 1’’ вдоль шпонки входного вала I.

342