
Учебная литература / n1
.pdf
ϕ′′ = |
|
−lBC sinϕ2 ,− x′′B +lBC cosϕ2 (ϕ2′ )+lCD cosϕ3 (ϕ3′)2 |
|
= |
||
|
|
|||||
3 |
|
lBC cosϕ2 |
,− y′B′ +lBC sinϕ2 |
(ϕ2′ )2 +lCD sinϕ3 (ϕ3′)2 |
|
|
|
|
|
|
|||
= lBC y′′B sinϕ2 −lBC2 sinϕ2 (ϕ2′ )2 −lBC lCD sinϕ2 sinϕ3 (ϕ3′)2 + x′′B lBC cosϕ2 − −lBC2 cosϕ2 (ϕ2′ )2 −lBC lCD cosϕ2 cosϕ3 (ϕ3′)2 = lBC (x′′B cosϕ2 + y′′B sinϕ2 )−
−lBC2 |
(ϕ2′ )2 −lBC lCD (ϕ3′)2 cos(ϕ2 −ϕ3 ) |
|
|
(2.71) |
|
ϕ2′′ = |
|
−(x′B′ cosϕ3 + y′B′ sinϕ3 )+lBC (ϕ |
2′ )2 cos(ϕ2 −ϕ3 )+lCD (ϕ3′)2 |
(2.72) |
|
|
lBC sin(ϕ3 |
−ϕ2 ) |
|||
|
|
|
|||
ϕ3′′ = |
|
x′B′ cosϕ2 + y′B′ sinϕ2 −lBC (ϕ2′ )2 |
−lCD (ϕ3′)2 cos(ϕ2 −ϕ3 ) |
|
(2.73) |
|
lCD sin(ϕ3 −ϕ2 ) |
||||
|
|
|
|||
При |
|
угловые ускорения звеньев 2 и 3 |
(2.74) |
|
(2.75) |
Чтобы найти ускорение точки С, необходимо продифференциро-
вать по |
|
выражения (2.61) и (2.62) |
|
|
|
|
|
(2.76)
113

(2.77)
(2.78)
Так как |
|
|
, то |
(2.79)
2.5.3Расчет двухповодковой группы 2-го вида
Вкачестве примера рассмотрим кривошипно-ползунный механизм (рисунок 2.19а), состоящий из начального механизма (1,0) и указанной выше структурной группы (2,3).
Дано: длины звеньев |
|
, смещение направляющей |
||
|
|
|
|
|
«е», размеры |
и |
. |
Определить: аналоги угловых скоростей и ускорений звена 2, аналоги скоростей и ускорений точек С и F.
114

Как обычно, кинематический анализ механизма начинают с расчета входного звена (рисунок 2.19б), показав предварительно систему координат xAy.
Расчет кривошипа описан формулами (2.14 ... 2.32).
Расчет структурной группы (2,3)
(рисунок 2.19в)
Для составления замкнутого векторного контура показываем
сначала векторы |
|
и |
|
, определяющие по- |
ложения внешних элементов группы относительно начала системы координат. Затем соединяем эти два вектора вектором
, направленным вдоль осевой линии шатуна 2.
115
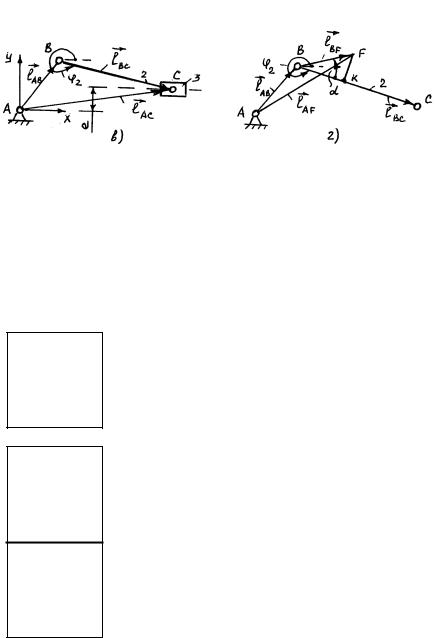
Рисунок 2.19 Уравнение замкнутости полученного векторного контура:
(2.80)
Проецируем (2.80) на координатные оси:
(2.81)
(2.82)
Из (2.82) находим
116

(2.83)
а затем
(2.84)
где коэффициент, а = ±1 в зависимости от способа сборки группы;
а = 1, если проекция вектора lBC на ось х положительна; (см.
рисунок 2.19в), а = -1, если проекция этого вектора на ось х отрицательна.
По знакам |
|
и |
|
определяют четверть, |
в которой в данный момент находится угол φ2, а затем и величину этого угла.
После этого из (2.81) находят положение ползуна С – коорди-
нату хС.
Определение аналогов скоростей
Дифференцируем уравнения замкнутости (2.81) и (2.82) по параметру φ1:
(2.85)
117

(2.86)
( |
|
|
, поэтому |
|
). |
В этих уравнениях неизвестными параметрами являются аналог
угловой скорости |
|
звена 2 и аналог скорости |
точки С. Из (2.86) определяют
(2.87)
Подставляют (2.87) в (2.85) и находят |
|
. |
|
|
|
Определение аналогов ускорений
Для этого нужно дважды продифференцировать по параметру φ1 уравнения замкнутости (2.81) и (2.82), или, что то же самое, продифференцировать (2.85) и (2.86).
118

(2.88)
(2.89)
В этих уравнениях неизвестными величинами являются аналог
углового ускорения |
|
звена 2 и аналог ускорения тос- |
ки С |
|
. |
Из (2.89) |
|
|
(2.90)
Подставляем (2.90) в (2.88) и находим
.
Определение параметров произвольной точки F звена 2
В дальнейшем произвольной точкой звена может быть любая точка звена, не вошедшая в замкнутый векторный контур группы: центр масс звена, точка присоединения последующей группы, точка приложения силы и т.д.
119

Составим векторный контур для определения параметров точки F (рисунок 2.19г).
В этот контур войдут вектор |
|
, определяющий по- |
ложение точки F относительно начала системы координат, вектор
одной из шарнирных точек звена 2 (точки B) и век-
тор |
|
|
, введенный для замыкания контура. |
Угловое положение дополнительного вектора
описывают углом |
|
|
|
дополнительного |
|
|
|
||
вектора, который |
|
|
от основного вектора |
|
отсчитывается |
||||
звена 2 (он присутствовал в уравнении замкнуто-
сти (2.80) структурной группы) против хода часовой стрелки.
Угол α можно найти из соотношения
120

(2.91)
(2.92)
Из рисунка 2.19г видно, что
(2.93)
или в проекциях на координатные оси
(2.94)
(2.95)
Дифференцируем по φ1 (2.94) и (2.95)
(2.96)
121

(2.97)
(2.98)
Дифференцируем (2.96) и (2.97)
(2.99)
(2.100)
(2.101)
2.5.4 Расчет двухповодковой группы 2-го вида
сподвижной направляющей (рисунок 2.20)
Впредыдущем случае внешняя поступательная пара (3,0) структурной группы была образована с неподвижной направляющей.
Возможны также случаи использования двухповодковой группы 2-го вида в механизмах с подвижной направляющей.
Рассмотрим кулисный механизм, показанный на рисунке 2.20а.
122
