Учебная литература / 301-001100

модели, которые корректно отображали бы все условия - в форме уравнений и неравенств, логические условия.

Кинематический анализ рычажных механизмов

Целью кинематического анализа механизмов является определение перемещений, скоростей и ускорений точек механизма и угловых скоростей и ускорений звеньев. При выполнении кинематического анализа могут определяться первая и вторая производная функции положения при заданном законе движения (входные координаты и их производные) входных звеньев. Возможно, и обратное решение, то есть определение производных входных координат по известным значениям выходных координат. Кинематические параметры, полученные в результате анализа необходимы для оценки его качества, а также для последующего силового анализа. В этой главе будет рассмотрен кинематический анализ плоских рычажных механизмов с числом

степеней свободы .

Особенностью кинематического анализа механизма состоит в том что аргументом производных кинематических функций являютcя производные обобщенной координаты. Дадим основные определения.

Рис. 9

Передаточные кинематические функции Линейная функция положения точки это зависимость проекций точки на оси координат в зависимости от обобщенной координаты (рис.9)

Зависимость угловой координаты какого-либо звена механизма от обобщенной координаты – угловая функция положения данного звена.

Первая производная линейной функции положения точки по обобщенной координате – линейная передаточная функция точки (аналог линейной скорости)

Первая производная угловой функции положения звена по обобщенной координате называется передаточное отношение.

Вторая производная линейной функции положения по обобщенной координате – аналог линейного ускорения точки в проекциях на соответствующие оси.

21

Вторая производная угловой функции положения звена по обобщенной координате – аналог углового ускорения звена.

Кинематические функции и их аналоги связаны следующими соотношениями:

Методы кинематического анализа Определение кинематических параметров может проводиться различными методами:

аналитическими, графоаналитическими и графическими. Эти способы определения кинематических параметров отличаются объемом работ по выполнению анализа и точностью. В настоящее время в основном используются аналитические методы, вследствие их принципиальной точности и простой адаптации к использованию на компьтере. Рассмотрим один из аналитических способов для кулисного механизма, изображенного на Рис. 9

Метод проекций векторного контура

Рис. 9

Заменим кинематическую схему механизма эквивалентным векторным контуром (Рис.

10)

22

Рис. 10

Векторное уравнение замкнутого контура запишется:

+

Определение положений точек и звеньев кулисного механизма Проецируя векторный контур на оси координат получаем координаты точки В механиз-

ма:

Положение механизмов определяет значение угла и определить которые

можно из уравнений приведенных выше

Вычисление передаточных функций механизма Продифференцируем уравнения проекций векторного контура по обобщенной коор-

динате и получим

Находим и кинематические функции находятся по приведенным выше зави-

симостям.

Найдем вторую производную от проекций уравнения векторного контура на координатные оси.

23

Из этой системы уравнений определяем вторые передаточные функции и

Метод планов

Этот способ определения кинематических параметров наиболее часто использовался в недавнее время. По точности определения кинематических параметров он уступает аналитическим методам, но для большинства практических задач его использование оправдано простотой использования. По этому методу аналитически составляются векторные уравнения, а решаются графически. План положений механизма (кинематическая схема) – чертеж на котором в мас-

штабе изображены мгновенные положения механизма.

( )

План скоростей (ускорений)-чертеж, на котором в масштабе изображены отрезки сов-

падающими по направлению с векторами скоростей или ускорений точек механизма. Отрезки, отображающие абсолютные скорости и ускорения, начинаются в точке называемой полюс плана. Относительные движения не проходят через полюс.

План скоростей обладает следующими свойствами:

-отрезок, соединяющий концы векторов скоростей любых двух точек тела, перпендикулярен отрезку, соединяющему соответствующие точки тела;

-длины отрезков, соединяющих концы векторов скоростей точек тела, пропорциональны длинам отрезков, соединяющим соответствующие точки.

При проведении кинематического анализа методом планов предполагается что , то есть движение начального звена равномерное.

Проведем кинематический анализ для мгновенного положения кривошипно-ползунного механизма приведенного на рис 1.9. Известны следующие величины - , .Требуется определить - , , ,

Определение скоростей точек и звеньев механизма Выберем масштаб для плана положения механизма

Определим скорость точки – А × ,

Найдем скорость точки – В, совершающей плоско-параллельное движение. C использованием теоремы сложения движений по которой = .Для плана скоростей

24

реносная скорость.

=

=

Первое векторное уравнение на плоскости содержит три неизвестных (модуль и направление вектора ) и поэтому необходимо записать дополнительное уравнение

из которого следует что = так как =0, то есть скорость направлена перпендикуляр-

Измерив отрезки можно определить кинематические параметры:

, , , =

25

Рис.11

Определение ускорений точек и звеньев механизма методом планов.

Поскольку принято допущение о равномерном движении начального механизма, то

и

Ускорение точки направлено к центру вращения- O.Ускорение точки –B определим из системы векторных уравнений

=

=

Ускорение = AB= . Из второго уравнения следует что = , по-

скольку направляющие ползуна неподвижны и прямолинейны. Ускорение S определим из пропорции.

Выберем масштаб плана ускорений

где отрезок отображающий ускорение Построим план ускорений (Рис.12), из произвольно выбранного полюса π проведем отрезок , параллельно OA и направленный к точке O.К концу отрезка и направленный от точки В к А параллельно шатуну АВ на плане положений механизма. К концу отрезка на чертеже проведем линию перпендикулярную шатуну

АВ (отрезок направлен как ).Из полюса плана ускорений проведем линию параллельную

направлению .На пересечении этих отрезков и будет находится точка b являющаяся кон-

26

цом отрезка , являющимся отображением в масштабе .Конец отрезка ,точка ,определяется аналогично построению плана скоростей.

Рис.12

Измерив отрезки можно определить ускорения точек механизма :

, , =

Графический метод кинематического анализа

Данный метод дает наглядное представление об изменении кинематических параметров. При выполнении исследования “ вручную” точность способа ниже, чем у графо - аналитического метода, однако при использовании компьютере можно получить любую наперед заданную точность. Способ преимущественно используется, если кинематические параметры записаны приборами и по этим данным построен график функции. Используя графическое дифференцирование или интегрирование получают производные или первообразные от функции изображенной на графике.Графическое дифференцирование осуществляется методом хорд и касательных. Рассмотрим метод хорд (Рис.13).

27

Рис. 13

Метод касательных, разработанный И.Ньютоном , основан на том, что приращение бесконечно малого приращения функции к бесконечно малому приращению аргумента, то есть производная представляет тангенс угла наклона касательной к кривой в точке определения производной и тогда

Для того чтобы провести касательную к точке необходимо определить центр кривизны кривой на этом этапе возникают погрешности, и метод касательных используется редко.

Метод хорд предполагает, что в середине отрезка определения функции

и вместо касательной к точке проводится хорда. Значение производной определяются посредине участка на котором проводится хорда.

Рассмотрим графическое дифференцирование методом хорд на примере графика приведенному на Рис. 13 в следующей последовательности:

-разделим ось абсцисс на интервалы(не обязательно равные); -соединим хордами минимальные и максимальные значения функции на этих участках;

-отступив влево от начала координат графика (необходимо, если требуется определенный масштаб графика производной) получим точку B;

-из точки В проводим лучи параллельные хордам до пересечения с осью ординат графика , то есть отрезок Ba параллелен ходе участка 01, Bb параллелен ходе участка 12 и так далее;

-от точки пересечения луча с осью ординат проводим отрезки до середины участка, на котором проведена хорда;

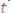
- соединив полученные точки получим график производной , масштаб полу-

ченного графика .

28

При графическом интегрировании подинтегральная функция задается графиком. Рассмотрим определение угла поворота по кривой , полученной при

эксперименте. График угловой скорости выходного звена построен по экспериментальным данным в масштабе угловой скорости и времени (Рис.14).Интегрирование в рассматривае-

мом методе идентично методу хорд выполненному в обратном порядке.

Выполним графическое интегрирование методом площадей кривой (рис. 14) в следуюшем порядке

-разделим ось абсцисс на интервалы (не обязательно равные); - определим значение функции на середине интервала;

-проведем параллельные оси абсцисс отрезки до пересечения с осью ординат где полу-

чим точки a,b,c,d,e,f,g,h;

-продолжим ось абсцисс влево и отложим на ней точку В на расстоянии ВО;

-соединим точку В с точками пересечения отрезков с осью абсцисс, получим лучиBa,

Bb, Bc, Bd, Be, Bf, Bg, Ba ;

-проведем линии параллельные лучам Ba, Bb, Bc, Bd, Be, Bf, Bg, Ba на расположенном ниже графике складывая конечную точку предыдущего луча с начальной точкой последующего;

- полученная ломаная линия будет являться графиком в масштабе

.

Рис. 14

29

Силовой анализ механизмов

После проведения структурного и кинематического анализа механизма следующая ступень расчета заключается в определении сил действующих в механизме. Полностью силовой анализ может быть проведен только после окончательной разработки, когда известны массы и моменты инерции звеньев, а также известны величины сил трения в кинематических парах. На первом этапе при еще не законченной разработке исследование проводится по упрощенной модели, когда из всех сил, действующих на механизм, учитываются обобщенные движущие

силы Q, рабочие нагрузки и , реакции связей и а также силы и моменты сил инер-

ций звеньев. Уравнения динамики для этой модели являются по существу уравнениями статики. Но анализ проводится для различных мгновенных положений механизма и силы определяются при наличии следующих условий:

-закон движения начальных звеньев или звена известен и движение равномерное, -известны внешние силы действующие на механизм, -механизм в плоскости статически определим

При этом определяются уравновешивающие силы, которые необходимо приложить к входному звену, чтобы уравновесить рабочие усилия и инерционные нагрузки. Если силы инерции звеньев малы (механизм тихоходный) и не учитываются, расчет является статическим. При учете сил инерции при расчете метод является кинетостатическим. Дополнительно определяются реакции в кинематических парах необходимые для определения размеров звеньев и кинематических пар. В некоторых случаях, когда не требуется определять реакции, может использоваться принцип возможных перемещений (рычаг Жуковского).

Кинетостатический расчет механизма

Кинетостатический расчет механизма может осуществлятся графоаналитическим и аналитическим способом но в их основе лежит принцип Д'Аламбера согласно которому если ко всем внешним силам действующим на механизм добавить силы инерции получим статически определимую систему. Для каждого звена механизма можно записать три уравнения равновесия.

Где-

внешняя сила. Уравнения проекций сил на координатные оси могут быть заменены одним векторным уравнением

Главный вектор и главный момент определяются по следующим зависимостям

Где -масса звена, – момент инерции относительно центра масс.

Предполагается что главный вектор приложен в центре масс, знак минус в уравнениях показывает, что сила инерции направлена в противоположную сторону ускорения центра масс

звена- , а главный момент направлен в сторону противоположную угловому ускорению звена- .

30