Учебная литература / 1_6

геометрическое подобие треугольников О1М1С и Сυ1υN1, а также треугольников О2М2С и Сυ2υN2, получим:

; .

Если υN1¹υN2, то профиль П1 либо должен проникнуть в профиль П2, либо отстать от него, что исключается. Из равенства этих составляющих:

ω1 × О1М1= ω2 О2М2,

следует

.

Из подобия треугольников О1М1W и О2М2W:

.

Окончательно имеем

. (1.82)

Соотношение (1.82) выражает основной закон зацепления: общая нормаль N-N к профилям,

проведенная в точке C их касания, делит межосевое расстояние аw на части, обратно

пропорциональные угловым скоростям. При постоянном передаточном отношении (= const) и зафиксированных центрах О1 и О2 точка W будет занимать на линии центров неизменное

положение. При этом проекции скорости υk1 и υk2 не равны. Их разность указывает на относительное скольжение профилей в направлении касательной К-К, что вызывает их износ.

Равенство проекций скоростей и возможно только в одном положении, когда точка С контакта профилей совпадет с точкой W пересечения нормали N-N и линии центров​ О1О2. Точка W

называется полюсом зацепления, а окружности с диаметрами dw1 и dw2, которые касаются в

полюсе зацепления и перекатываются друг по другу без скольжения, называются начальными. Для обеспечения постоянства передаточного отношения теоретически один из профилей

может быть выбран произвольно, но форма профиля сопряженного зуба должна быть строго определенной для выполнения условия (1.82). Наиболее технологичными в изготовлении и эксплуатации являются эвольвентные профили. Существуют и другие виды зацепления: циклоидальное, цевочное, зацепление Новикова, удовлетворяющие данному требованию.

1.6.2. Классификация зубчатых передач

Передачи классифицируют по геометрическим и функциональным особенностям:

·по характеру расположения валов: цилиндрические (рис. 1.33, а, б, в, г) – имеют параллельные оси; конические (рис. 1.33, е, ж, з) – имеют пересекающиеся оси; гиперболоидные, винтовые,

гипоидные – передачи со скрещивающимися осями. Для преобразования вращательного движения

впоступательное, и наоборот, применяют реечную передачу (рис. 1.33, д). Ее можно рассматривать как частный случай цилиндрической зубчатой передачи, у которой диаметральные размеры одного из колес (рейка) увеличены до бесконечности.

·по форме профилей зубьев: эвольвентные (рабочие профили очерчены эвольвентами окружностей), циклоидальные (профили – дуги эпициклоиды и гипоциклоиды), передачи Новикова (профили – дуги окружностей) и др.;

·по расположению зубьев относительно образующих основной поверхности – прямозубые

(рис. 1.33, а, г, д, е), косозубые (рис. 1.33, б, ж), шевронные (рис. 1.33, в), криволинейные (рис. 1.33, з);

·по расположению осей колес относительно точки касания профилей – передачи внешнего (рис. 1.33, а) и внутреннего зацепления (рис. 1.33, г);

Рис. 1.33. Виды зубчатых передач

∙по характеру движения осей: одно- и многоступенчатые обычные передачи, имеющие неподвижные геометрические оси всех колес; сателлитные передачи (дифференциальные, планетарные), у которых имеются оси одного или нескольких колес (сателлитов), движущиеся по круговым траекториям;

∙по конструктивному исполнению передачи могут располагаться вне корпуса (открытые) либо работать в корпусе, который изолирует их от внешней среды (закрытые).

1.6.3. Основы теории эвольвентного зацепления

Из множества кривых, удовлетворяющих требованиям основного закона зацепления, наибольшее практическое применение в современном машиностроении получили эвольвентные профили. В общем случае эвольвентой называют плоскую кривую, являющуюся разверткой другой плоской кривой – эволюты. Для образования профилей зубьев колес в качестве эволюты

используют окружность, называемую основной ( – радиус основной окружности). Эвольвенту этой окружности будет описывать любая точка производящей прямой N-N, перекатывающейся по ней без скольжения (рис. 1.34).

Угол развернутости эвольвенты между нормалями к эвольвенте в ее предельной, принадлежащей основной окружности, и рассматриваемой точках равен соотношениям:

где α – профильный угол эвольвенты (угол давления), т.е. угол между текущим радиусом –

вектором и касательной К-К к эвольвенте в точке , равный углу между радиусом – вектором и радиусом ОМ основной окружности, проведенным в точке М касания производящей прямой.

Функцию Θ угла α называют эвольвентной функцией или инволютой, ее используют при геометрическом расчете эвольвентных профилей.

Из способа образования эвольвенты следует:

∙эвольвента не может существовать внутри основной окружности и имеет две ветви в зависимости от направления вращения производящей прямой N-N;

∙две одноименные эвольвенты являются эквидистантными кривыми, т.е. расстояние между ними, измеренное по любой общей нормали, одинаково и равно спрямленной дуге основной окружности между началами эвольвент;

∙нормаль, проведенная в любой точке эвольвенты, является касательной к основной окружности;

∙радиус кривизны эвольвенты в любой точке равен длине касательной от этой точки до основной окружности.

Если основную окружность заменить основным цилиндром с радиусом rb (рис. 1.35, а), а прямую АВ – плоскостью Н, то при обкатке ее без скольжения по основному цилиндру прямая АА′, параллельная образующей основного цилиндра ВВ′, опишет эвольвентную поверхность прямого зуба. Если на плоскости Н взять прямую АА′′, расположенную под углом βb к образующей

основного цилиндра, то при обкатке эта прямая образует винтовую поверхность, которая используется в качестве рабочей поверхности зуба косозубого цилиндрического колеса.

Боковые поверхности зубьев конического колеса образуются подобно эвольвентным цилиндрическим, но вместо основного цилиндра производящая плоскость обкатывается по основному конусу (рис. 1.35, б).

Если профили зубьев двух колес, очерченные эвольвентными Э1 и Э2 (рис. 1.36), касаются в точке К, то общая нормаль N1-N2 в точке контакта профилей будет касательной к обеим основным окружностям. При вращении колес точка касания профилей переместится в точку К1, но общая

нормаль по-прежнему будет касаться основных окружностей, т.е. ее положение останется неизменным. Неизменным остается и положение полюса W на межосевой линии О1О2. При вращении

колес точка контакта профилей будет всегда находиться на прямой N1 -N2, являющейся общей нормалью к профилям.

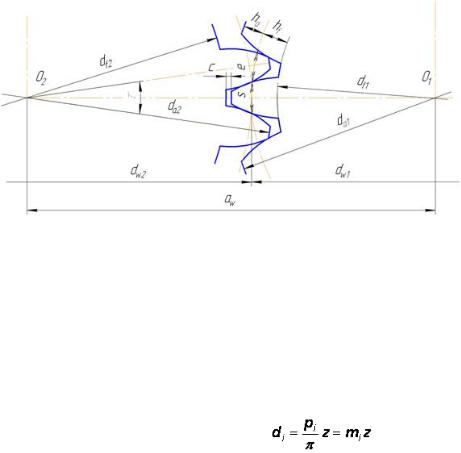
При изменении межосевого расстояния аw линия зацепления изменяет свое положение, при этом изменяется и угол зацепления αw, но сопряженность зубьев и величина передаточного

отношения не нарушаются.

Таким образом, эвольвентное зацепление обеспечивает постоянство передаточного отношения, т.е. является кинематически точным.

Давление одного эвольвентного профиля на другой, передаваемое по общей нормали (линию N-N называют также линией давления), сохраняет постоянное направление в пространстве в течение всего периода зацепления профилей.

Зубья располагаются на ободе зубчатого колеса вблизи начальной окружности. Как видно из рис. 1.37, часть профиля зуба выполнена за пределами начальной окружности, а часть – внутри ее. Со стороны тела зубчатого колеса зубья отделяются окружностью впадин диаметра df, а с

противоположной стороны – окружностью вершин диаметра dа. Часть зуба высотой hа,

расположенная между начальной окружностью и окружностью вершин, называют начальной вы-​ сотой головки зуба, а часть зуба hf, заключенная между начальной окружностью и окружностью

впадин, – начальной высотой ножки зуба. Наименьшее расстояние с между окружностью вершин одного колеса и окружностью впадин другого называют радиальным зазором передачи.

Рис. 1.37. Зацепление эвольвентной цилиндрической передачи с колесами, нарезанными без смещения

Центральный угол τ = 2π/z, где z – число зубьев, называется угловым шагом. Дуга окружности, вмещающая один зуб (без впадины), носит название окружной толщины зуба s. Расстояние е по дуге окружности между двумя соседними зубьями называют окружной шириной впадин. Расстояние между одноименными профилями двух соседних зубьев, измеренное по дуге окружности, называют окружным шагом p зубьев. Толщину зуба, ширину впадины и шаг можно измерить по любой окружности. Для любой концентрической окружности диаметром di

справедливо равенство , откуда

где pi – окружной шаг зубьев, измеренный по окружности диаметром di.

Отношение окружного шага pi к числу π называется окружным модулем зубьев: .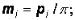

Окружной модуль, так же, как и окружной шаг, имеет различные значения для различных концентрических окружностей. Однако на каждом зубчатом колесе имеется окружность, для которой модуль соответствует стандартному (ГОСТ 9563-60) значению. Эта окружность является базовой для определения размеров элементов зубьев и называется делительной (d – диаметр делительной окружности). Делительный модуль m (модуль) – основной параметр, используемый для геометрического расчета зубчатого колеса с заданным числом зубьев.

Если диаметральные размеры колес стремятся к бесконечности, окружности обращаются в прямые линии, а само колесо превращается в рейку. При работе реечной передачи одна из прямых рейки (средняя прямая m-m) перекатывается без скольжения по начальной окружности колеса. Соответственно, по этой окружности окружной шаг равен шагу рейки. Согласно свойствам

эвольвенты профиль зуба рейки прямобочный, трапециевидной формы, с углом заострения . Зацепление эвольвентного зубчатого колеса с рейкой положено в основу нарезания зубчатых

Теоретически максимальное значение коэффициента перекрытия для прямозубых колес =1,98, т.е. в зоне полюса (точка W) существует область однопарного зацепления.

Значение коэффициента перекрытия определяют через параметры зубчатых колес на основании картины зацепления:

, (1.92)

где αw – угол зацепления передачи; , , – соответственно радиусы окружностей вершин и основных окружностей зубчатых колес:

; .

(1.93)

; .

1.6.4. Силы, действующие в зацеплении

В косозубой цилиндрической передаче, нагруженной крутящим моментом Т1 на валу шестерни

(шестерней называют меньшее из двух зубчатых колес), по линии зацепления (рис. 1.39) действует сила Fn нормального давления, которую можно разложить на окружную Ft, радиальную Fr и

осевую составляющие, связанные зависимостями:

В конической прямозубой передаче (рис. 1.40) составляющие полного нормального усилия Fnm, рассчитываемые по среднему диаметру dm, следующие:

(1.96)

где δ – угол при вершине начального конуса колеса передачи с углом пересечения осей 90°.

1.6.5. Особенности геометрии косозубых цилиндрических передач

У косозубых колес зубья составляют с образующими делительного цилиндра угол β. Для нарезания зубьев используют инструмент такого же исходного контура, как и для нарезания прямых зубьев. Поэтому профиль косого зуба в нормальном сечении n-n (рис. 1.41) совпадает с профилем прямого зуба. Модуль mn в этом сечении должен соответствовать стандартному

значению. Размеры колес удобно измерять в торцовом сечении t-t. Соответственно, делительный диаметр колеса

. (1.97)

Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в нормальном сечении принято выражать через параметры эквивалентного прямозубого колеса (рис. 1.41). Нормальное к зубу сечение образует эллипс с полуосями: с=0,5d и е=0,5d/cosβ. В зацеплении участвуют зубья, расположенные на малой оси эллипса, так как второе колесо находится на расстоянии с = 0,5 d. Радиус кривизны эллипса на малой оси

.

Рис. 1.41. Определение параметров эквивалентного колеса

В соответствии с этим форма косого зуба в нормальном сечении совпадает с формой зуба эквивалентного прямозубого колеса, делительный диаметр которого

(1.98)

и число зубьев

. (1.99)

С увеличением угла наклона линии зуба эквивалентные параметры возрастают, способствуя повышению прочности передачи.

Благодаря наклону зубьев возрастает суммарная длина линии контакта

увеличивается относительная продолжительность зацепления, характеризуемая коэффициентом εβ осевого перекрытия:

.

В общем случае непрерывность зацепления косозубых передач обеспечивается, если общий коэффициент перекрытия ε =(εα+εβ) ³1. В зацеплении косозубых колес всегда имеется

возможность получать сравнительно большие значения ε. Благодаря этому зубья нагружаются постепенно, по мере захода их в поле зацепления, передачи работают более плавно, менее шумно и с меньшими динамическими нагрузками по сравнению с прямозубыми.

Контрольные вопросы

1.Каковы основные достоинства и недостатки зубчатых передач по сравнению с другими передачами?

2.По каким признакам классифицируют зубчатые передачи?

3.В чем сущность основной теоремы зацепления?

4.Что такое эвольвента окружности, какими свойствами она обладает?

5.Какие окружности зубчатой передачи называются начальными и делительными?

6.Какой параметр называют модулем, цель его стандартизации?

7.Что понимают под коэффициентом торцового перекрытия? Как влияет его величина на работу зубчатой передачи?

8.В чем проявляются достоинства и недостатки косозубой цилиндрической передачи по сравнению с прямозубой?