Добавил:

lowwro Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский технический университет связи и информатики

Предмет:

Математические пакеты

Файл:

ВМиППП-Лабораторные(заочн)

.pdf

Скачиваний:

Добавлен:

11.02.2023

Размер:

1.54 Mб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

Тема 2. Лабораторная работа Методы решения нелинейных уравнений

2.1.Вопросы, подлежащие изучению

1.Постановка задачи численного решения нелинейных уравнений.

2.Этапы численного решения уравнения.

3.Аналитический и графический методы отделения корней.

4.Уточнение корня методами половинного деления, итерации, Ньютона и хорд.

5.Графическая иллюстрация методов половинного деления, итерации, Ньютона и хорд.

6.Условие окончания вычислений при использовании методов половинного деления, итерации, Ньютона и хорд.

7.Сходимость метода итерации, выбор начального значения корня, правило выбора итерирующей функции и оценка погрешности метода итерации.

8.Теорема о сходимости метода Ньютона и оценка погрешности метода.

9.Правило выбора неподвижной точки, начальной точки и условие сходимости метода хорд.

10. Условия окончания вычислений в методах итерации, Ньютона и хорд.

11.Сравнение методов половинного деления, итерации, Ньютона и хорд.

12.Алгоритмы и программы решения нелинейных уравнений на языке программирования.

13.Решение нелинейных уравнений средствами математических пакетов

2.2.Задание

1.Выбрать индивидуальное задание (нелинейное уравнение) из таблицы.2-1.

2.Отделить корни уравнения.

3.Уточнить корень уравнения 4-мя численными методами, для чего провести исследование нелинейного уравнения для каждого метода:

проверить выполнение условий сходимости вычислительного процесса, в случае расходящегося процесса – сделать необходимые преобразования для обеспечения сходимости;

выбрать начальное приближение;

сформулировать условия окончания этапа уточнения корня.

4.Провести «ручной расчет» трех итераций.

5.Оценить погрешность результата «ручного расчета».

6.Решить нелинейное уравнение средствами математического пакета.

Тема1.2.Методы решениянелинейных уравнений (Лабораторныйпрактикум)

Страница 1

2.3. Варианты задания

										Таблица 2-1
№	Уравнение			№	Уравнение
1	tg(0,36x +0,4) = x2			19	ex + ln(x) – x = 0
2	x + ln(4x) – 1 = 0			20	1–x+sin(x)–ln(1+x) = 0
3	ex – 4 e-x – 1 = 0			21			– cos(1–x) = 0
						1 x
4	x ex – 2 = 0			22	sin(x2)+cos(x2)–10x = 0
5	4 (x2 + 1) ln(x) – 1 = 0			23	x2 – ln(1 + x) – 3 = 0
6	2 – x – sin(x / 4) = 0			24	cos(x / 2) ln(x – 1) = 0
7	x2 + ln(x) – 2 = 0			25	cos(x/5)					– x = 0
									1 x
8	cos(x)–(x + 2)1/2 + 1 = 0			26	3x – e-x = 0
9	4 (1 + x1/2) ln(x) – 1 = 0			27	4(1+
								x) ln(x)–10 = 0
10	5 ln(x) –			28	(x-3)2 lg(x-2) = -2
			x = 0
11	ex + x3 – 2 = 0			29	x – 1 / (3 + sin(3.6x)) = 0
12	3 sin (			30	0.25x3 + cos(x / 4) = 0
		x) + x – 3 = 0
13	0.1x2 – x ln(x) = 0			31	2 – x = ln x
14	cos(1 + 0.2x2) – x = 0			32	x2 + 4sinx = 0
15	3 x – 4 ln(x) – 5 = 0			33	0,5x -3 = (x+2)2
16	sin(1 – 0.2x2) – x = 0			34	1 + lgx = 0,5
17	ex – e-x – 2 = 0			35	2 lgx – x/2+ 1 = 0
18	x – sin(1 / x) = 0			36	x – sinx = 0,25

2.4.Содержание отчета

1.Индивидуальноезадание (уравнение, метод решения).

2.Результаты этапа отделения корней (интервалы изоляции корня уравнения).

3.Результаты исследования задания для «ручного расчета»:

условие сходимости вычислительного процесса;

начальное приближение;

условие окончания процесса уточнения.

4.Результаты «ручного расчета», представленные по форме табл. 2.-2а для метода половинного деления или по форме табл. 2.-2б для остальных методов.

						Таблица 2-2а
к	a	b	f(a)	f(b)	(a+b)/2	f( (a+b)/2)	b-a
1
2
3
4

		Таблица 2-2б
к	x	f(x)

5. Оценкипогрешностей результатов «ручного расчета».

6. Результаты решения задачи, полученные с помощью математического пакета. Страница 2

Тема1.2.Методы решениянелинейных уравнений (Лабораторныйпрактикум)

2.5.Пример выполнения задания

1.Задание для решения нелинейных уравнений:

уравнение f(x) 1 3x cosx 0;

методы решения нелинейных уравнений для ручного расчета – половинного деления, итерации, Ньютона и хорд;

2.Отделение корней с использованием MathCad

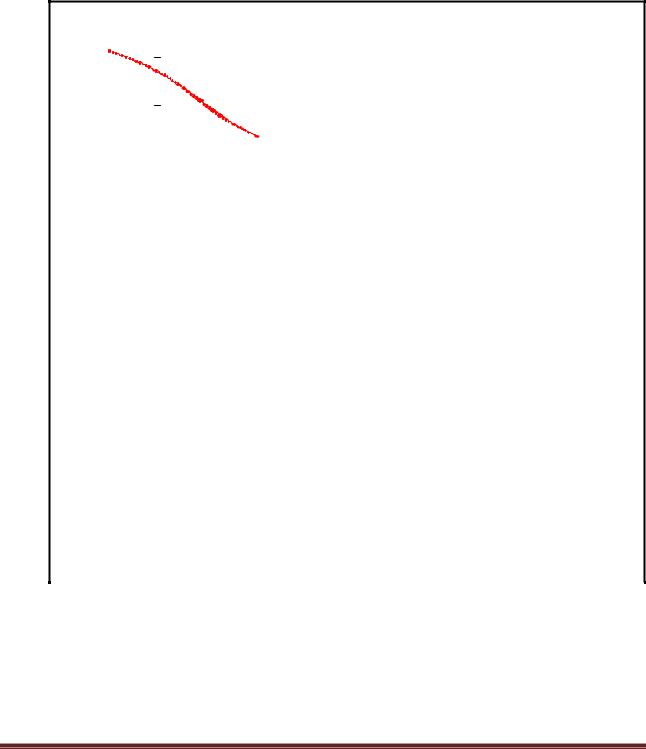
Отделение корней производим графическим методом (а) с обязательным подтверждением результата аналитически (б)

а)

f (x) 1 3x cos(x)

							10
							10
									5






f(x)		2						5			0			2		4



						10


						15						x
						15

f1(x) d			f (x)							sin(x)					3
	dx
f2(x)		d	2		f (x) cos(x)
		d
				2
		dx
x 0 0.1 1
x				f(x)									f1(x)				f2(x)

0							2							-3			-1

0.1							1.695							-3.1			-0.995

0.2							1.38							-3.199			-0.98

0.3							1.055							-3.296			-0.955

0.4							0.721							-3.389			-0.921

0.5							0.378							-3.479			-0.878

0.6							0.025							-3.565			-0.825

0.7				-0.335										-3.644			-0.765
0.8				-0.703										-3.717			-0.697

0.9				-1.078										-3.783			-0.622

1							-1.46							-3.841			-0.54

б) На отрезке [0; 1] функция f(x) меняет знак, т.е. существует, по крайней мере, один корень. Поскольку знак первой производной f1(x)= -sin(x) - 3 < 0 на выбранном отрезке остается постоянным, то можно сказать, что функция на этом отрезке монотонна. Знакопостоянство второй производной f2(x)= -cos(x)<0 на выбранном отрезке является необходимым условием применения метода Ньютона и метода хорд. Следовательно, уравнение 1-3х+cos(x)=0 имеет единственный корень на отрезке [0;1].

Тема1.2.Методы решениянелинейных уравнений (Лабораторныйпрактикум)

Страница 3

3.Уточнение корня с использованием MathCad

Метод половинного деления

1) Исследование задания

Метод половинного деления сходится, если на выбранном отрезке отделен один

корень. Так как на отрезке [0;1] функция f(x) 1 3x cosx 0 меняет знак (f(0) f(1) 0) и монотонна (f’(x)<0), то условие сходимости выполняется.

Выберем за начальное приближение середину отрезка	x	0	a b	=0.5.
		0	2

Условие окончания процесса уточнения корня. Для оценки погрешности метода половинного деления справедливо условие |bn – an|<ε , т.е. длина отрезка, полученного на n-ом шаге должна быть меньше заданной точности - b2na

2)Результаты «ручного расчета» трех итераций

f(x) 1 3x cos(x)

1 итерация

a 0

b 1

x0 0.5

f(x0)=0.377

f(a)>0,

f(x0)>0 и f(b)<0

следовательно, a1 x0

b1 b

2 итерация

a1 b1

a1 0.5

1 x1

x1 0.75

f(x1)=-0.518

f(a)>0,

f(x1)<0 и f(b)<0

следовательно,

a2 a1

b2 x1

3 итерация

a2 0.5

0.75

a2 b2

x2 0.625

f(x2)=-0.064

f(a)>0,

f(x2)<0 и f(b)<0

следовательно,

a3 a2

b3 x2

и т.д.

Результаты вычислений представлены в форме табл. 2-2а.

f(a)

f(b)

(a+b)/2

f( (a+b)/2)

b-a

-1.459

0.5

0.377

0.5

0.377

-1.459

0.75

-0.518

0.25

0.5

0.75

0.377

-0.518

0.625

-0.064

0.125

0.5

0.625

0.377

-0.064

0.5625

0.158

0.0625

После трех итераций приближение к корню – середина отрезка x3=0.5625.

3) Погрешность численного решения нелинейных уравнений

Оценим погрешность результата после трех итераций

b3 a3

0.125.

Страница 4

Тема1.2.Методы решениянелинейных уравнений (Лабораторныйпрактикум)

Метод итераций

1) Исследование задания для «ручного расчета»

Приведем

уравнение

f(x)=0

к виду x (x). Тогда

рекуррентная формула

xn 1 (xn),

n 0,1,....

Для сходимости процесса итерации необходимо, чтобы

'(x)

при x [a;b]. Если

'(x)

1, то сходимость не обеспечена.

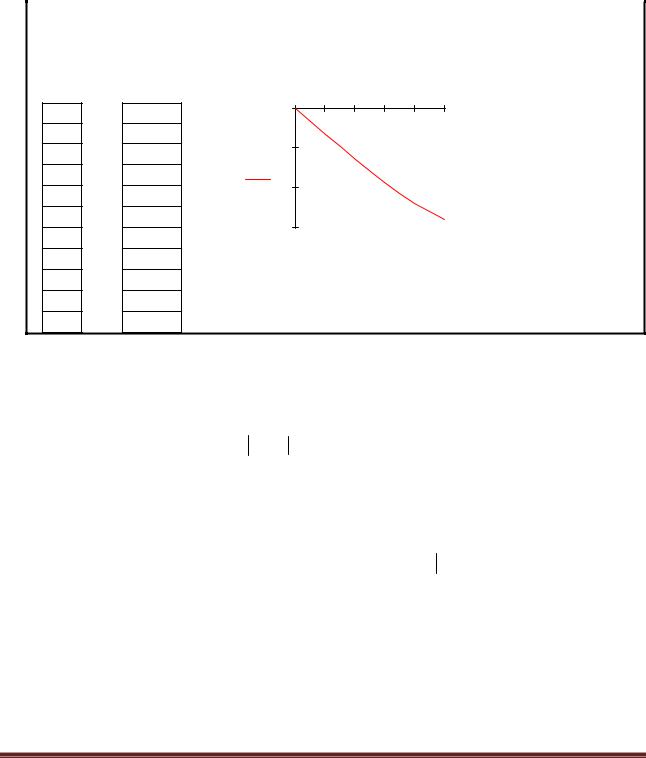
Приведем

уравнение f(x) 1 3x cosx 0 к виду x =

(cos(x)+1)/3 и проведем

исследование.

(x)

1 cos(x)

' (x) d (x)

x 0 0.1 1

' (x)

0	0	0	0.2	0.4	0.6	0.8	1
0.1	-0.033	0	0.2	0.4	0.6	0.8	1
0.1	-0.033
0.2	-0.066	0.1
0.3	-0.099	' (x)
0.3	-0.099	0.2
0.4	-0.13	0.2
0.4	-0.13
0.5	-0.16	0.3
0.6	-0.188	0.3
0.6	-0.188
0.7	-0.215				x
0.8	-0.239	'(x)<1 для всех значений аргумента
0.9	-0.261	'(x)<1 для всех значений аргумента
0.9	-0.261	на отрезке [0,1]
		на отрезке [0,1]

1-0.28

Вприведенном примере условие сходимости выполняется и можно использовать

итерирующую функцию	(x)	1 cosx	в рекуррентной формуле для уточнения корня
		3

методом итераций, что и будет показано ниже. Однако, в случаях, когда свободный х выразить не удается, или когда '(x) 1, целесообразно воспользоваться следующим

приемом, позволяющим обеспечить выполнение условий сходимости.

Построим функцию (x) λf(x) x, где параметр λ может быть определен по правилу:

если f (x) 0,то

λ 0;

если f (x) 0,

то 0 λ

где r max(

f (a)

;

f (b))

x [a;b]

Приведем пример выбора параметра λ и итерирующей функции. Для заданного уравнения f(x) 1 3x cosx 0исследовано, что

f `(x)<0, тогда 0 1.
r
f `(0)= -3, f `(1)=-3.841,
r =max{ \|-3\|, \|-3.841\| }=3.841, тогда 0<λ<0.26.
Полагаем λ=0.25. Тогда рекуррентная формула xn+1 = φ(xn),
где φ(x)= 0.25(1 - 3x + cos x) + x = 0.25(1+x+cos x).	Страница 5
Тема1.2.Методы решениянелинейных уравнений (Лабораторныйпрактикум)	Страница 5

Выберем начальное приближение к корню (в методе итераций x0 – произвольное значение из отрезка [a;b]), например, x0=0, и с использованием итерационной

функции φ(x) (cos(x) 1)/3 выполним три итерации.

Условие окончания процесса уточнения корня. Для оценки погрешности метода итерации справедливо соотношение:

xn x* 1 qq xn xn 1 . Процесс итерации следует продолжать до тех пор, пока не

выполнится условие останова:

1 q , где q=max |φ `(x)| на выбранном

отрезке,

ε – заданная точность.

Так

как q=

(1)

=0.28, условие останова будет

xn xn 1

2.571 . Если q<1/2,

то можно использовать условие

xn xn 1

2) «Ручной расчет» трех итераций

Для получения решения уравнения методом итерации необходимо воспользоваться

следующей рекуррентной формулой:					x	n 1	1 cos(xn ) ,	x	0
						n 1	3	0
							3
(x)		1 cos(x)
(x)
			3
f(x) 1			3x cos(x)
x0	0			f (x0) 2
x1	(x0)		x1 0.667	f (x1) 0.214
x2	(x1)		x2 0.595	f (x2) 0.042
x3	(x2)		x3 0.609	f(x3) 7.95 10 3

Результаты вычислений представлены в форме табл. 2-2b.

к	Xк	f(xк)
0	0	2
1	0.6667	-0.2141
2	0.5953	4.21 • 10-2
3	0.6093	-7.9496 • 10-3

3) Погрешность численного решения нелинейного уравнения

Оценим погрешность результата после трех итераций: x * x3 1qq x3 x2 0.280.72 0.014 0.0054 .

Тема1.2.Методы решениянелинейных уравнений (Лабораторныйпрактикум)

Страница 6

Метод Ньютона

1) Исследование задания для «ручного расчета»

Необходимые и достаточные условия сходимости метода Ньютона:

f (x)непрерывна на [a;b]

и f (a) f (b) 0;

f (x) и

f (x)отличны от нуля и сохраняют знаки для x [a;b].

В нашем случае на отрезке [0;1] требования теоремы выполняются.

Начальное приближение

должно удовлетворять условию: f (x0) f (x0) 0,

т.е. за начальное приближение следует принять тот конец отрезка, где знак

функции и знак второй производной совпадают. Поскольку

f (x) < 0 и

f (1) < 0, то

выберем начальное приближение к корню:

x0 =1.

Условие окончания процесса уточнения корня. Для оценки погрешности метода

Ньютона справедливо соотношение:

xn x

(xn

xn 1)

, где M2 – наибольшее

значение

(x)

m1 –наименьшее значение

на отрезке[a;b]. Из требования

f (x)

обеспечения

точности

следует

условие

окончания

вычислений

xn 1

2m1

2) «Ручной расчет»

трех итераций

Для получения решения уравнения методом Ньютона

воспользуемся

следующей

рекуррентной формулой: x

n 1

f(xn )

f '(xn )

В нашем случае x

n 1

1 3xn

cosxn , x0 =1.

3 sinxn

f (x) 1 3x cos(x)

f1(x) d

f (x) sin(x)

x0 1

f (x0) 1.4597

x1 x0

f(x0)

0.62

f (x1) 0.046

f1(x0)

f(x1)

x2 x1

0.607121

f(x2) 6.788 10

f1(x1)

f(x2)

x3 x2

0.607102

f(x3) 1.484 10

f1(x2)

Представим вычисления в виде следующей табл. 2-2b.

f(xk)

-1.4597

0.6200

-4.62•10-2

0.607121

-6. 788 •10-5

0.607102

-1.484 •10-10

Страница 7

Тема1.2.Методы решениянелинейных уравнений (Лабораторныйпрактикум)

3) Погрешность численного решения нелинейных уравнений

Оценим погрешность после трех итераций:

m	f (0)			3,	M	f (0)	1,	x* x		M (x		x		)2
m	f (0)			3,	M	f (0)	1,	x* x	3	2	3		2	.
1					2				3	2m1
Тогда		x* x			0.000002.					2m1
Тогда		x* x			0.000002.
			3

Метод хорд

1) Исследование задания для «ручного расчета».

Проверка выполнения условий сходимости. Для сходимости метода необходимо

знакопостоянство f (x) на отрезке [a;b].

Выбор начального приближения. Вид рекуррентной формулы зависит от того, какая из точек a или b является неподвижной. Неподвижен тот конец отрезка [a;b] , для

которого знак функции f(x) совпадает со знаком ее второй производной. Тогда второй конец отрезка можно принять за начальное приближение к корню, то есть точку х0.

Рекуррентная формула метода хорд:

		f(xn )

xn 1 xn			(x xn), где x	- неподвижная точка.


	f(x)	f(xn )

На этапе отделения корня было показано, что для функции f(x)=1–3x+cosx вторая производная f (x)<0 на отрезке [0;1] и, следовательно, неподвижной точкой является

точка x=b=1, так как f (1) f (1) 0.

Таким образом, полагая x0 =a=0, получим сходящуюся последовательность приближений

к корню.

В рассматриваемой задаче рекуррентная формула принимает следующий вид

xn 1 xn	f(xn )	(1 xn
	f(1) f(x )
	n

Условие окончания процесса уточнения корня. Оценку погрешности можно проводить

по любой из формул

x* xn

f (xn )

или

x* xn

M1 m1

xn xn 1

где m1 и M1 –

M1<m1 можно

наименьшее и наибольшее значения

на отрезке. В случае, если

(x)

использовать правило останова

xn xn 1

2) «Ручной расчет» трех итераций

Для получения решения уравнения методом хорд воспользуемся следующей рекуррентной формулой:

x	k 1	x	k	f(xk )	(1 x	k	x0 = 0.
				f(1) f(x )

				k

Тема1.2.Методы решениянелинейных уравнений (Лабораторныйпрактикум)

Страница 8

f (x) 1		3x cos (x)
i 03
x0 0
		f x		1 x
x x		0
x x		f(1) f	x
1	0	f(1) f	x	0
			0
x1 0.57809
f x 0.10325
1
		f x		1 x
x x		1
x x		f(1) f	x
2	1	f(1) f	x	1
			1
x2 0.60596
f x	4.0808 10 3
2
		f x		1 x
x x		2
x x		f(1) f	x
3	2	f(1) f	x	2
			2
x3 0.60706
f x	1.59047 10 4
3

Результаты вычислений представлены в виде следующей таблицы:

n	Xn	f(xn)
0	0	2
1	0.5781	0.1032549
2	0.6059	4.080772 •10-3
3	0.6070	1.590771•10-4

3)Погрешность численного решения нелинейного уравнения

Погрешность результата, вычисленного методом хорд, оцениваем по формуле

x* x

M1 m1

n 1

. Тогда после трех итераций

x* x

3.841 3 0.0011 3.08 10 4,

x* x

0.53 10 4.

4. Решение уравнения средствами MathCad

Для решения нелинейных уравнений вида f(x) = 0 в Mathcad используется функция root(f(x), x, a, b), где f(x) – выражение, стоящее в левой части решаемого уравнения, x – аргумент функции, a и b –границы отрезка с корнем. В приведенном ниже примере z - имя переменной, которой присваивается найденное значение корня. Функция root реализует вычисление корня уравнения численным методом с точностью TOL (по умолчанию TOL =1.10-3).

f (x) 1 3x cos(x)
z root (f (x)x 0 1) 0.6071	Страница 9
f (z) 0
Тема1.2.Методы решениянелинейных уравнений (Лабораторныйпрактикум)

2.6. Контрольные вопросы по теме

Методы решения нелинейных уравнений

1.Что представляет собой нелинейное уравнение?

2.Что является корнем нелинейного уравнения f(x)=0?

3.Чемуравна функция в точке корня?

4.Как называется процесс нахождения возможно более узкого отрезка, содержащего только один корень уравнения ?

5.Каково условие существования на отрезке [a;b] хотя бы одного корня?

6.При каких условиях корень x будет единственным на отрезке [a;b]?

7.Процесс решения нелинейного уравнения состоит из...

8.Как называются этапы решения нелинейного уравнения?

9.В чем заключается этап «отделения корней» нелинейного уравнения?

10.Что такое начальное приближение к корню?

11.Что определяется на этапе уточнения корней?

12.Какие методы не относятся к методам отделения корня?

13.Какие методы не относятся к методам уточнения корня?

14.Какие методы используются на этапе отделения корней?

15.Что необходимо, чтобы выбрать x0 в качестве начального приближения в методе Ньютона?

16.Что является необходимым условием существования корня на отрезке [a;b]?

17.Какой метод решения нелинейного уравнения требует более близкого к корню начального значения?

18.Назовите метод решения нелинейного уравнения, в результате которого получается последовательность вложенных отрезков?

19.Можно ли уточнить корень уравнения графическим методом?

20.Что является первым приближением к корню, отделенному на отрезке [a;b], при решении нелинейного уравнения методом половинного деления?

21.При каких условиях метод половинного деления всегда находит корень уравнения f(x)=0?

22.Что означает термин - «метод расходится»?

23.Какой метод решения нелинейного уравнения обладает квадратичной сходимостью?

24.Каково правило выбора итерирующей функции при использовании метода итераций?

25.Что принимается за начальное приближение в методе итерации?

26.Каково правило выбора неподвижной точки при использовании метода хорд?

27.Какое значение выбирается в качестве начального приближения в методе хорд?

28.Почему необходим этап отделения корней?

29.При каких условиях метод хорд позволяет вычислить отделенный корень с заданной погрешностью?

30.Для каких функций не рекомендуется применять метод Ньютона?

31.Что можно сказать о методе итерации, если на заданном отрезке имеются два корня?

32.Как могут осуществляться итерации приближения к корню в процессе решения уравнения методом простой итерации?

33.Какой метод решения нелинейного уравнения обладает свойством «самокоррекции»?

34.Что относится к способам улучшения сходимости метода простой итерации?

Тема1.2.Методы решениянелинейных уравнений (Лабораторныйпрактикум)

Страница 10

1 / 51 2 3 4 5 > Следующая >>>

Соседние файлы в предмете Математические пакеты

#
11.02.2023292.38 Кб6БИК19532L5.docx
#
11.02.2023289.47 Кб3БИК19532L5.xmcd
#
11.02.20231.54 Mб4ВМиППП-Лабораторные(заочн).pdf
#
11.02.2023226.77 Кб4ЛР-02 НЛУ.docx
#
11.02.2023521.16 Кб6ЛР-03 Интерполяция.docx
#
11.02.2023128.76 Кб7ЛР-04 Интегрирование.docx
#
11.02.2023154.48 Кб4ЛР-05 ОДУ.docx
#
11.02.2023132.68 Кб12ЛР-06 Одномерная оптимизация.docx