6.6.5. Технология решения задач одномерной оптимизации средствами математических пакетов

Пакет Mathcad с помощью встроенных функций решает задачу нахождения только локального экстремума. Для нахождения глобального экстремума необходимо вычислить все локальные экстремумы и выбрать среди них наибольший (наименьший). Отметим несколько подходов в поиске экстремума.

Для непрерывной функции от одной переменной можно использовать равенство нулю её производной, и путем решения полученного уравнения получить точки экстремумов. Уравнение можно решить с использованием встроенной функции root. При этом следует принимать во внимание знак второй производной. Если на отрезке, содержащем точку экстремума, , то это локальный минимум, а если , то это локальный максимум.

Пример 6.6.5-1. Найти глобальный минимум функции .

Дальнейшее исследование показало, что глобальным минимумом является точка х = -3.679.

Для непрерывных функций также удобно пользоваться такими встроенными функциями как Maximize(y,x) и Minimize(y,x). Здесь ключевое слово Given можно опускать, поскольку оно необходимо лишь при наличии ограничений.

Пример 6.6.5-2. Найти минимум и максимум функции y(x)=2x³-16x+5.

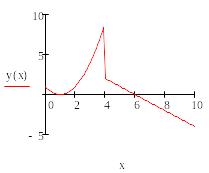
Для ступенчатой функции или функции с переломами можно использовать встроенную функцию Minеrr( ). Предварительно по графику выбирается число, заведомо большее (или меньшее) экстремального значения функции, и записывается в качестве ограничения в блоке Given. Функция Minеrr( ) возвращает значение аргумента, при котором расхождение между заданным числом и значением функции минимально.

Пример 6.6.5-3. Найти минимум и максимум ступенчатой функции.

Тема 6.7. Аппроксимация функций

6.7.1. Постановка задачи аппроксимации

6.7.2. Метод наименьших квадратов

6.7.3. Технология решения задач аппроксимации функций средствами математических пакетов

6.7.1. Постановка задачи аппроксимации

Задача аппроксимации (приближения) функции заключается в замене некоторой функции y=f(x) другой функцией g(x, a₀, a₁, ..., a_n) таким образом, чтобы отклонение g(x, a0, a1, ..., an) от f(x) удовлетворяло в некоторой области (на множестве Х) определённому условию. Если множество Х дискретно (состоит из отдельных точек), то приближение называется точечным, если же Х есть отрезок [a;b], то приближение называется интегральным.

Если функция f(x) задана таблично, то аппроксимирующая функция g(x, a₀, a₁, ..., a_n) должна удовлетворять определённому критерию соответствия ее значений табличным данным.

Подбор эмпирических формул состоит из двух этапов – выбора вида формулы и определения содержащихся в ней коэффициентов.

Если неизвестен вид аппроксимирующей зависимости, то в качестве эмпирической формулы обычно выбирают один из известных видов функций: алгебраический многочлен, показательную, логарифмическую или другую функцию в зависимости от свойств аппроксимируемой функции. Поскольку аппроксимирующая функция, полученная эмпирическим путем, в ходе последующих исследований, как правило, подвергается преобразованиям, то стараются выбирать наиболее простую формулу, удовлетворяющую требованиям точности. Часто в качестве эмпирической формулы выбирают зависимость, описываемую алгебраическим многочленом невысокого порядка.

Наиболее распространен способ выбора функции в виде многочлена:

,

где φ(x,a₀,a₁,...,a_n)=a₀φ₀(x)+a₁φ₁(x)+...+a_mφ_m(x), а

φ₀(x), φ₁(x), ..., φ_m(x) – базисные функции (m-степень аппроксимирующего полинома).

Один из возможных базисов – степенной: φ₀(x)=1, φ₁(x)=х, ..., φ_m(x)=х^m.

Обычно степень аппроксимирующего полинома m<<n, a^T=(a₀,a₁,...,a_m) – вектор коэффициентов. Если погрешность исходных данных e, то количество базисных функций выбирается так, чтобы . Здесь S – численное значение критерия близости аппроксимирующей функции φ(x, a₀, a₁, ..., a_n) и табличных данных. Отклонения между опытными данными и значениями эмпирической функции

e_i = φ(x_i, a₀, a₁, ..., a_m) – y_i, i = 0,1,2,...,n.

Методы определения коэффициентов выбранной эмпирической функции различаются критерием минимизации отклонений.