
1 семестр / Funkcii_dvuh_i_treh__peremennyh_dlja_tipovogo__vveden_ostatochnyj_chlen_dlja_sajta1
.pdf
Функции нескольких переменных.
1. Основные понятия.
Исследование функции нескольких переменных проведем на примерах функций двух и трех переменных, так как все данные определения и полученные результаты справедливы для функций n переменных.
Определение. Если в пространстве каждой точке P= |
, |
|
|
принадлежащей некоторому множеству D, ставится в соответствие |
|
||
единственное действительное значение z |
, то говорят, что на множестве D |
||
задана функция двух переменных и обозначают |
. |
|
|
Областью определения функции |
является множество |
. |
|
Графиком функции двух переменных |
будет поверхность в . |
|
|
Например, графиком функции |
|
будет |
|
эллиптический параболоид (рис.1) |
|
|
|
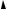 z
z
, |
= |
2 |
+ |
2 |
|
|
D |
3 |
y |
|
|
3
Рис. 1.
x
Определение. Функция трех переменных каждой точке |
, |
||
принадлежащей некоторому множеству D, ставит в соответствие единственное |
|||
действительное значение u |
, её обозначают |
|
|
, |
или |
, |
|
|
1 |
|
|
Областью определения функции трех переменных u=f(x,y,z) является множество трехмерного пространства . График функции лежит в четырёхмерном пространстве, представить его затруднительно.
В пространстве расстояние между двумя точками
|
|
определяется следующим образом |
||
|
|
|
|
|
√ |
. |
|
||
В пространстве расстояние между двумя точками |
||||
|
|
определяет функция |
||
|
|
|
||
√ |
. |
|||
Определение. |
|
- окрестностью точки |
трехмерного |
|||
пространства |
называется множество точек |
таких, что |
и |
|||
обозначается |
|
. |
|
|
|
|
Определение. |
Проколотой |
- окрестностью точки |
|
|
||
трехмерного пространства |
называется множество точек |
таких, что |
||||
|
и обозначается ̇ |
. |
|
|
||
Определение. |
Число А называется пределом функции |
) при |
||||
стремлении точки |
, если для |
|
|
|
||
или |
̇ |
Как видим, понятие предела для функции многих переменных такое же, как и для функции одной переменной.
Но существует и небольшое отличие:
Если в (на прямой) мы можем стремится к точке двумя способами, слева
и справа, то в |
( на плоскости) и в |
( в пространстве) способов стремится к |
точке становится бесконечно много. |
|
|
Для существования предела мы должны показать, что получаемый результат( предел) не зависит от способа подхода к предельной точке. Если при различных подходах к предельной точке получаем разные значения предела
2

функции, то это является доказательством того, что предел функции не существует.
Иногда встречаются задачи, в которых необходимо вычислить предел функции двух( или трех) переменных только по одной заданной линии подхода к предельной точке. И если не существует общего предела, то предел по какомунибудь частному направлению может существовать.
Рассмотрим функцию |
|
и попробуем найти предел при |
|
стремлении к началу координат, к точке
( |
|
) |
|
||
Вывод: предела данной функции при стремление к точке |
не |
|
существует. |
|
|
Такой же вывод могли получить, если бы перешли к полярным координатам, тогда
вместо стремления двух переменных |
у нас будет одно стремление |
И видно, что предел завит от угла, от пути подхода к предельной точке |
. |
||
Рассмотрим функцию |
|
и попробуем найти предел при |
|
|
|
||
стремлении к началу координат, к точке |
. |
|
|
Перейдем к полярным координатам |
|
|
|
|
|
3 |
|

| |
Предел существует и не меняет значения при произвольном способе подхода к
предельной точке |
. |
2. Непрерывность функций нескольких переменных.
Определение. |
Функция u= f( |
называется непрерывной |
в точке , если |
|
|
1.функция u= |
определена в точке |
, |
2.существует конечный предела при
3.предел существует и равен значению функции в точке
Определение. Функция u= f( |
называется непрерывной на области |
||
D, если она непрерывна в каждой точке области D. |
|||
Если не выполняется хотя бы одно условие из определения |
|||
непрерывности функции в точке |
, то такая точка называется точкой |
||
разрыва функции u= |
. |
|
|
Например, если: |
|
|
|
1.функция u= |
не определена в точке , |
||
2.Не существует конечного предела при
3.предел существует, но не равен значению функции в точке
4

Функция трех ( двух )переменных может иметь множество точек разрыва, образующих например, одну, две линии разрыва или даже произвольное множество.
Пример 1. |
|
|
|
|
|
|
а) функция |
|
|
имеет линию разрыва |
|||
|
|
|||||
б) функция |
|
|
|
|
имеет две линии разрыва, |
|
|
|
|
||||
в) если функцию |
|
|
|
|
|
доопределить следующим образом |
|
|
|
|
|
||
{
то останется только одна линия разрыва |
. |
Таким образом, функции многих переменных предполагают огромное разнообразие различных задач.
ВЫУЧИТЬ!!!
3. Дифференцирование функций нескольких переменных.
Определение. Частным приращением функции |
по переменной |
называется приращение |
|
Определение. Частной производной первого порядка функции
по одной из независимый переменный |
называется предел |
||||||
|
|
|
|
|
|
|
|
частного приращения функции |
по этой переменной к |
||||||
приращению переменной, когда приращение переменной стремится к 0. |
|||||||
( |
) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частную производную первого порядка функции
5

по переменный обозначают: |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
Функция трех переменных |
|
|
|
|
имеет три частные производные |
|||||
первого порядка, |
|
|
|
|
|
|
|
|||
по x |
|
|
|
|
|
|
|
|||
|
|
|
|
( |
) |
|||||
|
|
|
|
|
|
|
|
|
|
|
по y
( |
) |
|
|
по z
( |
) |
|
|
Функция двух переменных |
|
имеет две частные производные |
||||
первого порядка, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение. Приращение |
называется |
частным приращением данной функции по переменной |
. Приращение |
называется частным приращением данной
функции по переменной .
Из определения частной производной первого порядка функции
видно, что при дифференцировании функции нескольких переменных по одной из них, все остальные переменные следует считать
6

постоянными и, следовательно, можно пользоваться известными правилами и формулами дифференцирования функции одной переменной.
Пример 2.
a) Найти все частные производные первого порядка функции двух переменных
√
Решение: При вычислении частной производной по переменной переменную считаем константой
√ √
при вычислении частной производной по переменной переменную считаем константой
√
б) Вычислить все частные производные первого порядка функции трех переменных
Решение: Аналогично предыдущему примеру из пункта а), при вычислении частной производной по переменной , переменные и считаем константами.
Частная производная вычисляется при фиксированных и z , т.е.
и
Частная производная |
|
берется при фиксированных и , т.е. |
и |
|
7

Геометрический смысл частных производных для функций двух переменных.
Если через Р( |
проведем плоскостью |
|
|
( плоскость |
||||
параллельную плоскости XOZ), то она пересечёт поверхность, |
||||||||
соответствующую функции |
, по некоторой кривой |
|||||||
. |
Производная |
|
, найденная в точке |
Р( |
|
, будет равна тангенсу |
||
|
||||||||
угла ( |
наклона касательной, к кривой |
в точке Р( |
||||||
|
вому коэффициенту (k) касательной, т.е. |
|
tg( =k. (Рис. 2) |
|||||
|
|
|||||||
z=f(x,y) |
Z |
Z |
z=f(x,y) |
|
z=f(x,y=const) |
||||
|
|
|
||
|
|
z=f(x=const,y) |
|
|
Y |
Y |
|
y=const |
β |
|
α |
|
|
x=const |
|
X |
Рис. 2 |
Рис. 3 |
|
X |
|
|
|
Если через Р( |
построить плоскостью |
|
|
( плоскость |
|||
параллельную плоскости YOZ), то она пересечёт поверхность, |
|||||||
соответствующую функции z f x, y , по некоторой кривой |
|||||||
. |
Производная |
|
, найденная в точке |
Р( |
|
, будет равна тангенсу |
|
|
|||||||
угла ( |
наклона касательной, к кривой |
в точке Р( |
|||||
вому коэффициенту (k) касательной, т.е. |
|
tg( =k. (Рис. 3) |
|||||
|
|||||||
Предположим, что функция нескольких переменных имеет частные производные первого порядка во всех точках области определения D. Эти производные являются функциями нескольких переменных в области D и они тоже могут иметь частные производные первого порядка.
Определение. Частные производные первого порядка от частных производных первого порядка функции нескольких
8

переменных называются частными производными второго порядка функции нескольких переменных и обозначаются
( ) или ( ) .
Аналогично определяются частные производные более высокого порядка.
Определение. Частная производная высшего порядка, взятая по разным
переменным, называется смешанной производной и обозначается |
|
|
( |
|
) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(частная производная второго порядка) или |
|
|
|
( |
|
( |
|
)) |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
( |
|
|
|
|
|
( |
|
|
|
|
)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(частные производные третьего порядка) |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Например, функция двух переменных |
|
|
|
|
|
|
|
|
|
имеет четыре частные |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
производные второго порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; транскрипция «дэ два эф по дэ икс в квадрате» |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; транскрипция «дэ два эф по дэ икс по дэ игрек» |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; транскрипция «дэ два эф по дэ игрек по дэ икс » |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; транскрипция «дэ два эф по дэ игрек в квадрате» |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
а функция трех переменных |
имеет уже девять частных |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
производных второго порядка. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
( |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
( |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
( |
|
|
) |
|
|
|
|
|
|
|
|
( |
|
|
) |
|
|
|
|
|
|
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вобщем случае, смешанные производные не равны друг другу, например
,поэтому порядок написания переменной в знаменателе частной производной имеет важное значение.
9

Имеет место теорема о равенстве смешанных производных. ВЫУЧИТЬ!!!
Теорема. 1. Если функция |
определена и непрерывна в |
окрестности точки Р |
вместе со своими частными производными до k- |
ого порядка включительно, то смешанные производные функции до k-ого порядка включительно в этой точке, не зависят от порядка дифференцирования.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
) |
|
|
( |
|
|
) |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
( |
|
( |
|
)) |
|
|
( |
|
|
( |
|
|
)) |
|
|
( |
|
|
( |
|
)) |
|
( |
|
( |
|
)) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Например, если функция |
|
|
|
|
|
|
|
|
|
|
непрерывна вместе со своими частными |
|||||||||||||||||||||||||
производными до второго порядка включительно в окрестности точки |
||||||||||||||||||||||||||||||||||||
( |
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Для функции двух переменных |
|
|
|
|
непрерывной вместе со своими |
|||||||||||||||||||||||||||||||
частными производными до третьего порядка включительно в окрестности точки (
.
Пример 3.
а) Найти смешанные производные второго порядка функции
и проверить их равенство.
Решение: Функция является непрерывной по переменным x и y. Найдем вторые смешанные производные
( )
( |
|
) |
|
( |
|
) |
|
|
|
то есть производные |
|
|
|
. |
|
|
10
