8945

71

4.2.4. Логические выражения и таблицы истинности

Каждое составное высказывание можно выразить в виде формулы

(логического выражения), в которую входят логические переменные,

обозначающие высказывания, и знаки логических операций, обозначаю-

щие логические функции.

Для записи составного высказывания в виде логического выраж е-

ния на формальном языке (языке алгебры логики) в составном высказ ы-

вании нужно выделить простые высказывания и логические связи между

ними.

Запишем в форме логического выражения составное высказывание

Тогда составное высказывание можно записать в следующей фор-

ме:

« ( A или B) и ( A или B ) ».

Теперь необходимо записать высказывание в форме логического выражения с учетом последовательности выполнения логических опер а-

ций. При выполнении логических операций определен следующий пор я-

док их выполнения: инверсия, конъюнкция, дизъюнкция. Для изменения указанного порядка могут использоваться скобки:

F ( A B) & ( A B ).

Истинность или ложность составных высказываний можно опред е-

лять чисто формально, руководствуясь законами алгебры высказ ываний,

не обращаясь к смысловому содержанию высказываний.

Подставим в логическое выражение значения логических перемен-

ных и, используя таблицы истинности базовых логических операций,

получим значение логической функции:

72

F ( A B) & ( A B ) (0 1) & (1 0) 1 &1 1

Для каждого составного высказывания (логического выражения)

можно построить таблицу истинности, которая определяет его исти н-

ность или ложность при всех возможных комбинациях исходных знач е-

ний простых высказываний (логических переменных).

При построении таблиц истинности целесообразно руководство-

ваться определенной последовательностью действий.

Во–первых, необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений л о-

гических переменных, входящих в логическое выражение. Ес ли количе-

строк в таблице истинности должно быть равно 4.

Во–вторых, необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс к о-

личество логических операций.

Функция F ( A B) & ( A B ) содержит две переменные и пять ло-

гических операций, то есть количество столбцов таблицы истинности равно семи.

В–третьих, необходимо построить таблицу истинности с указа н-

ным количеством строк и столбцов, обозначить столбцы и внести в та б-

лицу возможные наборы значений исходных логических переме нных.

В–четвертых, необходимо заполнить таблицу истинности по столб-

цам, выполняя базовые логические операции в необходимой последов а-

тельности и в соответствии с их таблицами истинности (табл. 4.4). Те-

перь мы можем определить значение логической функции для любого набора значений логических переменных.

Равносильные логические выражения. Логические выражения, у

которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений

Теперь построим таблицу истинности логического выражения

A B (табл. 4.6).

Значения в последних столбцах таблиц истинности совпадают, сле-

довательно, логические выражения равносильны:

A & B = A B

74

Таблица 4.6. Таблица истинности логического выражения A B

4.2.4.1.Задания

1.Записать составное высказывание

« (2 2 4 и 3 3 9) или (2 2 4 и 3 3 9) » в форме логического выра-

жения. Построить таблицу истинности.

2. Доказать, используя таблицы истинности, что логические выр а-

жения A B и A & B равносильны.

4.2.5. Логические функции

Любое составное высказывание можно рассматривать как логич е-

скую функцию F(X1, X2, …, Xn), аргументами которой являются логиче-

ские переменные X1, X2, …, Xn (простые высказывания). Сама функция и аргументы могут принимать только два различных значения: «истина»

(1) и «ложь» (0).

Выше были рассмотрены функции двух аргументов: логическое умножение F(A,B) = А & В, логическое сложение F(A,B) = A B, а также логическое отрицание F(A) = A , в котором значение второго аргумента можно считать равным нулю.

Каждая логическая функция двух аргументов имеет четыре во з-

можных набора значений аргументов. По формуле ( 4.1) мы можем опре-

делить, какое количество различных логических функций двух аргуме н-

тов может существовать:

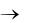
75

N = 24 = 16.

Таким образом, существует 16 различных логических функций двух аргументов, каждая из которых задается своей таблицей истинн о-

сти (табл. 4.7).

Таблица 4.7. Таблицы истинности логических функций двух аргу-

ментов

Легко заметить, что здесь логическая функция F2 является функци-

ей логического умножения, F8 — функцией логического сложения, F13 —

функцией логического отрицания для аргумента А и F11 — функцией ло-

гического отрицания для аргумента В.

Логическое следование (импликация). Логическое следо вание (им-

пликация) образуется соединением двух высказываний в одно с пом о-

щью оборота речи «если..., то...».

Логическая операция импликации «если А, то В», обозначается

A B и выражается с помощью логической функции F14, которая задает-

ся соответствующей таблицей истинности (табл. 4.8).

Составное высказывание, образованное с помощью операции л о-

гического следования (импликации), ложно тогда и только тогда, к о-

гда из истинной предпосылки (первого высказывания) следует ло ж-

ный вывод (второе высказывание).

76

Таблица 4.8. Таблица истинности логической функции «имплика-

ция»

Например, высказывание «Если число делится на 10, то оно дели т-

ся на 5» истинно, так как истинны и первое высказывание (пред посыл-

ка), и второе высказывание (вывод). Высказывание «Если число делится на 10, то оно делится на 3» ложно, так как из истинной предпосылки д е-

лается ложный вывод. Однако операция логического следования не-

сколько отличается от обычного понимания слова «сле дует». Если пер-

вое высказывание (предпосылка) ложно, то вне зависимости от истинн о-

сти или ложности второго высказывания (вывода) составное высказыв а-

ние истинно. Это можно понимать таким образом, что из неверной пре д-

посылки может следовать что угодно. В алгебре высказываний все логи-

ческие функции могут быть сведены путем логических преобразований к трем базовым: логическому умножению, логическому сложению и лог и-

77

Таблицы истинности совпадают, что и требовалось доказать.

Логическое равенство (эквивалентность). Логическое равенство

(эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «... тогда и только тогда, когда ...».

Логическая операция эквивалентности «А тогда и только тогда, ко-

гда В» обозначается А~В и выражается с помощью логической функции

F10, которая задается соответствующей таблицей истинности (табл.

4.10).

Таблица 4.10. Таблица истинности логической функции эквива-

лентности

Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.

Рассмотрим, например, два высказывания: А = «Компьютер может производить вычисления» и В = «Компьютер включен». Составное вы-

сказывание, полученное с помощью операции эквивалентности, истинно,

когда оба высказывания либо истинны, либо ложны:

«Компьютер может производить вычисления то гда и только тогда,

когда компьютер включен».

«Компьютер не может производить вычисления тогда и только т о-

гда, когда компьютер не включен».

Составное высказывание, полученное с помощью операции эквив а-

лентности, ложно, когда одно высказывание истинно, а другое — ложно:

78

«Компьютер может производить вычисления тогда и только тогда,

когда компьютер не включен».

«Компьютер не может производить вычисления тогда и только т о-

гда, когда компьютер включен».

4.2.5.1.Вопросы и задания.

1.Какое количество логических функций двух аргументов сущест-

вует и почему?

2. Какие логические функции двух аргументов имеют свои назв а-

ния?

3. Доказать, используя таблицы истинности, что операция эквив а-

лентности А ~ В равносильна логическому выражению: ( A B ) & ( A B) .

4.3. Логические законы и правила преобразования логических выражений

Законы логики отражают наиболее важные закономерности логич е-

ского мышления. В алгебре высказываний законы логики записыв аются в виде формул, которые позволяют проводить эквивалентные преобраз о-

вания логических выражений.

Закон тождества. Всякое высказывание тождественно самому се-

бе: A = A.

Закон непротиворечия. Высказывание не может быть одновремен-

но истинным и ложным. Если высказывание А истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение вы-

сказывания и его отрицания должно быть ложно: A & A 0

Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение «истина»: A A 1

79

Закон двойного отрицания. Если дважды отрицать некоторое вы-

сказывание, то в результате мы получим исходное высказывание: A A

Законы де Моргана.

A B A & B

A & B A B

Для выполнения преобразований логических выражений важное значение имеют законы алгебраических преобразований. Многие из них имеют аналоги в обычной алгебре.

Закон коммутативности. В обычной алгебре слагаемые и множи-

тели можно менять местами. В алгебре выска зываний можно менять местами логические переменные при операциях логического умножения и логического сложения:

Закон ассоциативности. Если в логическом выражении исполь-

зуются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвол ь-

но их расставлять:

Закон дистрибутивности. В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказыв а-

ний можно выносить за скобки как общие множители, так и общие сл а-

гаемые:

Рассмотрим в качестве примера применения законов логики прео б-

разование логического выражения. Пусть нам необходимо упростить л о-

гическое выражение:

(А & В) 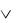(А & B ).

Воспользуемся законом дистрибутивности и вынесем за скобки А:

4.4. Решение логических задач

Логические задачи обычно формулируются на естественном языке.

В первую очередь их необходимо формализовать, то есть записать на языке алгебры высказываний. Полученные логические выражения нео б-

ходимо упростить и проанализировать. Для этого иногда бывает необхо-

димо построить таблицу истинности полученного логического выраж е-

ния.

Пример 1. Преобразование логических выражений.

Условие задачи. В школе-новостройке в каждой из двух аудиторий