Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

8316

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.27 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

ВАРИАНТ 1

	0,			x 0;
1.	x	2			2.
	F (x)		,	x (0; 8];

	64			x 8
	1,

3. X ~ N(1 ; 4 )

ВАРИАНТ 2

F (x) x 2

1. ,

1001,

3.	X ~ N( 2 ; 6 )
ВАРИАНТ 3
		0,
	F (x)	x	2
1.				,

		16
		1,

3.	X ~ N(3 ; 2 )

а) 0<X<4; б)

x 0;

x (0; 10];

x 10

а) 3<X<7; б)

x 0;

x (0; 4];

x 4

а) 1<X<5; б)

Продолжение ПРИЛОЖЕНИЯ Г

f ( x) a cos	2			;
f ( x) a cos		x		;
			2		2

X>5; в) Y = 3X – 1

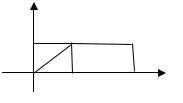
f(x

2.a

0	1	2	х

X<1; в) Y = -2-3X

f(x

2.a

0	2	4	х

X 4 в) Y = 3-X

							Продолжение ПРИЛОЖЕНИЯ Г
ВАРИАНТ 4
		0,2			x 0;					f(x)
	F (x)	x
1.				,	x (0; 9];	2.		a
1.				,	x (0; 9];	2.		a
		81			x 9
		1,			x 9

								0			1			3		х
	X ~ N( 2 ; 1 )

3.					а) 0<X<3;	б) X<1			в)	Y = 3X+1
ВАРИАНТ 5
		0,			x 0;
	F (x)	x	2				f (x) a x2					1	, x 0;				2
1.				,	x (0; 3];	2.
1.				,	x (0; 3];	2.						3
		9										3
		9			x 3
		1,			x 3

3.	X ~ N( 2 ; 3 ) а) 0<X<2;					б) X -1				в) Y = 3X +2
ВАРИАНТ 6
		0,			x 0;
	F (x)	x	2
1.				,	x (0; 7];	2.	f ( x) a sin x,						x		0;
1.				,	x (0; 7];	2.	f ( x) a sin x,						x		0;
		49														2
		1,			x 7

3.	X ~ N( 2 ;		4 )		а) 0<X<2;	б) X>1			в)		Y = 3-2X

Продолжение ПРИЛОЖЕНИЯ Г

ВАРИАНТ 7

	2
0,			x 0;
1. F(x) x		,	x (0; 1];	2.
1,			x 1

f ( x) a x2		1	,		x 1; 2
f ( x) a x2			,		x 1; 2
	3
3.	X ~ N( 0,5 ;						2 )	а) 0 X 1;
ВАРИАНТ 8
				0,			x 0;
	F (x)			x	2
1.						,	x (0; 6];
1.						,	x (0; 6];
				36			x 6
				1,			x 6

3.	X ~ N ( 0,5 ;						1 )	а) -1<X<0,5;
ВАРИАНТ 9
				0,			x 0;
	F (x)			x	2
1.						,	x (0; 2];
1.						,	x (0; 2];
				4			x 2
				1,			x 2

б) X<0 в) Y = 2X-2

2.
2.	f ( x) a sin 3x 0;
		6

б) X 05; в) Y = 2X – 1,5

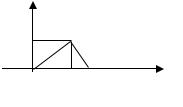
f(x)

2.a

0	2	3	х

3. X ~ N( 0,5 ; 0,4 ) а) 0,5<X<1,5; б) X<0 в) Y = 3X-1,5

Продолжение ПРИЛОЖЕНИЯ Г

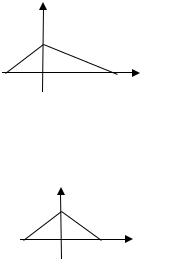
ВАРИАНТ 10

x 0;

2. f ( x) a cos x,

x 3;

F (x)

x (0; 5];

x 5

X ~ N (2 ;

4 )

а) -1<X<3,5;

б) X 3;

в) Y = 3-3X

ВАРИАНТ 11

x 0;

f(x)

1. F(x) ln(x 1),

x (0; e 1];

x e 1

-2

X ~ N( 2 ; 3 )

а) 0<X<2;

б) X>3;

в)

Y = 2X-3

ВАРИАНТ 12

x 2;

f(x)

1. F(x) 0,5(x 2),

x (2; 4];

x 4

-a

X ~ N(3 ; 4 )

а) 1<X<4;

б) X>5;

в)

Y = 0,5X-23

Продолжение ПРИЛОЖЕНИЯ Г

ВАРИАНТ 13

x 4;

1. F(x) 0,8х 3,2,

x (4; 5,25];

x 5,25

f ( x) a sin х,

x 0;

X ~ N(1 ;

2 )

а) 0<X<2;

б)

X<0;

в)

Y = 0,5X – 1

ВАРИАНТ 14

x 0;

f(x)

F (x) x

x (0; 1];

x 1

-1

X ~ N( 2 ; 4 )

а) 0<X<2;

б)

X>3;

в)

Y = 0,5X-2

ВАРИАНТ 15

x 1;

f(x)

x ( 1; 1];

1. F(x) 2

1/3

x 1

X ~ N( 1 ; 2 )

а) -1 X 1;

б)

X>0

в)

Y = 2X+3

Продолжение ПРИЛОЖЕНИЯ Г

ВАРИАНТ 16


0,	x 0;
						x 2;3
1. F (x) sin x,	x (0;		2	];	2. f (x) a x,	x 2;3
			2
	x
1,	x
		2

3.	X ~ N(0 ;			4 ) а) -2<X<0;			б)	X>1;		в)	Y = 0,5Х+ 1
ВАРИАНТ 17
	0,			x 0;									f(x)
	x2												f(x)
	x2									a
1. F (x)			,	x (0; 1,5];			2.			a
1. F (x)			,	x (0; 1,5];			2.
		2,25
	1,			x 1,5
	1,									0			2	5	х
										0			2	5	х
	X ~ N( 0,5 ; 1,5 )

3.						а) 0,5<X<1,5;		б)	X<-1			в) Y = 2Х-1
3.						а) 0,5<X<1,5;		б)	X<-1			в) Y = 2Х-1
ВАРИАНТ 18
		0,			x 1;								f(x)
		x		1
1.	F (x)				,	x (1; 3);				a
1.	F (x)			2	,	x (1; 3);				a
				2	x	3
		1,			x	3

2.
2.		0		1	4	х
		0		1	4	х

	3. X ~ N ( 2 ; 2 ) а) -2<X<0; б) X<-1 в)		Y = 1-0,5Х
	3. X ~ N ( 2 ; 2 ) а) -2<X<0; б) X<-1 в)		Y = 1-0,5Х

Продолжение ПРИЛОЖЕНИЯ Г

ВАРИАНТ 19

x 0;

х2

x 0;

1. F(x)

x (0; 2];

2. f ( x) a x

2х,

1,4

x 2

3. X ~ N(3 ;

2 )

а) 0<X<3;

б)

X 4;

в) Y = 2X – 3

ВАРИАНТ 20

x 0,2;

f(x

F(x) 0,2(5х 1),

x (0,2; 1,2);

x 1,2

X ~ N( 2 ; 1 )

а) -2<X<1;

б)

X>-1

в) Y = 3-0,5Х

ПРИЛОЖЕНИЕ Д

Варианты задания «Системы случайных величин»

Задача 1. Дана таблица распределения двумерной дискретной случайной величины (X, Y).

1.1. Найдите законы распределения случайных величин X и Y. Являются ли эти случайные величины независимыми?

1.2. Найдите ковариацию случайных величин X и Y (используйте
вычислительную формулу). Являются ли X и Y некоррелированными?
Задача 2. Дана плотность распределения f x, y системы X ,Y двух
непрерывных случайных величин в треугольнике АВС.
2.1. Найдите константу с. Найдите fX x ,	fY y - плотности

распределения случайных величин Х и Y. Выясните, зависимы или нет случайные величины Х и Y. Сформулируйте критерий независимости системы непрерывных случайных величин.

2.2. Найдите условную плотность распределения

уравнение регрессии случайной величины Y на Х. регрессии в треугольнике АВС.

Задача 1

f ( y x) и запишите Постройте линию

ВАРИАНТ		1

Х		Y
	-1	0	1
1	0,2	0,1	0,3
2	0	0,1	0,2
3	0	0,1	0

ВАРИАНТ		2

Х		Y
	1	2	3
1	0	0,1	0,1
2	0,2	0	0,2
3	0,2	0,2	0

Продолжение ПРИЛОЖЕНИЯ Д

ВАРИАНТ				3
Х				Y
	-2			-1	0
0	0,1			0,2	0,1
1	0,1			0	0,1
2	0,2			0,1	0,1
ВАРИАНТ				5
Х				Y
	-2			2	3
0	0,1			0,1	0,2
1	0,2			0	0,1
2	0,2			0,1	0
ВАРИАНТ				7
Х				Y
		-2		0	1
1		0,1		0,1	0,2
2		0,1		0,2	0,1
4		0		0,1	0,1
ВАРИАНТ				9
Х				Y
			2	3	4
-2			0,1	0	0
-1			0,2	0,3	0,1
0			0,1	0,1	0,1
ВАРИАНТ				11
Х				Y
			1	2	3
-1			0,1	0,1	0
0			0,2	0,2	0,1
1			0,2	0,1	0

ВАРИАНТ		4
Х		Y
	0	1	2
-2	0,2	0,1	0,2
-1	0,1	0,1	0
0	0,1	0,1	0,1
ВАРИАНТ		6
Х		Y
	1	2	4
-2	0	0,2	0
-1	0,2	0,1	0
0	0,2	0,2	0,1
ВАРИАНТ		8
Х		Y
	1	0	2
2	0,1	0,1	0,1
4	0,1	0,2	0
6	0,1	0,3	0
ВАРИАНТ		10
Х		Y
	-3	-2	-1
-3	0	0,1	0,2
-2	0,1	0	0,1
-1	0,2	0,1	0,2
ВАРИАНТ		12
Х		Y
	2	3	4
-1	0,1	0,1	0,1
0	0,2	0,2	0,2
1	0,1	0	0

Продолжение ПРИЛОЖЕНИЯ Д

ВАРИАНТ		13
Х		Y
	-3	0	1
-1	0	0,1	0,2
1	0,1	0,2	0,1
2	0,1	0,1	0,1
ВАРИАНТ		15
Х		Y
	0	2	3
-2	0,1	0,1	0
1	0,2	0,2	0,1
0	0,1	0,1	0,1
ВАРИАНТ		17
Х		Y
	-3	2	4
-1	0,1	0,1	0,1
0	0,1	0,2	0
1	0,2	0,2	0
ВАРИАНТ		19
Х		Y
	-1	0	2
-1	0,1	0,1	0,1
0	0,1	0,2	0,1
2	0,1	0,1	0,1

ВАРИАНТ		14
Х		Y
	-3	-2	0
1	0,1	0,2	0,2
2	0,1	0,1	0,1
3	0	0	0,2
ВАРИАНТ		16
Х		Y
	-3	0	2
1	0,1	0,2	0,1
2	0,1	0,2	0,1
3	0	0,1	0,1
ВАРИАНТ		18
Х		Y
	0	3	4
-2	0,2	0,1	0
-1	0,2	0,1	0,1
0	0,1	0,1	0,1
ВАРИАНТ		20
Х		Y
	0	2	4
1	0,2	0,1	0,1
2	0,1	0,2	0,1
3	0,1	0,1	0

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023243.49 Кб08224.pdf
#
05.02.20231.9 Mб568241.pdf
#
05.02.2023981.17 Кб18242.pdf
#
05.02.20231.12 Mб08261.pdf
#
05.02.20231.52 Mб28265.pdf
#
05.02.20231.27 Mб98316.pdf
#
13.02.20211.72 Mб3832.pdf
#
05.02.20231.44 Mб08322.pdf
#
13.02.20211.42 Mб1835.pdf
#
05.02.2023263.63 Кб08358.pdf
#
13.02.20211.34 Mб0836.pdf