Оператор for предназначен для выполнения заданного числа повторяющихся действий. Самое простое использование оператора for осуществляется следующим образом:

for count = start:step:final %count-переменная цикла, %start-ее начальное значение %final-конечное значение

%step-шаг, на который увеличивается count при каждом %следующем заходе цикла %тело цикла

end

1.1.2Порядок выполнения работы

1.Запустить Octave, создать и сохранить новый m-файл.

2.В созданном m-файле создать переменные: a, b, d, z, присвоив им случайные значения в диапазоне от 1 до 100.

3.Выполнить следующие арифметические операции и сохранить их результат в новые переменные:

a + dbz ,

a3 + bd (d b + d a ),

z+ π a b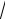d z .

4.Создать вектор-строки x = [1 1.1 1.2] и y = [1 2 3]. Транспонировать их. Найти сумму векторов x и y, разность, скалярное произведение, линейную комбинацию с коэффициентами 2 и 4 соответственно. Полученные результаты свести в таблицу.

5.Увеличить число элементов вектора x до пяти. Присвоить четвертому элементу вектора x разность первого и второго элемента вектора y, пятому элементу присвоить максимальное значение, содержащееся в векторе x.

15