7005

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

(1,0,0), (1,1,1).

Это плоскость z y . Тогда интеграл получается

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

2.15 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 158 9 10 11 12 13 14 15 > Следующая >>>

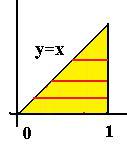
1	1			3		1

6x 2 3x 2 4x 2 x2	dx = 6x 2 dx =	6	x			= 2.

0	0	3				0

Ответ. 2.
					1		x
Задача 5. Сменить порядок интегрирования dx f (x, y)dy .
					0		0
Решение. Сначала построим чертѐж.		При каждом x переменная y

растѐт от 0 до x , то есть точки образуют треугольник. А теперь проведѐм не вертикальные, а горизонтальные линии.

Линия y x , задающая верхнюю границу, для левой границы может быть переписана как x y . Горизонтальный отрезок начинается с этой наклонной линии и завершается при x 1. Таким образом,

1 1

Ответ. dy f (x, y)dx .

0 y

Домашняя задача. Вычислить интеграл xydxdy , где D область,

ограниченная линиями y 0 , x 1, y x 2 . Ответ. 1/12.

ПРАКТИКА № 11.

1	3	x
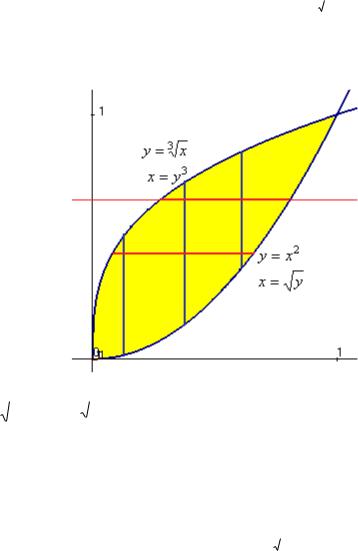
Задача 1. Изменить порядок интегрирования: dx f (x, y)dy .
0	x2

Решение. Сделаем чертѐж, также выразим в каждом уравнении через обратную функцию.

Уравнение y x 2 с помощью обратной функции будет задано в виде

				соответственно x y3 .
x	y , а y 3 x			соответственно x y3 .

Нижняя граница здесь становится правой, а верхняя граница исполняет роль левой. Ведь если мы проводим вертикальные отрезки внутри фигуры, они начинаются от квадратичной параболы, то есть при движении снизу вверх точка начинает двигаться от этой линии. А по горизонтальным, наоборот, точка при движении слева направо движется до этой линии, а не от неѐ (см. красные линии). Тогда после

1		y
смены порядка, интеграл будет в виде: dy f (x, y)dx .
0	y2

1		y
Ответ. dy f (x, y)dx .
0	y2

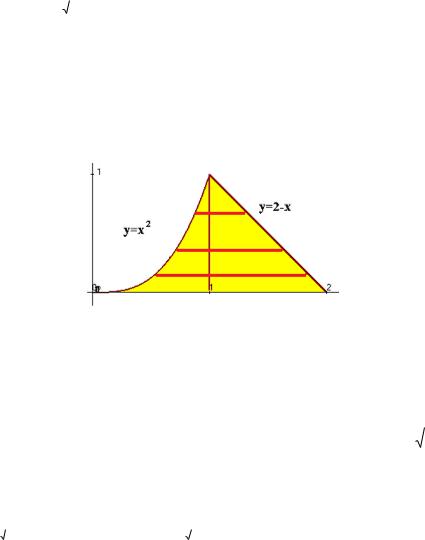
Задача 2. Сменить порядок интегрирования в двойном интеграле:

1	x2	2	2 x
dx		f (x, y)dy dx f (x, y)dy .
0	0	1	0

Решение. Построим чертѐж.

Видно, что здесь верхняя граница переходит с одной кривой на другую, поэтому от 0 до 1 и от 1 до 2 пришлось разбить на 2 разных слагаемых, если внешняя переменная x . А если внешняя переменная будет y , то надо будет найти левую и правую границы горизонтальных отрезков. А они не переходят на другую кривую:

левая всегда на параболе, а правая граница на линии

y 2 x . Если

y x 2 будет

записать через обратные функции, то вместо

y , а

вместо

y 2 x

соответственно,

x 2 y . Тогда вся область будет

учтена

сразу,

то есть

два

слагаемых

свернутся

одно:

2 y

dy f (x, y)dx .

Ответ. dy f (x, y)dx .

x 2

Задача 3. Изменить порядок интегрирования:

dx fdy dx fdy .

Решение. Построим чертѐж.

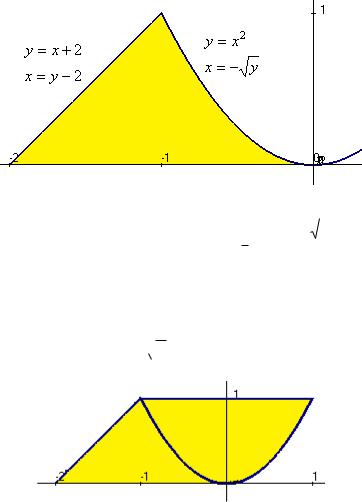
Перепишем через обратные функции. Уравнение y x 2

	y x 2
записывается в виде x y 2 , а	y x 2	в виде x y .

1 y

Тогда получим такой ответ. Ответ. dy f dx .

0 y 2

Замечание. Перед корнем квадратным именно минус, потому что x 0, то есть именно отрицательная ветвь корня. Если по ошибке не

заметить этого и взять x 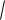y , то получится продление до правой ветви, и совсем другая область, а именно:

Тройной интеграл в декартовых координатах.

Задача 4.	Вычислить (x yz)dxdydz			по кубу x, y, z [0,1] .
			D
	1	1	1
Решение.	dx dy (x yz)dz . Здесь уже 3 а не 2 вложенных цикла.
	0	0	0

1	1	1
			(x
Это также можно записать в виде:			(x
0	0		0

Сначала вычислим внутренний интеграл по Ньютона-Лейбница именно к переменной вычислении остаются в роли параметров, подставляется.

yz)dz dy dx .

z и применим формулу z , остальные при этом вместо них ничего не

1 1												2	1									1		1					y
1 1												2	1									1		1
			1								z
xz			0			y					2				dy		dx =							x						dy dx .
xz			0												dy		dx =							x						dy dx .
																						0							2
0 0													0											0
0 0													0											0
Теперь первообразная по y и формула Ньютона-Лейбница
применяется в этой скобке именно к y .
1					y			2		1					1							1
1								2		1					1
	1
	1
xy	0										dx				= x								dx . А теперь уже обычный определѐнный
xy	0										dx				= x								dx . А теперь уже обычный определѐнный
0							4			0					0							4					1
							4															4

								1						1					x2						x			1 1 3
							x
интеграл.							x									dx =												=						.
								0						4							2 4						0	2 4 4
Ответ.				3		.
Ответ.						.
		4
																																1			x		xy
Задача 5. Вычислить тройной интеграл																																dx dy (x3 y3 z)dz .
																																0			0		0
									1			x				xy										1			x		3	y	3	z	2	xy		1	x	x	5	y	5
									1			x				xy										1			x		3		3		2	xy		1	x		5		5
									dx dy (x									3		3										x								= dx
Решение.																			y		z)dz = dx																dy							dy	=
Решение.																			y		z)dz = dx											2					dy				2			dy	=
									0			0			0											0			0			2				0		0	0		2
																										0			0							0		0	0

1		5	y	6		x			1	x	11				x	12	1		1
1		5		6		x			1		11					12	1
	x						dx =					dx	=					=		.

	12									12				144					144
	12									12				144					144
0						0			0								0
0						0			0								0
Ответ.						1		.
Ответ.					144			.
					144

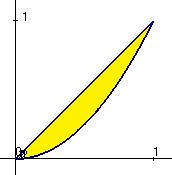
Задача 6. Найти объѐм тела, ограниченного поверхностями:

y x, y x 2 , z 0, z x 2 y 2 .

Решение. Метод построения 3-мерного чертежа: сначала выбрать все те уравнения, которые не содержат z , и построить плоскую проекцию

(вид сверху) этой фигуры. Строим графики y x, y x 2 .

Теперь видно,	что x [0,1] , а при каждом фиксированном x ,
y [x 2 , x] .	y x, y x 2 в плоскости это - уравнения кривых, но
Вообще,	y x, y x 2 в плоскости это - уравнения кривых, но

для пространства это уравнения поверхностей. Отсутствие z означает, что z любое, то есть к прямой и параболе присоединены вертикальные образующие. Представьте, что один вертикально поставленный лист ровный, а второй изогнут по параболе. Внутри такой узкой «шахты» как раз и располагается искомая фигура.

А теперь определим границы по высоте, чтобы окончательно построить чертѐж. Для каждой точки, взятой на плоскости в том основании, которое показано на предыдущем чертеже, высота

меняется от z 0 до z x 2 y 2 , эти линии отмечены зелѐным цветом. Эллиптический параболоид пересекается с каждой из

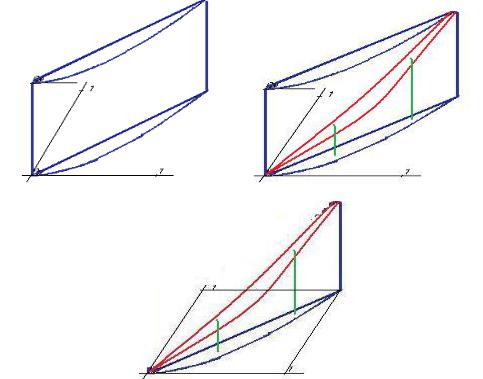
указанных ранее вертикальных стенок, пересечения показаны красным цветом.

Самая верхняя точка (1,1,2). Итак, изобразим каркас этой фигуры:

Так как вычисляется объѐм, то надо полагать																															f 1 .
1	x x2		y2												1	x											1			x
																				x	2 y2												2	y		2
																				x	2 y2												2			2
			1dz dy dx =															z		0		dy		dx =						x							dy dx =
			1dz dy dx =																	0										x
		2															2														2
0 x			0												0 x												0 x
1										3		x					1		3 4							3		6						1	4						6
1										3		x					1									3		6						1							6
	2			x			y																		x		x										3		4	x
				x

0		x y				2		3						dx =					x		x								dx =								x x					dx
				x		2											0							3			3							0 3						3
				x								x2												3
												x2

x4					x5				x7				1		1			1			1		35 21 5										9				3
x4					x5				x7				1		1			1			1		35 21 5										9				3
=													=									=								=					=			.
=													=									=								=					=			.
		3				5									3			5			21			105								105					35
		3				5			21				0		3			5			21			105								105					35
Ответ.				V				3			.
Ответ.				V			35				.
							35

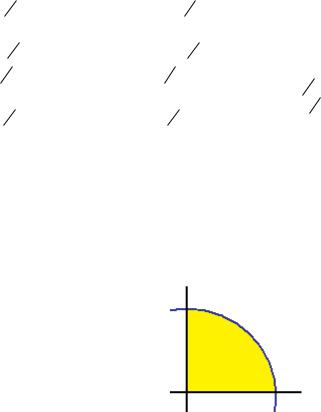
Двойные интегралы в полярных координатах.

Задача 7. Вычислить интеграл xdxdy по полукругу радиуса 1 в

правой полуплоскости.

Решение.

Алгоритм: 1) определить границы интегрирования по , .

2) пересчитать x, y в функции через , , используя x cos , y sin .

3) домножить на определитель Якоби, который равен .

Так как полукруг именно в правой полуплосости, то учитываются 4-я и 1-я четверти, то есть угол от -90 до 90 градусов.

2	1										2		1
														2
	( cos ) d d =												(	2	cos)d d =
	( cos ) d d =												(		cos)d d =
2 0												2	0

2						3	1		1	2						1				1			2
2						3	1			2
		cos						d =			cos d			=			sin	2	=		(1	( 1)) =		.
																		2

					3				3							3			2	3			3
					3				3							3			2	3			3
2			2	.			0				2
Ответ.			2
Ответ.
		3
Задача 8. Вычислить									x9 ydxdy , где D - четверть круга радиуса 1 (в
									D
первой координатной четверти).
Решение.
Заменим x cos ,									y sin , а также умножим на якобиан .

2 1												2	1
				9											11	9
( cos)					( sin ) d					d		=				cos	sin d d =
0 0												0		0
2							12	1		1		2
2							12	1				2
		9										9
	cos		sin						d =		cos		sin d
	cos		sin			12			d =	12	cos		sin d
0						12		0		12	0
0								0			0

Дальше остаѐтся интеграл от одной переменной, там можно применять обычный способ, подведение под знак дифференциала.

	1	2					1	2
	1	cos9		sin d =			1	cos9 ( sin d ) =
12		cos9		sin d =		12		cos9 ( sin d ) =
12		0				12		0
		0						0

		1	2					1 1		2		1			1
		1	cos9 d (cos ) =					1 1	cos10	2	=	1	(0 1) =		1	.
			cos9 d (cos ) =						cos10		=		(0 1) =			.
12			0					12 10		0		120		120
			0	1	.					0
Ответ.				1
Ответ.				120
				120

Домашняя задача 1. Найти объѐм тетраэдра с вершинами (0,0,0),

(1,0,0), (1,1,0), (1,1,1). Ответ. 16 .

Домашняя задача 2. Вычислить xy5 dxdy , где D - четверть круга

радиуса 2 (в первой координатной четверти). Ответ. 163 .

Решение задачи 1. Найти объѐм тетраэдра с вершинами (0,0,0),

(1,0,0), (1,1,0), (1,1,1).

Решение. Так как надо вычислить объѐм, то функция в данном случае f (x, y, z) 1 .Для того, чтобы записать интеграл, лучше сначала

нарисовать проекцию на плоскость Oxy , то есть вид сверху. Тогда мы сможем распознать границы по y в зависимости от x . А уже после

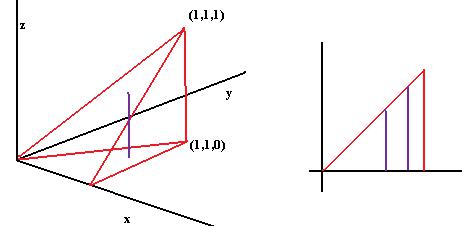
этого, для точки (x, y) выяснить границы изменения z по трѐхмерному чертежу.

Глобальные границы по x от 0 до 1. В плоской проекции видим треугольник, там границы по y в зависимости от первой переменой x

			1	x
это [0, x] . Итак, уже	можно	записать			1	dz
это [0, x] . Итак, уже	можно	записать			1	dz	dy dx . А теперь
			0	0
запишем границы по	z . От	высоты	0	до	наклонной плоскости,

уравнение которой легко может быть получено по 3 точкам (0,0,0),

Вычислим интеграл. В самой внутренней скобке, интеграл от 1 по z .

1 x			1 x	1 x
	y
z	y	dy dx =	y 0 dy dx =	ydy dx .
	0
	0
0 0			0 0	0 0

Остался уже не тройной, а двойной интеграл. Далее,

1 x		1		2	x	1	x	2			x	3	1	1

			y			=
	ydy dx =				dx		2		dx	=	6		=	6	.
0	0	0 2			0	0							0

<<< < Предыдущая 1 2 3 4 5 6 78 / 158 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023625.95 Кб06899.pdf
#
13.02.202149.22 Кб2690.pdf
#
05.02.2023505.3 Кб06905.pdf
#
05.02.2023475.83 Кб06990.pdf
#
13.02.2021815.65 Кб06OMkzBKrZ3.pdf
#
05.02.20232.15 Mб07005.pdf
#
05.02.2023618.28 Кб07014.pdf
#
05.02.2023225.21 Кб07046.pdf
#
05.02.20231.01 Mб47067.pdf
#
05.02.2023266.87 Кб17089.pdf
#
05.02.2023288.25 Кб07090.pdf