Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

7005

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

2.15 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 157 8 9 10 11 12 13 14 15 > Следующая >>>

Ответ.

Задача 5. Вычислить несобственный интеграл 1 рода

x ln 3

Решение.

d (ln x)

x ln

сделаем замену t ln x , далее

= t 3dt

t 2

1 =

Ответ.

t 2

Задача 6. Выяснить сходимость несобственного интеграла по

x3 dx

признакам сравнения: 1 x 4 2 , не вычисляя его.

Решение. В числителе степень 3, в знаменателе 4. Тогда в качестве эталонной функции, с которой надо сравнить, нужно взять такую:

g(x) x3 1 . Докажем, что с ней можно сравнивать функцию в этом x 4 x

интеграле, то есть вычислим предел их отношения и получим, что он

равен числу, а не 0 или . lim	f	lim	x3		x	= lim	x 4		= 1.

x g		x x4 2		1		x x 4 2
Это эквивалентные величины,		и сходимость				исходного		интеграла

эквивалентна сходимости интеграла . А этот интеграл

1 x

расходится, так как степень равна 1 (см. теорию). Либо это видно из того, что первообразная в данном случае лограрифм, и она не ограниченная функция.

Ответ. Расходится.

Задача 7. Выяснить сходимость несобственного интеграла по

sin x

признакам сравнения:

dx , не вычисляя его.

x3 1

Решение. Так как sin x 1, то заменив функцию

sin x

на

x3 1

sin x

получим

dx причѐм, по признаку сравнения в

x3 1

не-предельной форме, если второй интеграл сходится (обозначим его (II)), то и исходный тоже сходится. А теперь заменим на ещѐ более простую функцию, но уже по признаку сравнения в предельной форме.

Бесконечно малая величина

при

эквивалентна

x3 1

lim

Докажем это:

lim

=1.

x3 1

Поэтому сходимость интеграла

dx эквивалентна сходимости

x3 1

интеграла

dx . Обозначим его (III). А про этот интеграл уже

известно, что он сходится, ведь здесь классический случай,

рассмотренный в лекциях, а именно

dx где степень a

Итак, (III) сходится, что эквивалентно тому, что (II) сходится, а (II) > (I), поэтому исходный интеграл (I) тоже сходится.

Ответ. Сходится.

Задача 8. Выяснить сходимость несобственного интеграла по


		x 1sin x
признакам сравнения		x 1sin x		dx не вычисляя его.

	x	2	3x 5
1	x		3x 5
1

Решение. Аналогично прошлой задаче, сначала заменим на выражение без синуса с помощью неравенства, а потом перейдѐм к ещѐ более простому интегралу по предельному признаку.


		x 1sin x										x 1			x
		x 1sin x				dx						x 1	dx		x	dx , а этот интеграл равен

	x	2	3x		5				x	2	3x 5			x	2
1	x		3x		5			1	x		3x 5		1	x
1								1					1
	1						3
	1			dx ,	a		3	1,	сходится. Сходимость 2-го и 3-го эквивалентна,
	3		2	dx ,	a		2	1,	сходится. Сходимость 2-го и 3-го эквивалентна,
1 x			2				2

поэтому 2-й интеграл тоже сходится. А из сходимости 2-го следует сходимость 1-го.

Ответ. Сходится.

Задача 9. Выяснить сходимость несобственного интеграла 2-го рода

по признакам сравнения

x x2

Решение.

x x2

Особенность в 0 только у первого корня, второй там не даѐт 0 в знаменателе. Заменим на эквивалентную, в качестве которой возьмѐм функцию только с тем множителем, который стремится к 0 в

знаменателе при x 0 .

g(x)

. Докажем, что они эквивалентны:

lim

= lim

1 .

x 0

x 1 x 1

x 0

1 x

Значит,

сходится 2

сходится.

1 x

, a

1, что для интеграла 2 рода влечѐт сходимость.

0 x

0 x 2

1			1
Либо можно рассмотреть 2	dx			= 2 2	dx		12 .
	dx				dx	= 2 x
						= 2 x
0		x	0		2 x		0
							0

Ответ. Сходится.

Задача 10. Выяснить сходимость несобственного интеграла 2-го рода

cosxdx

по признакам сравнения

x sin x

Решение. Заметим, что в знаменателе x

и sin x , который в свою

очередь эквивалентен x

(по 1 замечательному пределу). Поэтому

можно взять g(x)

. Обоснуем это с помощью предела:

x 2

lim

cosx

lim cos x lim

= 1.

x sin x

x 0

x 0 x sin x

x 0

1 dx

Тогда остаѐтся выяснить сходимость интеграла 0 x 2 . Он расходится,

степень 2 > 1 что для интеграла 2-го рода влечѐт расходимость. Поэтому и исходный интеграл тоже расходится.

Ответ. Расходится.

Задача 11. Выяснить сходимость несобственного интеграла по

3 x

признакам сравнения

dx .

Решение. Это комбинированный пример на интеграл 1 и 2 рода.

Надо разбить на 2 части и исследовать отдельно окрестность 0 и

оставшуюся часть полуоси.

3 x

dx =

3 x

dx +

3 x

dx . Если S1 , S2 оба числа

конечны, то их сумма S1 S2

тоже конечна. То есть, для сходимости

надо, чтобы оба этих интеграла сходились, один интеграл 1-го рода а другой 2-го рода.

Исследуем

dx . Здесь эквивалентная величина подбирается

по самым старшим степеням, ведь надо будет найти предел в .

x 13

3 x

, тогда

lim

3 x

lim

= lim

1 .

x x2

x x 13

x x2

x 1

Интеграл

dx сходится

dx сходится. А здесь

1 x

1 , то есть он сходится.

Исследуем

dx . Здесь эквивалентная величина подбирается

по самым младшим степеням, ведь надо будет найти предел в 0.

x 13

3 x

, тогда

x 12

lim

3 x

lim

=. lim

1 .

x 0 x2

x x 13

x 0 x2

x 0 x 32 1

1				1
			3 x				1			1
Интеграл					dx сходится			dx	сходится. a		1, что
		2					1
	x		x							6
0				0		x	6

для интеграла 2 рода означает сходимость.

Итак, оба интеграла по (0,1) и (1, ) конечны, значит весь интеграл по (0, ) тоже является конечным числом.

Ответ. Сходится.

2 xdx

Задача 12. Вычислить несобственный интеграл 2 рода .

1 x2 1

Решение. Особенность в точке 1, впрочем, первообразная там может быть конечной, и мы даже не заметим, что интеграл несобственный:

2	xdx				1	2	2xdx					1	2	d (	x2 1)	2	d (x 2 1)
	xdx		=		1		2xdx				=	1		d (	x2 1)	=	d (x 2 1)	=
			=	2							=	2				=		=
1	x2 1			2		1		x 2 1				2	1		x2 1	1	2 x 2 1
Пересчѐт границ:
x 1 t 12 1 0
x 2 t 22 1 3 .
	3		dt							3 =
Далее,			dt			=			t		3 .			Ответ.		3 .

		2		t
	0	2		t						0
										0

Задача 13. Вычислить несобственный интеграл

Решение. Сделаем замену 3 x 1 t , тогда:

t (0,2) ,

x t 3

1 , dx 3t 2 dt .

Пересчѐт границ:

x 1 t 3 1 1 0

x 9 t 3 9 1 2 .

xdx

2 (t 3

3t 2 dt

= 3 (t 3 1)tdt

= 3 (t 4

x 1

9		xdx
2 рода		xdx	.
2 рода	3		.
1		x 1

t)dt =

3	t 5	2	3	t 2	2	3		3		96

					=		32		4 =		6 = 19,2 + 6 = 25,2.
5			2			5		2		5
		0			0

Ответ. 25,2.

Домашние задачи.

1		dx
Выяснить сходимость:		dx	(аналогично задаче 9).


		x x2
1		x x2
2
2		dx
Выяснить сходимость:		dx	(с разбивкой на 2 интервала в


	4x x2
0	4x x2

окрестности 0 и 2, как в задаче 11).

ПРАКТИКА № 10.

45 минут: небольшое повторение и самостоятельная (контрольная) работа на 2 задачи на 20 минут.

1. Определѐнный интеграл. 2. Несобственный интеграл. Примерные темы заданий - см. выше:

1 6x 3

Практика № 7, задача 1. Вычислить интеграл 0 x 2 1 dx .

Практика № 9, задача 2.

Вычислить несобственный интеграл 1 рода xe x dx .

Практика № 9, задача 4.

Вычислить несобственный интеграл 1 рода 0 x2 4x 8 dx .

45 минут: новая тема - двойной интеграл.

Двойные интегралы в декартовых координатах. Вычисление (задачи 1-4).

Задача 1.		Вычислить двойной интеграл xydxdy , где D
				D
прямоугольник, x [0,1], y [0,2] .
Решение. Есть эквивалентные формы записи в таком случае:
1	2	1	2
dx xydy
dx xydy		=	xydy dx . Итак, сначала во внутреннем цикле найдѐм
0	0	0	0

	1	y	2	2		1
	1		2	2		1
						= 2x dx =		2	1
первообразную по переменной	y : x				dx		x		0	= 1.
первообразную по переменной	y : x	2			dx		x		0	= 1.
	0	2		0		0
	0			0		0

Ответ. 1.

Замечание. Если изменили бы порядок интегрирования, то есть внутреннее действие по x а внешнее по y то по объѐму вычислений было бы то же самое.

2 1	2	x	2	1		2	y			y	2	2


xydx dy	= y				dy	=		dy	=				= 1.
0 0	0	2		0		0	2			4		0

Задача 2. Вычислить двойной интеграл ye xy dxdy , где D квадрат,

						D
x [0,1], y [0,1] .
Решение. У			нас	есть	2 варианта:	сделать внешний цикл по x , а
						1 1
							xy
внутренний			по	y ,	то есть	ye	xy	dy dx , либо наоборот,
внутренний			по	y ,	то есть	ye		dy dx , либо наоборот,
						0 0
1 1
	xy
ye	xy	dx dy . Несмотря на то, что область квадрат, и казалось бы,
ye		dx dy . Несмотря на то, что область квадрат, и казалось бы,
0 0

всѐ равно, каков порядок интегрирования, но если сделать внутренний цикл по y то в обоих множителях есть переменная интегрирования,

то есть мы сразу столкнѐмся с интегрированием по частям, а вот если внутренний цикл по x , то только в одном множителе есть переменная, по которой интегрируем. Более того, y служит

коэффициентом при x в степени экспоненты, то есть надо будет разделить на y , и он сократится, останется вообще одна экспонента!

Этот путь более рациональный и предпочтительно здесь сделать именно так.

1	1				1	1				1		1		1
										1

			xy						xy				xy
		ye		dx dy	= y		y	e			dy	= e		0
0		0			0		y			0		0
0		0			0					0		0
1
e y 1 dy = e y y						1 = e1 e0						(1 0)
0						0
0

	1
	= e	y	e	0	dy	=
dy	= e		e		dy	=
	0
	0

= e 2 .

Замечание. А если xe xy dxdy то наоборот, надо сделать внутренний

цикл по y , а внешний по x .

Ответ. e 2 .

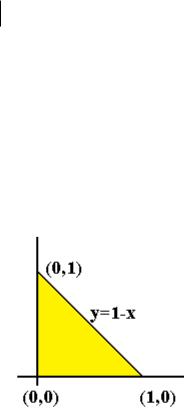
Задача 3. Вычислить интеграл (x y)dxdy по треугольнику D,

вершины которого: (0,0),(1,0),(0,1).

Решение. Строение треугольника понятно (см. чертѐж). Наклонная линия задаѐтся уравнением y 1 x .

1	1 x	1		y	2	1 x
1	1 x	1			2	1 x
			1 x
			1 x
Вычисление: dx (x y)dy = xy			0
Вычисление: dx (x y)dy = xy			0	2
0	0	0		2		0
		0				0

dx =

	1								(1 x)			2					1	2	1 2x x 2		1	1	x 2

x(1 x)										2			dx			=	x x		2	dx =		2		dx	=
	0									2							0		2		0	2	2
	x	1		x3		1		=	1		1			1	.



2		0	6			0			2	6		3
2		0	6						2	6		3

Ответ.					1		.
Ответ.							.
			3
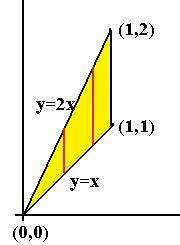
Задача 4.								Вычислить интеграл (3x 2 y)dxdy по треугольнику D,
																		D
вершины которого: (0,0),(1,1),(1,2).

Решение. Итак, по чертежу видно, что x [0,1] , а в свою очередь при каждой фиксированной абсциссе, y [x,2x].

	1	2 x	1		2 x		2	2 x

(3x 2 y)dxdy = dx (3x 2 y)dy						y
			=	3xy	x
D	0	x	0					x

dx =

<<< < Предыдущая 1 2 3 4 5 67 / 157 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023625.95 Кб06899.pdf
#
13.02.202149.22 Кб2690.pdf
#
05.02.2023505.3 Кб06905.pdf
#
05.02.2023475.83 Кб06990.pdf
#
13.02.2021815.65 Кб06OMkzBKrZ3.pdf
#
05.02.20232.15 Mб07005.pdf
#
05.02.2023618.28 Кб07014.pdf
#
05.02.2023225.21 Кб07046.pdf
#
05.02.20231.01 Mб47067.pdf
#
05.02.2023266.87 Кб17089.pdf
#
05.02.2023288.25 Кб07090.pdf